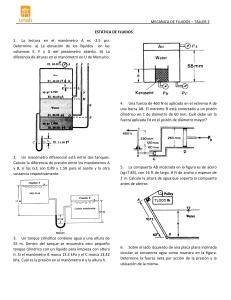
Tema 2: Fluidoestática Contenido • Ecuación de la Hidrostática • Medición de la presión • Fuerza ejercida sobre una superficie plana sumergida • Fuerza ejercida sobre una superficie curva sumergida • Principio de Arquímedes • Flotabilidad y Estabilidad UNIDAD I IM‐315 MECÁNICA DE FLUIDOS Tema 2: Fluidoestática 28 Ecuación de la Hidroestática Ecuación de la Hidroestática Del conjunto de ecuaciones anteriores: 𝑃𝑟𝑒𝑠𝑖ó𝑛 → F Fuerza→ 𝑝 𝐹 𝐴 𝐹 𝐴 𝑝 𝑤 𝑚𝑔 𝐴 𝑚𝑔 𝑚𝑎𝑠𝑎 → 𝑚 𝜌𝑉 𝑉𝑜𝑙𝑢𝑚𝑒𝑛 → V 𝐴ℎ 𝐴 · ℎ 𝜌𝑔 = h𝜌𝑔 𝐴 𝛾ℎ Consideramos un cuerpo cilíndrico para analizar el comportamiento de la diferencia de presiones con respecto a la profundidad. UNIDAD I IM‐315 MECÁNICA DE FLUIDOS Tema 2: Fluidoestática 29 Ecuación de la Hidroestática Relación de la presión y elevación Se considera un cilindro en el interior de un fluido (ambos estacionarios) A partir de la física, se sabe que para un cuerpo en equilibrio estático la suma de las fuerzas que actúan sobre el cuerpo en todas direcciones debe ser igual a cero. Aplicando equilibrio estático 𝑝 Σ𝐹𝑥 0 Σ𝐹𝑧 𝐹 Σ𝐹𝑧 Σ𝐹𝑧 Σ𝐹𝑦 𝐹 𝑤 0 𝑝 𝐴 Σ𝐹𝑧 𝑝 𝐴 0 𝜌𝑉𝑔 𝐹 ⇒𝐹 𝐴 ⇒𝑚 ⇒𝑉 𝑝𝐴 𝜌𝑉 𝐴𝑑𝑧 z A dz 𝑝 𝐴 𝑝 𝐴 𝜌𝑔𝑑𝑧𝐴 0 Por conveniencia, se define: 𝑝 𝑑𝑝 𝜌𝑔𝑑𝑧 0 𝑝 d𝑝 𝑝 𝑝 y x y d𝑧 𝑧 𝑧 ℎ 𝑑𝑝 𝜌𝑔𝑑𝑧 El signo negativo se debe al acuerdo de tomar la dirección z positiva hacia arriba, de ‐𝑑𝑝 𝜌𝑔ℎ Referencia modo que el diferencial dP es negativo cuando el diferencial dz es positivo, puesto que la presión disminuye en dirección ascendente. UNIDAD I IM‐315 MECÁNICA DE FLUIDOS Tema 2: Fluidoestática 30 Relación de la presión y elevación La presión en un fluido en reposo es independiente de la forma o sección transversal del recipiente que lo contiene. Ésta cambia con la distancia vertical, pero permanece constante en las otras direcciones. Nótese que las presiones en los puntos A, B, C, D, E, F y G son idénticos porque están a la misma profundidad interconectados por el mismo fluido estático. Sin embargo, las presiones en los puntos H e I no son iguales, porque estos dos puntos no están interconectados por el mismo fluido (es decir, no se puede trazar una curva desde el punto I hasta el H permaneciendo en el mismo fluido en todo momento), aun cuando están a igual profundidad. UNIDAD I IM‐315 MECÁNICA DE FLUIDOS Tema 2: Fluidoestática 31 Ley de Pascal Una consecuencia de que la presión en un fluido permanezca constante en la dirección horizontal consiste en que la presión aplicada a un fluido confinado aumenta la presión en toda la extensión de éste en la misma cantidad. Esto se conoce como ley de Pascal, en honor a Blaise Pascal (1623‐1662). Pascal también sabía que la fuerza aplicada por un fluido es proporcional al área superficial. Observó que se podían conectar dos cilindros hidráulicos de áreas diferentes y se podía usar el más grande para ejercer una fuerza proporcionalmente mayor que la aplicada al más pequeño. La “máquina de Pascal” ha sido la base de muchos inventos que forman parte de nuestra vida cotidiana, como los frenos y los elevadores hidráulicos. 𝑝 𝐹 𝐴 ⇒𝐹 𝐴 𝐴 𝑝 𝑝 𝐹 𝐴 𝐹 𝐴 Tema 2: Fluidoestática 𝐹 𝐹 Si la relación de área es 10. 10 𝐹 UNIDAD I IM‐315 MECÁNICA DE FLUIDOS 𝑝𝐴 32 𝐹 El Manómetro El émbolo de un dispositivo de cilindro y émbolo en posición vertical que contiene un gas tiene una masa de 60 kg y un área de la sección transversal de0.04 m2, como se muestra en la figura 3‐20. La presión atmosférica local es de 0.97 bar y la aceleración gravitacional es de 9.81 m/s2. a) Determine la presión en el interior del cilindro. b) Si se transfiere algún calor al gas y su volumen se duplica, ¿esperaría que cambiara la presión en el interior del cilindro? Σ𝐹𝑦 𝐹 𝑝 0 𝑝 𝐹 ‐𝐹 𝑊 𝑚𝑔 𝑝 A 0.97 𝑏𝑎𝑟 60 𝐾𝑔 𝐹 0 𝑝 9.81 0.04 𝑚 𝑚 ∗ 𝑠 𝐹 𝑊 𝐹 𝑝 A 𝑚𝑔 𝐴 1𝑁 1 𝑘𝑔 · 𝑚⁄𝑠 1 𝑏𝑎𝑟 10 𝑁 · 𝑁⁄𝑚 1.12 𝑏𝑎𝑟𝑠 b) El cambio de volumen no tendrá efecto en el diagrama de cuerpo libre trazado en el inciso a) y, por lo tanto, la presión en el interior del cilindro continuará siendo la misma. UNIDAD I IM‐315 MECÁNICA DE FLUIDOS Tema 2: Fluidoestática 33 El Manómetro El Manómetro: Instrumento utilizado para medir diferencias en la presión, pequeñas y moderadas. Un manómetro consta principalmente de un tubo en U de vidrio o plástico que contiene uno o más fluidos como mercurio, agua, alcohol o aceite. Bajo la acción de la presión a medir, el fluido de medición se desplaza desde su posición normal. Debido a que en el manómetro los fluidos están en reposo, se puede utilizar la ecuación 𝜟𝒑 𝜸𝒉 con el fin de escribir las expresiones correspondientes a los cambios en la presión que se producen en todo el manómetro. UNIDAD I IM‐315 MECÁNICA DE FLUIDOS Tema 2: Fluidoestática 34 El Manómetro Procedimiento para escribir la ecuación para un manómetro 1.‐ Inicie desde un extremo del manómetro. 2. Añada términos que representen los cambios en la presión usando 𝜟𝒑=𝜸𝒉 , procediendo desde el punto de partida e incluyendo cada columna de cada fluido por separado. 3. Cuando el movimiento de un punto a otro es hacia abajo, la presión aumenta y se suma el valor de 𝜟𝒑. A la inversa, cuando el movimiento de un punto al siguiente es hacia arriba, la presión disminuye y se resta 𝜟𝒑. 4. Continúe este proceso hasta que se alcance el otro punto extremo. El resultado es una expresión de la presión en ese punto final. 5. Resuelva la ecuación en forma algebraica para obtener la presión deseada en un punto dado o la diferencia de presión entre dos puntos de interés. 6. Introduzca los datos conocidos y calcule la presión deseada. (‐) (+) 𝑝 𝜌 𝑔ℎ UNIDAD I IM‐315 MECÁNICA DE FLUIDOS Tema 2: Fluidoestática 35 𝜌 𝑔ℎ 𝑝 𝑝 El Manómetro EJEMPLO El agua en un tanque se presuriza con aire y se mide la presión con un manómetro de fluidos múltiples, como se muestra en la figura. El tanque está en una montaña a una altitud de 1,400 m, donde la presión atmosférica es de 85.6 kPa. Determine la presión del aire en el tanque si h1 = 0.1 m, h2 = 0.2 m, y h3= 0.35 m. Tome las densidades del agua, el aceite y el mercurio como 1,000 kg/m3, 850 kg/m3, y 13,600 kg/m3, respectivamente Procedimiento para escribir la ecuación para un manómetro 1.‐ Inicie desde un extremo del manómetro. 2. Añada términos que representen los cambios en la presión usando 𝜟𝒑=𝜸𝒉 para cada línea de fluido. 3.La presión aumenta y se suma el valor de 𝜟𝒑, si h es hacia abajo La presión disminuye y se resta 𝜟𝒑, si h es hacia arriba. 4. Continúe este proceso hasta que se alcance el otro punto extremo. 5. Resuelva la ecuación en forma algebraica para obtener la presión deseada en un punto dado o la diferencia de presión entre dos puntos de interés. 6. Introduzca los datos conocidos y calcule la presión deseada. UNIDAD I IM‐315 MECÁNICA DE FLUIDOS Tema 2: Fluidoestática 36 El Manómetro Ejemplo 1.‐ Inicie desde un extremo del manómetro. Iniciamos en el punto 1. en la interfaz de aire‐agua 2‐3‐4 Añada términos que representen los cambios en la presión usando 𝜟𝒑=𝜸𝒉 para cada línea de fluido hasta alcanzar el punto extremos. 𝑝 +𝜌 𝑔ℎ 𝜌 𝑝 𝑝 𝜌 𝑝 𝑝 𝑔 𝜌 𝑝 𝑝 𝑔ℎ 𝑔ℎ 𝜌 𝜌 ℎ 𝑔ℎ 𝑔ℎ 𝜌 𝑝 𝑝 𝑔ℎ 𝜌 ℎ 𝜌 ℎ 𝐾𝑔 85,600 𝑃𝑎 9.81 𝑚/𝑠 13600 ∗ 0.35𝑚 𝑚 129646.9 𝑃𝑎 ≅ 130 𝐾𝑃𝑎 1000 𝐾𝑔 ∗ 0.1𝑚 𝑚 850 𝐾𝑔 ∗ 0.2𝑚 𝑚 UNIDAD I IM‐315 MECÁNICA DE FLUIDOS Tema 2: Fluidoestática 37 El Manómetro Procedimiento para escribir la ecuación para un manómetro 1.‐ Inicie desde un extremo del manómetro. 2. Añada términos que representen los cambios en la presión usando 𝜟𝒑=𝜸𝒉 para cada línea de fluido. 3.La presión aumenta y se suma el valor de 𝜟𝒑, si h es hacia abajo La presión disminuye y se resta 𝜟𝒑, si h es hacia arriba. 4. Continúe este proceso hasta que se alcance el otro punto extremo. 5. Resuelva la ecuación en forma algebraica para obtener la presión deseada en un punto dado o la diferencia de presión entre dos puntos de interés. 6. Introduzca los datos conocidos y calcule la presión deseada. UNIDAD I IM‐315 MECÁNICA DE FLUIDOS Tema 2: Fluidoestática 38