Presentación educativa Proyecto educativo Infantil Doodle Azul, amarillo, rosa y verde
Anuncio

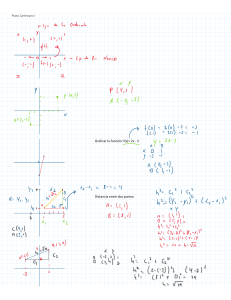
Plano Numérico Universidad: UPTAEB PNF: Sistemas De Calidad de Ambiente Nombre : Josmary Yanez Seccion : 0404 PLANO NUMÉRICO O CARTESIANO Se conoce como plano cartesiano, coordenadas cartesianas o sistema cartesiano, a dos rectas numéricas perpendiculares, una horizontal y otra vertical, que se cortan en un puntos llamado origen o punto cero. La finalidad del plano cartesiano es describir la posición o ubicación de un punto en el plano, la cual esta representada por el sistema de coordenadas. El plano cartesiano también sirve para analizar matemáticamente figuras geométricas como la parábola, la hipérbole, la línea, la circunferencia y le elipse, las cuales forman parte de la geometría analí DISTANCIA ENTRE DOS PUNTOS Permite calcular la distancia que existe entre ambos puntos, a partir de la ubicación de las coordenadas de ambos. La distancia entre dos puntos es la recta imaginaria que los une en el espacio, marcando el menor trayecto entre ambos. Esto puede darse también en el plano cartesiano o simplemente sobre la superficie terrestre. De acuerdo a cada caso, su calculo es diferente. Fórmula de distancia entre dos puntos en el plano cartesiano La distancia entre dos puntos P1 y P2 del plano se denota por d(P1, P2). La formula de la distancia usa las coordenadas de los puntos Punto Medio o Equidistante Punto medio: Es el punto que se encuentra a la misma distancia de otros dos puntos cualquiera o extremos de un segmento. Punto equidistante: Es el punto que se encuentra a la misma distancia de dos elementos geométricos, ya sean puntos, segmentos, rectas, etc. PUNTO MEDIO DE UN SEGMENTO: El punto medio del segmento AB, que llamaremos M, es un punto del segmento que dista lo mismo de A que de B. Esto quiere decir que: Si es un segmento acotado, el punto medio es el que lo divide en dos partes iguales. En ese caso, el punto medio es único y equidista de los extremos del segmento. Por cumplir esta última condición, pertenece a la mediatriz del segmento. Teorema Sea AB. Ejemplo: Un segmento cuyos extremos tienen coordenadas A(xA; yA) ; B(xB; yB) entonces las coordenadas del punto medio M(xM ; yM) de AB son: ECUACIONES Y TRAZADO DE CIRCUNFERENCIAS: ECUACIÓN DE LA CIRCUNFERENCIA: La circunferencia es el lugar geométrico de los puntos del plano que equidistan de un fijo llamado centro. DETERMINACIÓN DE UNA CIRCUNFERENCIA: Una circunferencia queda determinada cuando conocemos: a) Tres puntos de la misma, equidistantes del centro. b) El centro y el radio. €) El centro y un punto en ella. d) El centro y una recta tangente a la circunferencia. También podemos decir que la circunferencia es la línea formada por todos los puntos que están a la misma distancia de otro punto, llamado centro . Entonces, entrando en el terreno de la Geometría Analítica , (dentro del Plano Cartesiano ) diremos que — para cualquier punto, P (x, y), de una circunferencia cuyo centro es el punto C (a, b) y con radio r —, la ecuación ordinaria es (x—a)2+(y—b)2=r2 ECUACIONES DE LA PARÁBOLA: Es una forma geométrica. Esta forma geométrica, la parábola, expresada como una ecuación , cuenta con una serie de elementos o parámetros que son básicos para su descripción, y son: 1-Vértice (V) : Punto de la parábola que coincide con el eje focal (llamado también eje de simetría ). 2-Eje focal (o de simetría) (ef) : Línea recta que divide simétricamente a la parábola en dos brazos y pasa por el vértice. 3-Foco (F) : Punto fijo de referencia, que no pertenece a la parábola y que se ubica en el eje focal al interior de los brazos de la misma y a una distancia p del vértice. 4-Directriz (d) : Línea recta perpendicular al eje focal que se ubica a una distancia p del vértice y fuera de los brazos de la parábola 5-Cuerda focal : Cuerda que pasa por el foco. 6- Distancia focal _(p) : Parámetro que indica la magnitud de la distancia entre vértice y foco , así como entre vértice y directriz (ambas distancias son iguales). 7-Cuerda : Segmento de recta que une dos puntos cualesquiera, pertenecientes a la parábola. 8- Lado recto (LR): Cuerda focal que es perpendicular al eje focal. Para ilustrar las definiciones anteriores, veamos la siguiente gráfica de una parábola: Ecuaciones Elipses Se llama elipse al lugar geométrico de un plano, cuya suma de distancias a de os fijos llamados focos es constante. el lugar geométrico de los puntos P (x,y) del plano cartesiano cuya sum: las de los puntos, llamados focos: F1 y F2 es constante. Fórmula canónica: Cuando la elipse tiene forma vertical: El eje focal está paralelo al eje de las abscisas (y,y1). Cuando la elipse tiene forma horizontal: El eje focal está paralelo al eje de las abscisas (x, x1). Ecuaciones Hipérbola: Una hipérbola se define como el lugar geométrico de los puntos del plano que la diferencia de distancias a dos puntos fijos denominados focos, F y siempre constante. Las líneas azules constituyen lo que se conoce como una hipérbola. Observa sus focos F y F'. Estos puntos son muy importantes ya que la diferencia de la distancia entre cada punto P(x,y) y estos puntos es siempre constante. Por tanto, debes tener en cuenta que para cualquier punto de la hipérbola se cumple que: |d(PF)-d(P,F)|=2a Donde d(P,F) y d(P,F') es la distancia de un punto genérico P de la hipérbola al foco F y al foco F' respectivamente. Y donde 2a es una constante. Representar gráficamente las ecuaciones de las cónicas.