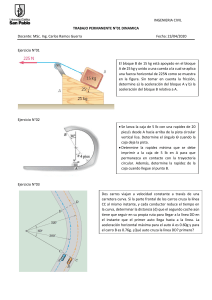
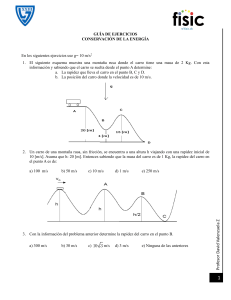
Cinética de partículas: segunda ley de Newton 12.1D Ecuaciones de movimiento Componentes tangencial y normal Componentes normal y tangencial Si una partícula se mueve a lo largo de una trayectoria curva, puede que sea conveniente utilizar componentes tangencial, normal y binormal. • • 𝐹 = 𝑚𝑎 𝐹𝑡 𝑒𝑡 + 𝐹𝑛 𝑒𝑛 + 𝐹𝑏 𝑒𝑏 = 𝑚𝑎𝑡 + 𝑚𝑎𝑛 Diagrama de cuerpo libre 1. Elija una sistema de coordenadas inercial donde denote los ejes tangencial, normal y binormal. 2. La aceleración normal actúa en el sentido positivo de la dirección normal (𝑛). 3. Si desconoce el sentido de la aceleración tangencial, asuma el sentido positivo en la dirección tangencial (𝑡). Ecuaciones de movimiento 1. Use las ecuaciones de movimiento anteriormente descritas: sumatorias en los ejes 𝑛, 𝑡 𝑦 𝑏. 𝐹𝑡 = 𝑚𝑎𝑡 𝐹𝑛 = 𝑚𝑎𝑛 𝐹𝑏 = 0 Cinemática 1. Recuerde que la aceleración tangencial y que la aceleración normal son 𝑑𝑣 𝑎𝑡 = 𝑑𝑡 𝑣2 𝑎𝑛 = 𝜌 1. Recuerde que el radio de curvatura se puede calcular utilizando Cálculo: 𝜌= 𝑑𝑦 1+ 𝑑𝑥 𝑑2𝑦 𝑑𝑥 2 2 3/2 Ejemplo 1 El carro, que tiene una masa de 1700 𝑘𝑔, viaja por una pista que tiene 20° de peralte. En el instante mostrado, el radio de curvatura de la pista es 𝜌 = 100 𝑚. Si el coeficiente de fricción estática entre las llantas y el camino es 𝜇𝑠 = 0.2: • Determine la rapidez constante máxima a la que el carro puede viajar sin resbalar hacia arriba por la pendiente. Desprecie el tamaño del carro. • Determine la rapidez constante mínima a la que el carro puede viajar sin resbalar hacia abajo por la pendiente. 𝑣𝑚𝑎𝑥 = 24.4𝑚/𝑠 𝑣𝑚𝑖𝑛 = 12.2 𝑚/𝑠 Ejemplo 2 El bloque de 6 𝑘𝑔 esta restringido a moverse a lo largo de la trayectoria parabólica lisa. El resorte restringe el movimiento, y ya que tiene un rodillo guía, este se mantiene horizontal mientras el bloque desciende. Si el resorte tiene una rigidez de 𝑘 = 10 𝑁/𝑚, y una longitud sin estirar de 0.5 𝑚, determine: • La fuerza normal sobre el bloque en el instante que 𝑥 = 1 𝑚 y el bloque tiene una rapidez de 4 𝑚/𝑠. • ¿A que tasa está incrementando su rapidez en dicho punto? (Ignore la masa del rodillo y del resorte.) 𝑁 = 11.2 N 𝑎𝑡 = 6.35 𝑚/𝑠 2 Ejemplo 3 Determine la rapidez constante de los usuarios de las sillas voladoras si se observa que los cables están tensados a un ángulo de 30° respecto a la vertical. Cada silla incluyendo al pasajero tienen una masa de 80 𝑘𝑔 . ¿Cuáles son las componentes 𝑛, 𝑡, 𝑏 de la fuerza ejercida sobre un pasajero de 50 𝑘𝑔 durante dicho movimiento? 𝑣 = 6.30 𝑚/𝑠 283 𝑁, 0, 490 𝑁 Ejercicio 1 Dos cables 𝐴𝐶 y 𝐵𝐶 están unidos a una esfera por medio de la argolla C, la cual rota con una rapidez constante formando una trayectoria circular. Determine el rango de valores de 𝑣 para los cuales ambos alambre permanecen tirantes. 3.01 𝑚/𝑠 ≤ 𝑣 ≤ 3.96 𝑚/𝑠 Ejercicio 2 • La caja de 5 𝑙𝑏 se lanza desde el punto A con una velocidad de 20 𝑓𝑡/𝑠 para que suba por la pista circular suave. Determine el ángulo 𝜃 donde la caja se despega de la pista. 112°