proporcionalidad

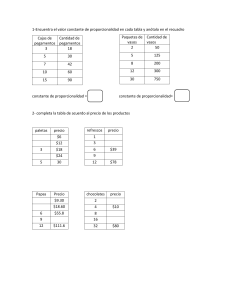
Material destinado a capacitación docente en la provincia de Santa Fe
EL PAPEL DEL PROBLEMA
EN LA CONSTRUCCIÓN
DE CONCEPTOS MATEMÁTICOS
Fragmentos:
4. LA CONSTRUCCIÓN DEL CAMPO CONCEPTUAL DE LA
PROPORCIONALIDAD DIRECTA
5. ANÁLISIS DE LA PROPUESTA GLOBAL A TRAVÉS DE UNA SECUENCIA DE
PROBLEMAS PARTICULAR, EN RELACIÓN A LA CONSTRUCCIÓN DEL
CONCEPTO DE ESCALA
ANEXO
Lic. Mabel Panizza
Lic. Patricia Sadovsky
FLACSO
MINISTERIO DE EDUCACIÓN
PROVINCIA DE SANTA FE
4. La construcción del campo conceptual de la proporcionalidad directa
Estamos acostumbrados a pensar en la proporcionalidad como un contenido escolar que se
trabaja en un determinado momento, se desarrolla, se ejercita, y se da por finalizado para pasar
al tema siguiente, que podrá ser fracciones, medida, decimales, geometría o cualquier otro que
figure entre los contenidos que debemos desarrollar.
Esta manera de planificar contempla un aspecto organizativo sin duda necesario, ya que marca
cuál va a ser el objeto específico de reflexión en cada momento del trabajo en el aula. Pero al
mismo tiempo puede hacer perder de vista el hecho de que hay un conjunto importante de
conceptos que desempeñan un papel fundamental en la adquisición del concepto de
proporcionalidad, y que esos conceptos están siendo elaborados simultáneamente con la noción
de proporcionalidad.
Efectivamente, pensar en relaciones de proporcionalidad directa nos puede remitir a situaciones
como las siguientes:
- En la librería todos los artículos están rebajados un 20%.
- Cada 2 kg de fruta se obtiene 1,5 kg de mermelada.
- El tren marcha a 100km/h.
- El plano de la casa está hecho a una escala de 1:250.
- La presión del agua bajo la superficie del mar es directamente proporcional a la
profundidad.
- Calcular cuántos paquetes de figuritas (todos iguales) es necesario comprar para tener
60 figuritas.
- Averiguar de qué material está hecho un cubo de 5 cm3 de volumen que pesa 1 kg.
Los diversos niveles de complejidad de cada una de las situaciones anteriores están dados, entre
otras cosas, por los tipos de números en juego (naturales, enteros, racionales); la naturaleza de
las magnitudes intervinientes (longitud, peso, área, volumen, peso específico, velocidad,
presión); la conceptualización acerca de la medida; la variedad de contextos de utilización; los
conceptos derivados de ciertos contextos de utilización (porcentaje, escala, velocidad, peso
específico).
Es por eso que, al plantear el problema del aprendizaje de la proporcionalidad, es necesario
tener en cuenta que la misma se inscribe en el campo de lo multiplicativo, que se trata de un
proceso complejo en el que aparece una red de conceptos relacionados unos con otros, todos los
cuales se van adquiriendo simultáneamente durante un período prolongado de tiempo. Es por
eso también que es necesario pensar en aproximaciones sucesivas al concepto de
proporcionalidad, cada una de las cuales va enriqueciendo su significado al tiempo que amplía
la comprensión de los conceptos conectados.
Para evitar ambigüedades, antes de continuar con el análisis escribiremos la definición que
hemos adoptado y las propiedades esenciales de la proporcionalidad, a las que haremos
referencia en el contexto de este trabajo. Por supuesto, el nivel de formalización con el que las
presentamos no es el que se pretende que los alumnos de la escuela primaria adquieran.
DEFINICIÓN:
Una relación de proporcionalidad directa es una relación entre dos variables, en la que el
cociente entre las cantidades que se corresponden es siempre el mismo y se denomina constante
de proporcionalidad.
2
PROPIEDADES:
1- En una situación de proporcionalidad directa, el correspondiente de un elemento a
multiplicado por un número n es igual a n por el correspondiente del número a.
a
a'
xn
xn
nxa
n x a'
2- En una situación de proporcionalidad directa, a la suma de los elementos de una de las
variables, le corresponde la suma de los correspondientes de los elementos considerados.
a
a'
+
+
b
a+b
b'
a' + b'
Abordar la complejidad que supone la apropiación del campo conceptual de la proporcionalidad
impone la necesidad de realizar un análisis tanto:
- desde la perspectiva de la estructura interna del dominio de conocimiento, como
- desde la perspectiva del sujeto que aprende.
Como se verá a través del esquema organizativo elegido en este trabajo, hemos considerado
ambos aspectos simultáneamente.
Ya hemos explicitado que adherimos a una concepción según la cual el problema juega un papel
principal en todo el proceso de aprendizaje. Es por eso que pensamos que el estudio de un
campo conceptual con intenciones didácticas debe estructurarse necesariamente a partir de los
problemas que se pueden proponer.
Como criterio general buscamos un esquema organizativo que posibilite la formulación de una
secuencia de problemas, de manera que ésta, una vez elaborada, cubra toda la complejidad del
campo conceptual y la complejidad de su adquisición.
La puesta en marcha de este criterio general adopta distintas formas según el campo conceptual
particular de que se trate. Para el caso de la proporcionalidad directa hemos adoptado un
esquema organizativo que tiene en cuenta fundamentalmente:
- los conceptos cercanos subordinados: dominio numérico (tipos de números y operaciones);
magnitudes, relación entre magnitudes; medida,
- el tipo de tarea,
- los posibles procedimientos de resolución,
- las diferentes formas de representación,
- los conceptos derivados de los contextos de utilización.
Obviamente, todos estos aspectos se interrelacionan y la complejidad de un problema particular
será producto de la interacción entre los mismos. Por ese motivo, es difícil considerar una
secuencia de problemas ordenada estrictamente por complejidad creciente. Sin embargo, del
análisis puede surgir un tratamiento exhaustivo del tema que posibilite a los alumnos establecer
la mayor cantidad de relaciones posibles a propósito del concepto de proporcionalidad.
Un análisis de este tipo se transforma en una herramienta para el docente en el momento de
seleccionar una secuencia de problemas teniendo en cuenta las características del grupo de
alumnos particular de su clase.
Estas razones justifican el tratamiento de cada aspecto particular.
3
4.1 Consideraciones acerca del esquema organizativo
•
Los conceptos cercanos subordinados
Si al encarar el estudio de la proporcionalidad los chicos dispusieran de un sólido dominio de
los distintos conjuntos numéricos y las correspondientes operaciones aritméticas en cada
conjunto, si la medida fuera un concepto totalmente elaborado, cualquiera fuera la magnitud a
medir, si pudieran considerarse adquiridas las distintas magnitudes, si los sistemas
convencionales de unidades de medida no constituyeran ningún obstáculo, tal vez el alumno
podría resolver de entrada cualquier situación de proporcionalidad aplicando la definición del
concepto.
Pero no es el caso ni podrá serlo. No es pensable la elaboración de las conceptos anteriores de
manera totalmente independiente de la elaboración del concepto de proporcionalidad directa.
Por un lado, números, operaciones, magnitudes y medidas son instrumentos para la resolución
de situaciones de proporcionalidad; y por otro, parte relevante del significado de los mismos es
obtenido por los chicos a través de la utilización de dichas situaciones.
•
El tipo de tarea
Si bien en este trabajo esperamos dejar claro que el problema es el resultado de la conjunción de
los diferentes factores que estamos analizando, pensamos que es oportuno analizar una
complejidad particular en relación al tipo de tarea involucrado.
Queremos decir con esto que aún considerando el mismo nivel de complejidad en cuanto a los
conceptos cercanos subordinados, utilizando la misma representación y siendo que el tipo de
procedimientos propicios para la resolución sea el mismo, la naturaleza de la tarea puede variar,
dando por resultado problemas de distinta complejidad. No es lo mismo, por ejemplo, completar
datos en una tabla que relacionar magnitudes directamente proporcionales, o que analizar el
significado de la constante de proporcionalidad de una relación determinada.
•
Los procedimientos posibles de resolución
Este análisis será necesariamente incompleto si no considerara los posibles procedimientos de
resolución ya que los mismos son indicadores de las conceptualizaciones alcanzadas por quienes
los ponen en práctica. Ya nos hemos referido a la manera en que los distintos procedimientos
suponen la aplicación de reglas que, correctas o no, es imprescindible tener en cuenta, ya que
muestran el estado de saber de los alumnos.
•
Las diferentes formas de representación
Tanto en la formulación de un problema como en su resolución se utilizan diferentes formas de
representación: verbal, por tablas, gráfica, por planteo, etc. Cada una de ellas resulta más o
menos favorable según la información que se desee poner de relieve.
Por otra parte, el alumno asocia a cada forma de representación determinadas tareas y
procedimientos, y en ese sentido la utilización de distintas formas aporta a ciertos aspectos
particulares de la conceptualización.
El docente que sabe que esto es así acude al uso variado de formas de representación.
En este trabajo queremos poner el acento especialmente en la importancia de ser exhaustivo en
las formas de representación, en la riqueza del análisis a partir de la integración entre las
mismas, en que el alumno sea capaz de traducir un problema de una forma a otra y en que tenga
la oportunidad de utilizar él mismo diferentes formas que por algún motivo le resulten
significativas.
En la medida en que esto se tenga en cuenta, se obtendrá como consecuencia que el alumno no
confunda el concepto con la representación. Esto debería ser – a nuestro juicio – un objetivo
importante en relación con la adquisición de conceptos.
4
• Los conceptos derivados de los contextos de utilización
Existen aplicaciones del concepto de proporcionalidad que, por tener un estatus diferenciado en
relación a otras aplicaciones, constituyen un concepto en sí mismo y en consecuencia tienen un
nombre propio. Nos referimos especialmente a: escala, porcentaje, peso específico, velocidad.
En este trabajo queremos llamar la atención sobre el hecho de que la tradición escolar ha
separado estos conceptos de la del concepto de proporcionalidad: jerarquizando los conceptos
por su nombre propio, olvidando el nombre común.
¿Qué queremos decir con esto?
Es frecuente que cuando se habla de porcentaje no se repare en el hecho de que este es un caso
particular de proporcionalidad.
Otro tanto ocurre con las reducciones dentro de un sistema de medición: no se reflexiona acerca
de que hacer una reducción significa utilizar que la medida en una longitud (por ejemplo) en una
unidad determinada, es proporcional a la medida de la misma longitud en otra unidad.
Algo análogo puede decirse en relación al concepto de escala y al de velocidad.
4.2 Análisis de problemas de proporcionalidad directa
Nos proponemos ahora analizar distintos problemas desde la perspectiva del esquema
organizativo que explicitamos en los párrafos anteriores. Queremos poner el acento en el
análisis de los problemas más que en los problemas en sí. ¿Qué queremos decir? Todas las
consideraciones que se puedan hacer, previas a la puesta de una situación en aula, enriquecen
las posibilidades de esa situación: no solamente es importante saber qué tarea van a realizar los
chicos, también es necesario anticipar qué aprendizajes harán a partir de esa tarea, qué nuevas
relaciones podrán establecer, qué distingue este trabajo del próximo y del anterior, en qué
aspectos se centrará la reflexión posterior a la resolución del problema.
Es a partir de este análisis que – esperamos – los problemas comenzarán a distinguirse unos de
otros mostrando desde lugares diferentes el concepto de proporcionalidad.
Nos ha parecido oprtuno presentar cada problema en el contexto del o los aspectos que le son
más relevantes o que le dieron sentido. Es por eso que un mismo problema puede aparecer
tratado en más de un apartado y analizado según el aspecto particular de que se trate. (Para un
listado completo de los problemas, ver anexo).
Retomamos entonces las categorías anteriores, ahora sobre los problemas concretos.
• Los problemas desde la perspectiva de los conceptos cercanos subordinados.
La naturaleza de los números y de las magnitudes: dos variables que intervienen en el asunto.
Analicemos las siguientes situaciones:
a) Paola colecciona figuritas. La siguiente tabla muestra la relación entre algunas
cantidades de paquetes y la cantidad total de figuritas que obtiene.Completar la tabla,
sabiendo que todos los paquetes traen la misma cantidad de figuritas.
Cantidad de paquetes
Cantidad de figuritas
4
20
8
2
10
100
b) Un motor consume en 4 horas 24 litros de combustible. Completar la tabla que
relaciona el tiempo de marcha del motor con la cantidad de combustible que utiliza,
sabiendo que el gasto de combustible por hora es siempre el mismo.
5
Tiempo de funcionamiento (en horas)
Combustible que consume (en litros)
4
20
8
2
10
100
Aparentemente estos problemas son casi iguales. Sin embargo la naturaleza de las magnitudes
en juego hace que el primero sea un problema planteable, sin duda, en segundo o tercer grado,
mientras que el segundo exige cierta comprensión de las magnitudes tiempo y capacidad,
comprensión que, generalmente se alcanza un poco más adelante.
Ligado a la naturaleza de las magnitudes que se relacionan en cada uno de los problemas,
aparece otro aspecto que es fundamental considerar:
- en el primer caso, si pensáramos en extender la tabla para calcular otras cantidades, o en
variar los datos iniciales, siempre estaríamos tratando con números naturales; las relaciones
establecidas hasta el momento seguramente podrán adaptarse, más o menos rápidamente, al
cálculo de nuevos valores.
- en el segundo problema, en cambio, si se introduce, por ejemplo, el cálculo del gasto de
combustible para 12 minutos de funcionamiento del motor, no alcanzarán las relaciones
establecidas hasta el momento. El chico, o bien necesitará hacer un cambio de unidades, o
bien tendrá que establecer la equivalencia:
12 minutos = 1/5 hora.
Es decir, las magnitudes del segundo problema son magnitudes continuas y los datos pueden
presentarse usando números naturales o racionales.
Una constante que varía (!)
La resolución de una situación con magnitudes continuas exige establecer una correspondencia
entre dichas magnitudes y los números que se utilizan para medirlas teniendo en cuenta una
determinada elección de las unidades de medida. Efectivamente, en el ejemplo del motor,
observamos que la constante de proporcionalidad es 5 litros por hora, es decir, es lícito pasar de
un renglón a otro de la tabla multiplicando por 5 siempre que el tiempo esté expresado en horas
y la cantidad de combustible que se consume, en litros.
Tiempo de funcionamiento
(en horas)
Combustible que consume
(en litros)
5 litros por hora
4
8
2
10
20
20
40
10
50
100
Veamos que la misma situación podrá expresarse mediante esta otra relación de
proporcionalidad directa:
Tiempo de funcionamiento
(en minutos)
Combustible que consume
(en litros)
60
120
30
1
5
10
2.5
1/12
1/12 litros por
minuto
O también por esta otra:
Tiempo de funcionamiento
(en minutos)
Combustible que consume
(en centilitros)
60
120
30
1
500
1000
250
25/3
251/3 centilitros
por minuto
Vemos entonces que para caracterizar la relación de proporcionalidad directa que describe el
gasto de combustible en función del tiempo de funcionamiento del motor es necesario fijar las
6
unidades en las que se mide cada magnitud. Este problema no se presenta cuando las
magnitudes que se relacionan no son continuas, como en el caso de las figuritas.
Moraleja:
En una situación de proporcionalidad pueden relacionarse magnitudes de la misma naturaleza
(longitudes con longitudes, por ejemplo en un problema de escalas, dinero con dinero, por
ejemplo en un problema de porcentaje) o magnitudes de distinta naturaleza (por ejemplo, tiempo
de marcha y espacio recorrido, o volumen de una sustancia y peso correspondiente). Ya sea que
se trate de una situación en la que se relacionan magnitudes de la misma o de distinta naturaleza,
corresponde analizar el problema bajo la óptica de las unidades elegidas para medir cada una de
las magnitudes, ya que la constante de proporcionalidad queda determinada por esta elección.
A veces todo cambia cuando los números cambian
Decíamos antes que consideramos pertinente establecer diferencias entre problemas, según los
conjuntos numéricos que se relacionen. Dos problemas que parecen similares porque se diferencian
solamente en el conjunto de datos, pueden ser esencialmente distintos si para un juego de datos
resulta pertinente usar el modelo de proporcionalidad directa y para el otro juego, no.
¿Qué significa esto?
Supongamos el siguiente problema:
En un bote caben 4 personas. Completar la tabla que relaciona cantidad de botes con
cantidad de personas, sabiendo que todos los botes utilizan al máximo su capacidad.
Si la tabla a completar fuera ésta:
Cantidad de botes
Cantidad de personas
1
4
2
3
24
40
Es decir, si admitimos que la cantidad de personas sea múltiplo de 4, la relación planteada es de
proporcionalidad directa.
Si en cambio proponemos esta tabla:
Cantidad de botes
Cantidad de personas
1
4
5
6
7
8
9
Es decir, si admitimos que la cantidad de personas puede ser cualquiera, la situación deja de ser
una situación de proporcionalidad. (Ya no se puede pasar de un renglón a otro de la tabla
multiplicando por una constante).
Este ejemplo apunta a marcar una cuestión que suele pasar inadvertida: la lógica interna de las
relaciones de proporcionalidad hace relevante la consideración de los conjuntos numéricos que
se relacionan. En ese sentido, este ejemplo es diferente de los que propusimos en párrafos
anteriores ya que en aquellos casos hacíamos la distinción apuntando fundamentalmente a la
complejidad psicológica que supone operar con distintos conjuntos numéricos.
Continuando con el análisis de las diferencias cualitativas que pueden ofrecerse cambiando el
juego de datos, consideremos el siguiente problema:
En séptimo A, 4 de cada 7 alumnos concurren al viaje de egresados. En séptimo B
concurren al viaje 5 de cada 8. ¿En cuál de los dos cursos es mayor la proporción de
alumnos que concurren, respecto del total de alumnos de la clase?
Observemos que no se pregunta en cuál de los dos cursos viajarán más alumnos (pregunta que
no se podrá responder con los datos del problema, ya que se desconoce el total de alumnos de
cada curso).
7
La idea es establecer comparaciones a partir de medir la relación parte-todo en cada uno de los
grupos. Esto no es trivial en absoluto y sólo podrá elaborarse si los alumnos tienen la
oportunidad de enfrentarse con situaciones de este tipo.
Veamos las tablas que resultarán de considerar, para ambos séptimos, determinadas cantidades
de alumnos en el curso:
SÉPTIMO A
Si la cantidad de alumnos del curso fuera
La cantidad de alumnos viajantes sería
7
4
14
8
21
12
28
16
SÉPTIMO B
Si la cantidad de alumnos del curso fuera
La cantidad de alumnos viajantes sería
8
5
16
10
24
15
32
20
Notemos que el significado de la constante de proporcionalidad es mucho más abstracto que en
todos los casos anteriores: para séptimo A, por ejemplo, es 4/7, y significa que los cuatro
séptimos de la división viajan. Acá aparece otra relación que los alumnos deberán establecer:
decir que los 4/7 del curso viajan es lo mismo que decir que de cada 7 chicos, 4 viajan.
Este ejemplo propone una relación de proporcionalidad directa en la que los conjuntos que se
vinculan se expresan numéricamente con números naturales y la constante de proporcionalidad
es un número racional. Observemos que la consideración – para el caso de la razón 4/7 – de una
cantidad de alumnos que no sea múltiplo de 7, pierde sentido en la realidad.
Cabe destacar que, a través de este problema, es posible enriquecer el significado de los
números racionales. Vemos entonces cómo la construcción del concepto de proporcionalidad
aparece imbricada con las sucesivas ampliaciones de los conjuntos numéricos, a tal punto que
ambas elaboraciones se nutren una a la otra.
Cuando se trata de tomar parte
Comparemos ahora esta situación:
Cuatro de cada siete alumnos irán al viaje.
con esta otra:
Para obtener la proporción óptima, mezclar siete partes de barniz con cuatro partes
de aguarrás.
Estas dos situaciones suelen confundirse aunque son completamente diferentes. La primera es
equivalente a expresar "los 4/7 del curso irán de viaje". En el segundo caso, en cambio, la razón
4/7 no está expresando una relación parte-todo, sino la relación entre las partes de barniz y las
partes de aguarrás. Si quisiéramos expresar la parte de aguarrás que contiene la mezcla
tendríamos que usar la fracción 4/11.
En general, la comparación de dos situaciones de proporcionalidad hace poner en juego –
explícita o implícitamente – series de razones iguales que es necesario comparar.
En síntesis:
Todo este punto que analiza los problemas desde la perspectiva de los conceptos involucrados,
intenta establecer diferencias según la naturaleza de los números que intervienen y de las
magnitudes que se relacionan. Diferenciamos los problemas según:
- los conjuntos que se relacionan se representen por números naturales o recionales,
- la constante de proporcionalidad de la relación sea un número natural o racional,
- las magnitudes que se relacionan sean o no de la misma naturaleza.
8
• Los problemas desde la perspectiva del tipo de tarea
En este apartado analizaremos cierto tipo de complejidad que se relaciona específicamente con
la tarea pedida, en la medida en que es posible separarla de la complejidad que aportan los otros
elementos en la conformación de un problema.
Dos problemas pueden ser idénticos desde el punto de vista de quien posee todas las estrategias
del pensamiento adulto y es experto en el dominio de conocimiento, y ser muy distintos desde el
punto de vista del sujeto que aprende (Álvarez, Panizza, 1989).
Analicemos ahora algunos aspectos que pueden dar lugar a diferentes niveles de complejidad y
que consideramos importante tener en cuenta a la hora de formular problemas de
proporcionalidad.
El lugar de la incógnita en el enunciado verbal
Consideremos los siguientes problemas:
Si 4 paquetes tienen 20 caramelos, ¿cuántos caramelos hay en 12 paquetes?
Si 4 paquetes tienen 20 caramelos, ¿cuántos paquetes necesito para tener 60 caramelos?
Ambos problemas requieren del mismo concepto y están presentados de la misma manera
(verbalmente). Sin embargo, para su resolución es posible que el alumno diga inmediatamente
para el primer problema:
4 p ----- 20 c
12 p -----
x
y resuelva.
Para el segundo de estos problemas, en cambio, el alumno deberá reconocer previamente que
más allá del orden en que se relacionen los datos y la incógnita en el enunciado, se trata de una
regla de tres simple.
Es evidente que, una vez entendido esto, se trata de resolverlo por cualquiera de los
procedimientos correctos. El hecho de que ambos problemas sean realmente distintos para el
alumno es justamente ese análisis previo, y agrega una complejidad importante en comparación
con el primer problema.
Comparar situaciones, comparar constantes
Problema:
Don Francisco y don Tomás venden las figuritas que colecciona Paola. En el quiosco
de don Francisco, el precio de 5 paquetes es de $ 3,5. En lo de don Tomás el importe
de 8 paquetes asciende a $6. ¿En cuál de los dos quioscos es menor el precio de un
paquete?
En este problema se propone como tarea la comparación de los precios unitarios. Dicho en
términos matemáticos, se pide la comparación de las constantes de proporcionalidad
correspondientes a ambos quiosqueros.
Observemos que, para cada relación, se da como dato un solo par: cantidad de figuritas – precio
correspondiente, y ninguno de los dos pares contiene el precio de 1 paquete.
La complejidad del problema es mayor que la que supone completar una tabla de
proporcionalidad: es necesario acá comparar las razones 3,5/5 y 6/8 que corresponden al precio
de un paquete en cada quiosco.
Supongamos ahora que el problema hubiera venido formulado de manera tal que la pregunta
fuera:
¿En cuál de los dos quioscos convendrá comprar?
9
Si bien este problema no puede considerarse mucho más complejo que el anterior, sí supone una
tarea, por lo menos, más extensa. El alumno podrá pensar en resolverlo calculando el precio
unitario (es decir reduciendo el problema al problema anterior), o podrá comparar el precio de
una determinada cantidad (5, 8, 10 o lo que le resulte conveniente) para comparar. (Veremos
este tipo de alternativas en c) Procedimientos posibles de resolución.)
En ambos problemas deberá manejar simultáneamente dos relaciones de proporcionalidad, lo
que representa una complejidad mucho mayor que completar una tabla. A esto se le agrega una
complejidad adicional, si en vez de pedir el cálculo del valor unitario, el alumno debe elegir esa
tarea o alguna otra que le permita comparar.
Cuando la comparación de constantes se complica
Notemos que en el ejemplo de los quiosqueros, en cada relación, una de las magnitudes que
interviene se expresa numéricamente con números naturales (cantidad de figuritas). La misma
situación de comparar las constantes puede complicarse aún más si las dos magnitudes que se
relacionan son continuas, como por ejemplo en el siguiente problema
Un jabón en polvo viene en paquetes de 500 gramos a $ 3,70 o en paquetes de 300
gramos a $ 2,10. ¿Cuál de los dos envases resulta más económico?
Acá, la búsqueda de la constante se dificulta por el hecho de que el valor correspondiente a 1
gramo de jabón carece de sentido en la realidad. Retomaremos este ejemplo cuando analicemos
procedimientos posibles.
De paso, invitamos al lector a volver a analizar en este nuevo contexto el problema de los
alumnos que viajan según la proporción y el número de cursos. (Véase la sección Todo cambia
cuando los números cambian.)
¿Dónde está la pregunta?
Consideremos ahora los siguientes problemas:
A- Laura estuvo haciendo un plano para su departamento: un ambiente, cocina, baño,
y un hall de entrada. Completar la siguiente tabla, sabiendo que con 1 cm va a
representar 1 m (o sea con una escala de 1cm / m):
Habitación
Baño
Cocina
Hall
Medida real
(en metros)
Medida sobre el plano
(en cm)
Largo
4
.........
Ancho
3,50
.........
Lado
1,50
.........
Largo
3
.........
Ancho
2,50
.........
Lado
1
.........
B- Al fin se decidió por otra escala. El lado del baño quedó sobre el plano, de 3 cm.
¿Qué escala utilizó esta vez? ¿Por qué?
C- Entusiasmada agregó un balcón terraza a su último plano. Le quedó así:
¿Qué medidas sueña para su balcón?
10
Este conjunto de problemas plantea exhaustivamente el tratamiento del lugar de la meta y del
dato en una tabla de proporcionalidad. Analizando los enunciados queda claro que se trata de:
a) Dadas la escala y las medidas reales, obtener las medidas en el plano (problema A).
b) Dadas las medidas reales y las del plano obtener la escala (problema B).
c) Dadas la escala y la medida en el plano obtener la medida real (problema C).
En esta secuencia, hemos planteado distintos tipos de tareas:
- Búsqueda de incógnitas que pueden pertenecer a cualquiera de los dos conjuntos que se
relacionan.
- Análisis del significado de la constante de proporcionalidad en una situación particular.
- Comparación de situaciones similares a partir del análisis de las respectivas constantes de
proporcionalidad.
Por último pero no menos importante, consideremos este problema, que merece una atención
especial:
Laura tomó un mapa y sacó una fotocopia reducida del mismo. Aquí está:
El mapa original
estaba perfecto,
pero la fotocopia
contiene un
error. ¿Cuál es?
Este es el problema más complejo de la serie, y requiere poner en juego un alto poder de
conceptualización. Por otra parte, su resolución no puede hacerse mediante una cuenta, sino que
requiere hacer un razonamiento sobre datos que no son numéricos.
El alumno podrá resolverlo, por ejemplo, analizando el significado de que tanto en el mapa
original como en la fotocopia 1 centímetro representa 25.000.000 centímetros (escala 1:
25.000.000), y llegar entonces a una contradicción. Este es un razonamiento que utiliza
números, pero que los números utilizados sean considerados como datos relevantes requiere un
análisis de la información que no es trivial:
- El alumno debe seleccionar entre toda la información que da el enunciado (en el que
interactúan la información gráfica y la verbal), aquella que resulte pertinente para
responder.
- No son los números en sí mismos los que constituyen la información pertinente, sino una
relación entre los mismos.
Hemos observado que muchos alumnos intentan resolver el problema utilizando información no
relevante. Resulta para ellos un proceso sumamente fructífero ir descartando soluciones
11
incorrectas a medida que avanzan en el análisis de la situación. Aún en el caso de que el alumno
llegue a la resolución correcta sólo con ayuda del docente, el abordaje de este problema da lugar
a conceptualizaciones importantes.
Resulta interesante en este problema observar que la escala está presentada en dos formas:
numérica y gráfica. Como ya dijimos, el alumno deberá llegar a la conclusión de que la escala
numérica (1: 25.000.000) es errónea (con esto responde el problema). Pero además el maestro
puede hacer observar que la escala gráfica no cambia a pesar de la reducción, ya que la misma
también es “víctima” de la misma reducción que sufre el resto de la figura.
Si se ubica este problema después de los problemas anteriores de escala, los chicos podrán
relacionar las conclusiones establecidas anteriormente con esta nueva situación: al reducir la
figura cambia la escala utilizada. Esta es una conclusión de un nivel de complejidad superior a
las obtenidas anteriormente, y de alguna manera le da un significado más rico al concepto ya
elaborado.
Deseamos a propósito de este problema, y en particular de esto último que acabamos de señalar,
llamar a una reflexión de orden teórico: el alumno, para resolver el problema, buscará dentro de
sus recursos alguno que lo ayude, pero seguramente necesitará algún recurso nuevo, no utilizado
hasta el momento. En ese sentido decimos que no aplicará (estrictamente) lo aprendido, sino que
realizará un proceso que enriquecerá el conocimiento anterior.
Según nuestra concepción, la idea de aplicación es relativa al estado de conocimiento de quien
la realiza. Desde el punto de vista de quien ya ha elaborado el concepto puede hablarse de una
aplicación propiamente dicha, que se corresponde con que el concepto utilizado se encuentra en
estado acabado, y se trata de aplicarlo en un contexto particular. Desde el punto de vista del
alumno, el término aplicación se relativiza, porque el problema apunta a construir el significado
de la proporcionalidad, a partir de proveer un contexto complejo en el cual no cabe una
utilización mecánica del concepto acabado.
•
Los problemas desde los posibles procedimientos de resolución
Nos interesa ahora mirar los problemas desde la óptica de los posibles procedimientos de
resolución. Pensamos que es necesario facilitar, desde los problemas que se proponen, el mayor
despliegue posible de estrategias.
Para el análisis de los posibles procedimientos de resolución será especialmente relevante tener
en cuenta la definición del concepto de proporcionalidad directa y las propiedades derivadas de
dicha definición.
¿En qué sentido es pertinente tener en cuenta estos aspectos? La consideración de la definición
y de las propiedades fundamenta los distintos procedimientos que se ponen en juego ante la
resolución de una solución concreta.
Analicemos nuevamente el problema de Paola y las figuritas, ahora centrados en las estrategias
para su resolución. Recordémoslo:
Paola colecciona figuritas. La siguiente tabla muestra la relación entre algunas
cantidades de paquetes y la cantidad total de figuritas que obtiene. Completar la
tabla, sabiendo que todos los paquetes traen la misma cantidad de figuritas.
Cantidad de paquetes
Cantidad de figuritas
4
20
8
2
10
100
Para el cálculo de la cantidad de figuritas de 8 paquetes, hemos observado que la estrategia más
frecuente que los niños ponen en juego (siempre que se les permita producir sus propias
x2
estrategias) es multiplicar 20 x 2.
Cantidad de paquetes
Cantidad de figuritas
4
20
8
40
x2
12
Cuando se solicita a los niños que fundamenten su procedimiento, en general dicen que cosas
como ésta:
"que hay que hacer 20 x 2 porque si tengo el doble de paquetes, voy a tener el doble de
figuritas".
Observemos que el argumento de los chicos es una primera versión de la propiedad 1, que
hemos enunciado en la página 2.
Es que justamente los chicos conocerán la propiedad a través de un proceso de construcción que
pasará por distintas instancias hasta llegar a su elaboración acabada. Así, es probable que
primero haya un uso implícito de la propiedad, que podrá explicitarse en un debate con todo el
grupo de clase, coordinado por el docente.
Es probable también que en un principio los chicos usen la propiedad en el caso de que haya que
duplicar, pero que no la pongan en juego si se trata de hacer otra multiplicación. La validez de la
propiedad para otros números distintos de 2 se irá extendiendo progresivamente a través de la
resolución de problemas, de la reflexión alrededor de los mismos, de la posibilidad de
confrontar estrategias con otros compañeros, ...
Aplicando la misma propiedad se puede calcular la cantidad de figuritas que hay en 2 paquetes:
:2
Cantidad de paquetes
Cantidad de figuritas
4
20
2
10
:2
Un procedimiento posible para calcular las figuritas correspondientes a 10 paquetes es hacer
40 + 10. Claro, se fundamenta en la propiedad de la suma (propiedad 2 de la página 2).
:2
8+2
x2
Cantidad de paquetes
Cantidad de figuritas
4
20
8
40
2
10
10
50
x2
10 + 20
:2
En la tabla siguiente mostramos posibles procedimientos para el cálculo de las otras incógnitas:
:2
x2
8+2
x2
Cantidad de paquetes
Cantidad de figuritas
4
20
4 + 20
:2
8
(40)
2
(10)
10
(50)
5
(25)
1
...
(20)
100
...
120
:2
x2
:2
10 + 40
+
20 + 100
x2
13
El famoso cálculo de la unidad
El cálculo de la cantidad de figuritas de 1 paquete se puede pensar de varias maneras. Una de las
cuentas que resuelve el asunto en el caso de Paola y sus figuritas es:
20 / 4 = 5
Esta cuenta corresponde en realidad a dos maneras distintas de pensar en la cuestión:
1) Como 1 es la cuarta parte de 4, entonces en 1 paquete hay la cuarta parte de figuritas que en
4 paquetes, es decir que en 1 paquete hay 20/4 = 5 figuritas. (Aplicación de la propiedad 1
pág. 24)
:4
Cantidad de paquetes
Cantidad de figuritas
4
20
1
5
:4
2) El cociente entre las cantidades que se corresponden es siempre el mismo y es la cantidad
de figuritas por paquete. (Aplicación de la definición).
20 figuitas
= 5 figuritas por paquete
4 paquetes
Aunque en los dos procedimientos descriptos la cuenta es la misma, las relaciones establecidas
para llegar a esa cuenta no son iguales:
En el primer caso, las dos magnitudes que se relacionan se manejan independientemente una de
otra. En el segundo procedimiento, en cambio, se introduce una magnitud cociente: la cantidad
de figuritas por paquete.
Una tercera manera de calcular la cantidad de figuritas que hay en un paquete se obtiene
haciendo 25 – 20.
¿Cuál es la relación que lleva a esta última cuenta? Si en 4 paquetes hay 20 figuritas y en 5
paquetes hay 25, a la diferencia de paquetes, que es 1, corresponde la diferencia de figuritas
que es 5.
Vemos entonces que no hay una única manera de reducir a la unidad, tal como supone la
tradición escolar en materia de procedimientos.
¿Es imprescindible “pasar de la unidad” para plantear relaciones multiplicativas?
Necesidad de operar con fracciones
Analicemos ahora el siguiente problema
Laura, Aníbal y Julieta se pusieron de acuerdo: al terminar la fiesta dividirían el resto de
la torta en tres partes iguales: una para cada chico. Completar la siguiente tabla, que
relaciona la fracción que recibirá cada chico con algunos posibles restos de torta:
fracción de torta restante
1/2
1/3
1/4
...
fracción para cada chico
...
...
...
1/4
14
En este problema los datos que se proponen son números racionales y la constante de
proporcionalidad también es un número racional: 1/3. Es evidente que en este caso es mucho
más difícil aplicar las relaciones de tipo “a doble, doble”; “a mitad, mitad”; o “a la suma, la
suma”. Para el alumno no es tan claro que, por ejemplo, 1/4 es la mitad de 1/2. El dominio de
validez de estas propiedades no se extiende tan fácilmente de los naturales a los racionales. Este
hecho puede hacer que los alumnos busquen otras relaciones entre los elementos de la tabla y
descubran que es bastante económico multiplicar por 1/3 o por 3 según donde se encuentre la
incógnita.
En la medida en que un cambio en los datos numéricos implica un cambio en los
procedimientos que produce el alumno, el docente puede manejar esta variable para bloquear o
favorecer determinadas estrategias.
Distintos procedimientos a propósito de la tarea de comparar relaciones.
Ya nos hemos referido al problema 3 del anexo. Se trata en este caso de comparar dos relaciones
de proporcionalidad directa.
Vimos que una manera de resolver la situación es comparar las respectivas constantes de
proporcionalidad.
Queríamos llamar la atención respecto de otras estrategias posibles:
Francisco
cantidad de
precio
paquetes
x4
5
3,5
20
14
Tomás
cantidad de
precio
paquetes
x4
x2
:4
8
6
16
12
4
+
20
+
3
x2
:4
15
La comparación es posible si se igualan, o bien la cantidad de paquetes, o bien los precios. La
intención de mostrar otros procedimientos es señalar hasta qué punto el aferrarse a
procedimientos convencionales puede trabar las posibilidades de enriquecimiento de la
conceptualización.
Conclusiones:
A manera de síntesis queremos destacar las siguientes cuestiones:
- la diversidad de procedimientos en el aula, junto con el intercambio de los mismos entre los
compañeros constituyen factores de progreso en el conocimiento. El alumno amplía su
propia comprensión tanto cuando necesita encontrar palabras para explicar sus
producciones, como cuando debe centrarse en el punto de vista de otro alumno;
- la utilización de uno u otro procedimiento por parte del alumno debiera atender a las
características de la situación y a razones de economía;
- los problemas de regla de tres son problemas de proporcionalidad directa en los que se da
un par de elementos que se relacionan y se pide hallar el correspondiente de otro elemento.
No hay nada que justifique su tratamiento separado de la proporcionalidad;
- el docente puede propiciar o bloquear determinados procedimientos a partir de variar los
datos de los problemas que propone.
15
•
Los problemas desde la perspectiva de la utilización de diferentes formas de representación.
En este trabajo queremos poner el acento especialmente en la importancia de ser exhaustivo en
las formas de representación, en la riqueza del análisis a partir de la integración entre las
mismas, y en que el alumno sea capaz de traducir un problema de una forma a otra.
En la medida que esto se lleve a cabo, se obtendrá como consecuencia que el alumno no
identifique el concepto con la representación. Esto deberá ser – a nuestro juicio – un objetivo
importante en relación a la adquisición de conceptos.
Cada forma de representación pone de relieve un aspecto de la información que se provee o se
maneja. Por ejemplo, el grafico cartesiano permite visualizar globalmente el comportamiento de
la relación, será especialmente relevante cuando interese comparar dos relaciones se describen
fenómenos semejantes. La tabla de datos, a su vez, es propicia para la puesta en juego de las
propiedades 1 y 2 de la proporcionalidad.
Por otra parte, el alumno asocia a cada forma de representación determinadas tareas y
procedimientos, y en ese sentido la utilización de distintas formas aporta a ciertos aspectos
particulares de la conceptualización.
Asimismo, cada forma tiene su complejidad particular.
Es habitual que ante problemas presentados en forma análoga al problema 2 del Anexo, el
alumno mire la tabla y asocie inmediatamente la situación con una de proporcionalidad, aún
antes de haber leído la parte de formulación verbal del problema, que justificaría que la
asociación es correcta.
¿Por qué motivo ocurre esto? La explicación es sencilla. Los alumnos asocian tareas y
conceptos con las representaciones habituales propuestas por sus maestros (o por situaciones no
escolares). De esta manera, la resolución del problema puede transformarse en una aplicación
mecánica de algunos métodos aprendidos en relación al concepto. En este caso, la respuesta será
correcta. Pero, podemos hablar de resolución correcta? Pensamos que sí solo en la medida en
que el alumno haya analizado la totalidad del enunciado, y sepa que se trata de una situación de
proporcionalidad a partir de un análisis crítico de la situación.
Ese sentido crítico se desarrolla a partir de ejercitar al alumno en la discriminación entre
concepto y representación.
Consideremos los siguientes problemas:
A. Completar la siguiente tabla:
Edad de Aníbal
11
12
23
Edad de Laura
14
B. Uno de estos cuadros, corresponde a cantidades que no son directamente
proporcionales ¿Cuál es? ¿Por qué?
2
4
6
4
8
12
2
4
6
4
8
9
Ambos utilizan la representación tablas, pero en el problema A no hay proporcionalidad, y en el
B se trata de discriminar en caso en que sí lo es de otro en que no.
Apuntamos con esto a la independencia entre la forma de representación y el concepto.
16
Consideremos ahora este otro problema
Paola colecciona figuritas. Cada paquete trae 5 figuritas. ¿Cuántas figuritas podrá pegar
en su álbum si compra 8 paquetes?
Allí se utiliza una formulación estrictamente verbal, con una estructura que puede asociarse
nuevamente con la proporcionalidad, por el hecho de que la mayor parte de los problemas dados
verbalmente en la escuela para utilizar proporcionalidad, son dados de esa manera.
Una aplicación del modelo de proporcionalidad llevará en este caso a una respuesta errónea. Si
el alumno respondiera desde el sentido común, desde su enorme experiencia con figuritas,
seguramente no se equivocaría: cualquier chico sabe que al comprar varios paquetes, las
figuritas se repiten y no podrá pegarlas todas en su álbum. Por lo tanto no tiene sentido decir
que comprando 8 paquetes, podrá pegar 40 figuritas. Es probable que el docente se equivoque es
ese sentido más que el alumno, si se apura a responder el problema sin analizarlo. Por ese
motivo nos ha parecido oportuno incluirlo aquí:
- Por un lado, si el docente, apurado, realiza la operación 5x8, habrá experimentado lo que
significa asociar una forma de representación con el concepto, y podrá reflexionar acerca
de las consecuencias didácticas de este hecho. Invitamos al lector a compartir su
experiencia con otros colegas, cualquiera haya sido su situación frente al problema.
Seguramente encontrará algún colega que no haya tomado la precaución de analizar las
condiciones antes de responder (entre otras cosas porque el problema parece demasiado
fácil).
- Por otro lado, para el chico, el problema es muy claro para entender por qué no se puede
multiplicar 5x8, dado que es un problema muy significativo para él. De esa manera,
resultará natural discutir con él y conjeturar las condiciones que deben cumplirse para
hablar de proporcionalidad. Se estará apuntando entonces a establecer las condiciones de
aplicabilidad del modelo ( por supuesto, no queremos decir con esto que haya que decirlo
en estos términos al hablar con el alumno).
Otro punto importante se refiere al trabajo que el alumno debe hacer cuando pasa de una forma
de representación a otra. Nuevamente, los problemas 15 a 19, y el problema 20 acuden a
auxiliarnos.
El problema 15 tiene una parte formulada verbalmente y otra en forma de tabla. Se trata de
utilizar la constante de proporcionalidad (dada verbalmente) para completar la tabla.
El problema 16, en cambio, requiere que el alumnos construya una tabla (u otra forma de
representación) para analizar las medidas correspondientes con cada una de las escalas.
Otro tanto ocurre con el problema 17, esta vez para averiguar las medidas reales.
Los problemas 18 y 20 presentan la información de manera gráfica. El alumno deberá buscar los
datos relevantes a partir del mismo, y utilizar alguna forma de representación a fin de
resolverlos.
El conjunto total de problemas está pensado para poner en juego distintas formas de
representación y posibilitar la interacción entre las mismas.
•
Los problemas desde la perspectiva de los conceptos derivados de contextos particulares
de utilización
Velocidad
Ya nos hemos explayado acerca de la dificultad que tiene para el alumno el uso de la
proporcionalidad cuando se relacionan magnitudes. La comparación de velocidades medidas
17
con distintas unidades requiere poner en juego esta dificultad, a través de sugerir la necesidad de
llevar a la misma unidad (cociente) los valores, a fin de compararlos.
Esta es la intención del problema 13. El enunciado pretende ser impactante en el hecho de que
los números involucrados, 120, 2, 2000 y 120000, que representan ciertas velocidades medidas
en distintas unidades, parecen sugerir un orden entre dichas velocidades, pero la sugerencia es
engañosa.
Cuando el alumno lleva dichas medidas a una unidad común (criterio que debería desarrollar
por sí mismo) llega a la conclusión de que todas las velocidades son iguales. La sugerencia es
que este problema promueva una discusión sobre el significado de las unidades y sobre el hecho
de que la constante de proporcionalidad depende en realidad de las unidades en juego: al
cambiar las unidades, la constante cambia (por ejemplo si se lleva todo a km/h, resulta para
todas las situaciones que la constante es igual a 120). Insistimos en esto por el hecho de que la
palabra constante tiene una connotación demasiado poderosa en el sentido de no variar Que el
alumno entienda en qué sentido no varía es un aspecto que puede llevar bastante tiempo. Si no
se le presentan problemas que pongan en juego esta (aparente) contradicción puede que el
alumno no reflexione nunca acerca de ello.
El problema 14 tiene una formulación abierta. La idea es que el alumno ponga en juego el
concepto de velocidad a partir de la necesidad de medirla. Deberá para ello establecer relaciones
pertinentes. Podrá por ejemplo registrar el espacio recorrido en varios períodos de tiempo de la
misma duración u observar el tiempo que tarda en recorrer determinada cantidad de camino.
La reducción de una unidad a otra.
El problema siguiente es un viejo conocido de la tradición escolar:
Completar la siguiente tabla que expresa la relación entre la cantidad de kilómetros y la cantidad
de centímetros contenidos en determinadas longitudes.
Cantidad de kilómetros
1
Cantidad de centímetros
....
2
…
0,02
….
…
1
Lo hemos incluido aquí con el ánimo de hacer la reflexión de que la medida de una longitud en
una unidad determinada es proporcional a la medida de esa misma longitud en otra unidad. Esto
es un concepto muy poderoso sobre el cual usualmente no se reflexiona.
Es habitual que los chicos digan: las medidas de longitud van de 10 en 10. Invitamos a que
hagan la experiencia de preguntarles qué significa eso de que van de 10 en 10. Este es un
ejemplo especialmente claro en relación a la fragmentación del conocimiento al que ya nos
hemos referido: al considerárselo un tema en sí mismo se lo ha desvinculado del concepto de
proporcionalidad. Esto va en contra de la búsqueda de conceptualización por parte de los
alumnos.
5. Análisis de la propuesta global a través de una secuencia de problemas
particular, en relación a la construcción del concepto de escala
Hasta aquí hemos realizado un detallado análisis de las distintas variables que pueden influir en
la complejidad de un problema. Como anunciáramos al principio, un problema particular es la
conjunción de todos esos factores: conceptos subordinados, tipo de tarea, procedimientos
18
sugeridos, formas de representación y, si corresponde, conceptos derivados de los contextos de
utilización.
Esperamos hasta aquí haber logrado transmitir un método de análisis de los problemas o
conjunto de problemas a fin de que sirva para que el docente elija una secuencia apropiada para
cada situación didáctica particular, que tenga en cuenta las características de su grupo de
alumnos.
A manera de síntesis, presentamos aquí un conjunto de problemas que, en el contexto particular
del concepto de escala, contiene la combinación de los distintos factores analizados, con niveles
crecientes de complejidad.
Los problemas a los que hacemos referencia figuran en el anexo como problemas número 15,
16, 17, 18, 19, 20 y 23.
No realizaremos en este contexto el análisis de aspectos que ya hemos analizado anteriormente.
Sí nos interesa llamar la atención sobre cuáles de ellos están presentes.
En primer lugar, en los problemas 15 a 20, se ve una forma de trabajar exhaustivamente los
tipos de tarea que se pueden proponer. Cada uno de ellos pone en juego una estrategia diferente,
en relación a cuáles son los datos y cuál la meta. Por supuesto, este tratamiento puede (y
sugerimos que se haga) hacerse con cualquier problema. Sin embargo, nos parece especialmente
interesante en el caso de las escalas la claridad con que el dominio de la realidad interactúa con
el dominio numérico, y su poder para conceptuar la proporcionalidad (en un caso complejo en
relación a las unidades, incluyendo el caso en que la magnitud cociente no tiene unidades, como
es el caso de la escala 1:200, 1:300, etc.)
El problema 23, como ya hemos analizado, plantea una tarea mucho más compleja, dado que no
es posible realizarlo mediante ninguno de los procedimientos puesto en juego hasta el momento.
El conjunto de problemas utiliza distintos tipos de números: naturales y fraccionarios, éstos
últimos en notación decimal y en notación fraccionaria.
Se utilizan distintas formas de representación: por tablas, verbal y gráfica. El alumno se verá en
la necesidad de traducir los problemas de un lenguaje a otro para interpretarlos y resolverlos.
Los procedimientos involucrados naturalmente son de distinto tipo. A esto se agrega que para
responder deberá, además de obtener un resultado numérico, utilizar críticamente dicho
resultado.
Nos interesa señalar algunos aspectos que deberán someterse a la discusión de todo el grupo de
alumnos a propósito de esta secuencia:
- para determinada elección de unidades, mayor escala (mayor constante) significa un plano
más grande;
- cuando las unidades elegidas para las longitudes en la realidad y en el plano son las
mismas, no es necesario especificarlas y el coeficiente de proporcionalidad no depende de
la unidad elegida: 1:200 significa tanto 1 m para representar 20 m o 1 cm para representar
200 cm. Es decir 1:200 significa 1 unidad (cualquiera sea) para representar 200 de esas
mismas unidades;
- para representar un determinado terreno, la utilización de la escala (escala 1:200) permite
obtener un plano más detallado que si se utilizar al escala 1:300 ya que la fracción 1/200 es
mayor que 1/300. (Esto no resulta evidente para los alumnos que tienden a pensar que
1/300 > 1/200 aplicando una regla (falsa) construida, probablemente, como una
transferencia de lo que ocurre con los números naturales: “como 300 > 200, entonces 1/300
> 1/200”);
- en el caso de escalas, una constante entre 0 y 1, siempre que se utilice la misma unidad para
la realidad y para el mapa, corresponde a una reducción, en cambio una constante mayor
que 1 corresponde a una ampliación (problema 7).
19
Observemos que la explicitación de los aspectos señalados anteriormente a través de una
discusión con los alumnos, posibilita plantear una interacción entre la situación real que da lugar
a la relación de proporcionalidad (en este caso el problema de la escala) y su representación en
el esquema numérico. Pensamos que el estudio en profundidad del funcionamiento de la
proporcionalidad en un contexto determinado, esto es analizar el significado de la constante en
esta aplicación particular, tener en cuenta las variaciones que se producen al cambiar las
unidades, dar sentido al hecho de que la constante sea un número mayor o menor que 1,
etcétera, amplia notablemente las posibilidades de conceptualización. Creemos que cuanto más
rico sea el conjunto de problemas con los que el chico tenga la oportunidad de enfrentarse,
cuantas más relaciones logre establecer, mejores serán las condiciones en las que se encuentre
para poder asimilar situaciones nuevas a su experiencia previa del concepto.
20
Anexo
Una propuesta de problemas para la construcción del campo conceptual multiplicativo de la
escuela primaria.
1- Paola colecciona figuritas. Cada paquete trae 5 figuritas. ¿Cuántas figuritas podrá pegar en
su álbum si compra 8 paquetes?
2- La siguiente tabla muestra la relación entre algunas cantidades de paquetes de figuritas y la
cantidad total de figuritas que se obtienen. Completar la tabla sabiendo que todos los paquetes
traen la misma cantidad de figuritas.
Cantidad de paquetes
Cantidad total de figuritas
4
20
5
8
80
12
60
10
1
160
200
3- Don Francisco y Don Tomás venden las figuritas que colecciona Paola. En el quiosco de
Don Francisco, el precio de 5 paquetes es de $ 3,5. Al precio de Don Tomás, en cambio, el
importe de 8 paquetes es de $ 6. ¿Qué quiosco elegirá Paola? ¿Por qué?
4- ¿Cuánto cuestan 10 paquetes en el quiosco de Don Tomás?
5- Si un chico le compró las figuritas a Don Tomás y gastó $ 27, ¿cuántos paquetes compró?
6- Los chicos del grado de Aníbal van a comprar chocolate para repartir entre ellos, calculando
media tableta por chico. Completar la siguiente tabla.
Cantidad de chicos presentes
18
21
22
23
Cantidad de chocolate consumido
(medido en tabletas)
9
....
11
11 1/2
En algunos casos quedará media tableta sin repartir, ¿cómo es en ese caso el número de chicos?
7- Laura, Aníbal y Julieta se pusieron de acuerdo: al terminar la fiesta dividirán el resto de la
torta en tres partes iguales, una para cada chico. Completar la siguiente tabla que relaciona la
fracción que recibirá cada chico con algunos posibles restos de torta.
Fracción de torta restante
½
Fracción para cada chico
.....
1/3
.....
¼
......
.....
¼
8- En un bote caben 4 personas.¿Cuántos botes se necesitan como mínimo para transportar 25
personas?
9- Con relación al problema anterior: ¿cuántos botes se necesitan si se quiere que en cada bote
vaya la misma cantidad de personas?
10- En un bote caben 4 personas. ¿Cuántos botes se necesitan como mínimo para transportar 24
personas? ¿Y para transportar 28? ¿Cuántas personas se transportan en 8 botes, si todos los
botes se utilizan al máximo de su capacidad?
21
11- Completar la siguiente tabla:
Edad de Aníbal
11
12
23
Edad de Laura
14
12- Uno de estos cuadros corresponde a cantidades que no son directamente proporcionales.
¿Cuál es? ¿Por qué?
2
4
6
4
8
12
2
4
6
4
8
9
13- Para el juego de carreras de autos se dispone de un mazo de tarjetas. Cada tarjeta indica una
velocidad. Comienza el chico que obtiene la tarjeta con mayor velocidad. La tarjeta de Ariel
indica 120 kilómetros por hora, la de Juan Pablo 2 kilómetros por minuto, la de Ignacio 2000
metros por minuto y la de Aníbal 120000 metros por hora. ¿Quién empieza? ¿Por qué?
14- Proponer distintas maneras de controlar el velocímetro de un auto en el que uno circula por
una ruta a velocidad constante.
15- Laura estuvo haciendo un plano para su departamento: un ambiente, cocina baño y un hall de
entrada. Completar la siguiente tabla, sabiendo que con 1 cm, va a representar 1 m (o sea con una
escala 1 cm/m):
Habitación
Baño
Cocina
Hall
Medida real
(en metros)
Medida sobre el plano
(en cm)
Largo
4
.........
Ancho
3,50
.........
Lado
1,50
.........
Largo
3
.........
Ancho
2,50
.........
Lado
1
.........
16- Después probó con otras escalas: ¿Con cuál resultará un plano más grande: con la de 1 cm/m, la
de 1/2 cm/m, o la de 3 cm/m? ¿Por qué?
17- Al fin se decidió por otra escala. El lado del baño quedó, sobre el plano, de 3cm. ¿Qué escala
utilizó esta vez? ¿Por qué?
18- Entusiasmada, agregó un balcón terraza a su último plano. Le quedó así:
¿Qué medidas sueña para su balcón?
22
19- Por último, ya experta en escalas, consideró el siguiente dibujo:
Para ayudarte a entender el tema de escalas, Laura te pide ahora que realices una ampliación y una
reducción del mismo, y que completes luego la siguiente tabla:
Largo
Ancho
Dibujo original (en cm)
Dibujo ampliado (en cm)
Dibujo reducido (en cm)
¿Qué escala utilizaste para la ampliación? ¿Y para la reducción? ¿Qué relación guardan esos
números entre sí? ¿Podrías realizar alguna conjetura?
20- Consultando planos de arquitectos, observó que venían sin unidades: 1: 100; 1: 200; 1: 300….
Se preguntó qué querrían decir, y por qué venían sin unidades. ¿Cómo se le podría explicar?
21- Completar la siguiente tabla, que expresa la relación entre la cantidad de kilómetros y la cantidad
de centímetros contenidos en determinadas longitudes.
Cantidad de kilómetros
1
2
0,02
…….
Cantidad de centímetros
……..
……..
……..
1
22- Reducir a metros: 3 km 2 dam 4 m
3/10 cm
23- Laura tomó un mapa y sacó una fotocopia reducida del mismo. Aquí está:
El mapa original
estaba perfecto,
pero la fotocopia
contiene un
error. ¿Cuál es?
23