scribd.vdownloaders.com analisis-matricial-portico-inclinado

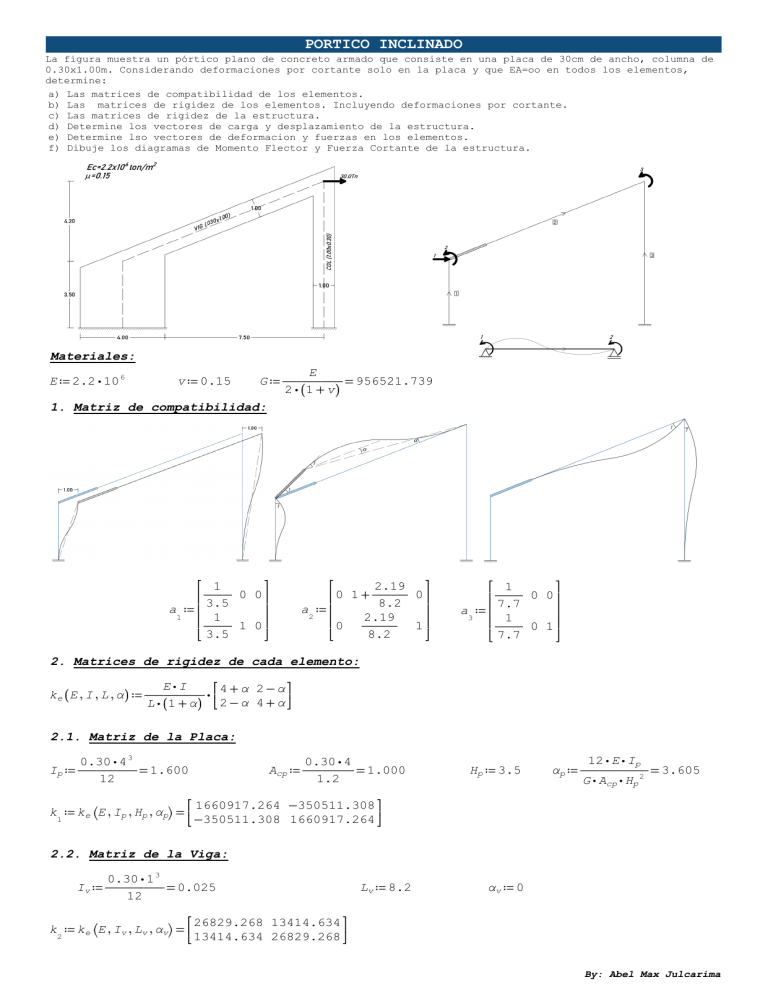
PORTICO INCLINADO
La figura muestra un pórtico plano de concreto armado que consiste en una placa de 30cm de ancho, columna de
0.30x1.00m. Considerando deformaciones por cortante solo en la placa y que EA=oo en todos los elementos,
determine:
a) Las matrices de compatibilidad de los elementos.
b) Las matrices de rigidez de los elementos. Incluyendo deformaciones por cortante.
c) Las matrices de rigidez de la estructura.
d) Determine los vectores de carga y desplazamiento de la estructura.
e) Determine lso vectores de deformacion y fuerzas en los elementos.
f) Dibuje los diagramas de Momento Flector y Fuerza Cortante de la estructura.
Materiales:
E
G ≔ ――――
= 956521.739
2 ⋅ (1 + v)
1. Matriz de compatibilidad:
E ≔ 2.2 ⋅ 10 6
v ≔ 0.15
⎡ 1
⎤
0 0⎥
⎢ ――
3.5
a ≔⎢
⎥
1
1
⎢ ――
1 0⎥
⎢⎣ 3.5
⎥⎦
⎡
⎤
2.19
0⎥
⎢ 0 1 + ――
8.2
a ≔⎢
⎥
2
2.19
⎢ 0 ―― 1 ⎥
⎢⎣
⎥⎦
8.2
⎡ 1
⎤
0 0⎥
⎢ ――
7.7
a ≔⎢
⎥
3
1
⎢ ――
0 1⎥
⎢⎣ 7.7
⎥⎦
2. Matrices de rigidez de cada elemento:
E⋅I
⎡4+α 2-α⎤
⋅
ke (E , I , L , α) ≔ ――――
L ⋅ (1 + α) ⎢⎣ 2 - α 4 + α ⎥⎦
2.1. Matriz de la Placa:
0.30 ⋅ 4 3
Ip ≔ ――――
= 1.600
12
0.30 ⋅ 4
Acp ≔ ―――= 1.000
1.2
Hp ≔ 3.5
12 ⋅ E ⋅ Ip
αp ≔ ――――
= 3.605
G ⋅ Acp ⋅ Hp 2
⎡ 1660917.264 -350511.308 ⎤
k ≔ ke ⎛⎝E , Ip , Hp , αp⎞⎠ = ⎢
1
⎣ -350511.308 1660917.264 ⎥⎦
2.2. Matriz de la Viga:
0.30 ⋅ 1 3
Iv ≔ ――――
= 0.025
12
Lv ≔ 8.2
αv ≔ 0
⎡ 26829.268 13414.634 ⎤
k ≔ ke ⎛⎝E , Iv , Lv , αv⎞⎠ = ⎢
2
⎣ 13414.634 26829.268 ⎥⎦
By: Abel Max Julcarima
2.3. Matriz de la Columna:
0.30 ⋅ 1 3
Ic ≔ ――――
= 0.025
12
Hc ≔ 7.70
αc ≔ 0
⎡ 28571.429 14285.714 ⎤
k ≔ ke ⎛⎝E , Ic , Hc , αc⎞⎠ = ⎢
3
⎣ 14285.714 28571.429 ⎥⎦
3. Matriz de rigidez de la estructura:
K≔ ∑a
i
T
i
i ≔ 1,2‥3
⎡ 215389.508 374401.702 5565.863 ⎤
⋅ k ⋅ a = ⎢ 374401.702 1714983.706 24162.701 ⎥
i
i
⎢⎣ 5565.863
24162.701 55400.697 ⎥⎦
4. Matriz de rigidez lateral:
⎡1⎤
Ql ≔ ⎢ 0 ⎥
⎢⎣ 0 ⎥⎦
Dl ≔ K
-1
⎡ 7.482 ⋅ 10 -6 ⎤
⎢
⎥
Dl = -1.633 ⋅ 10 -6
⎢
⎥
-8
⎣ -3.952 ⋅ 10 ⎦
⋅ Ql
Fl ≔ Dl
1,1
= 7.482 ⋅ 10 -6
Kl ≔ Fl -1 = 1.337 ⋅ 10 5
5. Desplazamientos y giros en los GDL globales:
Principio de trabajo virtual (Teorema de Betti)
⎡ 30 ⎤
⎢
Q≔ 0 ⎥
⎢⎣ 0 ⎥⎦
⎡ 2.245 ⋅ 10 -4 ⎤
⎢
D = -4.899 ⋅ 10 -5 ⎥
⎢
⎥
-6
⎣ -1.186 ⋅ 10 ⎦
D ≔ K -1 ⋅ Q
6. Giros en los GDL locales:
⎡ 6.413 ⋅ 10 -5 ⎤
d ≔a ⋅D=⎢
-5 ⎥
1
1
⎣ 1.515 ⋅ 10 ⎦
⎡ -6.207 ⋅ 10 -5 ⎤
d ≔a ⋅D=⎢
-5 ⎥
2
2
⎣ -1.427 ⋅ 10 ⎦
⎡ 2.915 ⋅ 10 -5 ⎤
d ≔a ⋅D=⎢
-5 ⎥
3
3
⎣ 2.797 ⋅ 10 ⎦
7. Fuerzas en los GDL locales:
q ≔k ⋅d
1
1
1
⎡ 101.210 ⎤
q =⎢
1
⎣ 2.677 ⎥⎦
q ≔k ⋅d
2
2
q ≔k ⋅d
2
3
⎡ -1.857 ⎤
q =⎢
2
⎣ -1.215 ⎥⎦
3
3
⎡ 1.232 ⎤
q =⎢
3
⎣ 1.215 ⎥⎦
8. Diagrama de momento flector (DMF):
By: Abel Max Julcarima
9. Diagrama de fuerza cortante (DFC):
By: Abel Max Julcarima