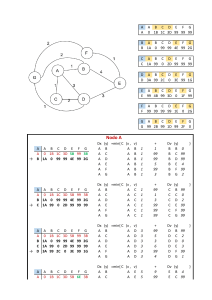
CLASE 5/05 Con base en este análisis de sensibilidad, se concluye que los resultados para la alternativa de decisión del complejo grande (d3) podrían variar de manera considerable, y d3 seguiría siendo la alternativa de decisión recomendada. Por esta razón se concluye que la solución óptima para el problema de decisión de PDC no es particularmente sensible a los resultados de la alternativa de decisión del complejo grande. Análisis de decisiones con información muestral Con mayor frecuencia, la información adicional se obtiene por medio de experimentos diseñados para proporcionar información muestral acerca de los estados de la naturaleza. El muestreo de materias primas, las pruebas de productos y la investigación de mercados son ejemplos de experimentos. Estas probabilidades revisadas se llaman probabilidades posteriores. Retomemos el problema de PDC y suponga que la gerencia considera una investigación de mercados de seis meses para aprender más sobre la posible aceptación del proyecto de condominios de PDC en el mercado. La gerencia anticipa que dicha investigación proporcionará uno de los dos resultados siguientes: 1. Informe favorable: Un número significativo de las personas contactadas expresa interés en la compra de un departamento en los condominios de PDC. 2. Informe desfavorable: Muy pocas de las personas contactadas expresan interés en la compra de un departamento en los condominios de PDC Diagrama de influencia Al introducir la posibilidad de realizar una investigación de mercados, el problema de PDC se vuelve más complejo. El diagrama de influencia para el problema de PDC expandido se muestra en la figura: Observe que los dos nodos de decisión corresponden a la investigación y a las decisiones del tamaño del complejo. Los dos nodos fortuitos corresponden a los resultados de la investigación y a la demanda de los condominios El nodo de consecuencia son las utilidades. A partir de los arcos del diagrama de influencia, vemos que la demanda influye tanto en los resultados de la investigación como en las utilidades. En este sentido, la demanda existente para los condominios influirá en los resultados de la investigación y, desde luego, también influirá en las utilidades de PDC. El arco que va del nodo de decisión de la investigación al nodo de decisión del tamaño del complejo indica que la decisión de la investigación precede a la decisión del tamaño del complejo. Árbol de decisión El árbol de decisión para el problema de PDC con la información muestral exhibe la secuencia lógica de las decisiones y los eventos fortuitos Primero, la gerencia de PDC debe decidir si la investigación de mercados se realiza o no. Si se hace, la gerencia debe estar preparada para tomar una decisión respecto al tamaño del proyecto de condominios si el informe de la investigación de mercados es favorable y, posiblemente, una decisión diferente sobre si el informe es desfavorable. El análisis del árbol de decisión y la opción de una estrategia óptima requieren que se conozcan las probabilidades de las ramas que corresponden a todos los nodos fortuitos. PDC ha desarrollado las siguientes probabilidades de ramas: Si se realiza la investigación de mercados: P (Informe favorable) = 0.77 P (Informe desfavorable) = 0.23 Si el informe de investigación de mercados es favorable: P (Demanda fuerte dado un informe favorable) = 0.94 P (Demanda débil dado un informe favorable) = 0.06 Si el informe de investigación de mercados es desfavorable: P (Demanda fuerte dado un informe favorable) = 0.35 P (Demanda débil dado un informe favorable) = 0.65 Si el informe de investigación de mercados no se realiza, las probabilidades previas son aplicables. P (Demanda fuerte) = 0.80 P (Demanda débil) = 0.20 VE (Nodo 6) = 0.94(8) + 0.06(7) = 7.94 VE (Nodo 7) = 0.94(14) + 0.06(5) = 13.46 VE (Nodo 8) = 0.94(20) + 0.06(9) = 18.26 VE (Nodo 9) = 0.35(8) + 0.65(7) = 7.35 VE (Nodo 10) = 0.35(14) + 0.65(5) = 8.15 VE (Nodo 11) = 0.35(20) + 0.65(9) = 1.15 VE (Nodo 12) = 0.80(8) + 0.20(7) = 7.80 VE (Nodo 13) = 0.80(14) + 0.20(5) = 12.20 VE (Nodo 14) = 0.80(20) + 0.20(9) = 14.20 VE (Nodo 3) = mayor valor entre 6 ,7 y 8 = 18.26 d3 favorable VE (Nodo 4) = mayor valor entre 9 ,10 y 11 = 8.15 d2 desfavorable VE (Nodo 5) = mayor valor entre 12 ,13 y 15 = 14.20 d3 VE (Nodo 2) = 0.77(18.26) + 0.23(8.15) = 15.93 VE (Nodo 1) = mayor valor entre 2 y 5 = 15.93 Mejor decisión realizar la investigación de mercados Estrategia de decisión • Una estrategia de decisión es una secuencia de decisiones y resultados fortuitos donde las decisiones elegidas dependen de los resultados aún por determinar de los eventos fortuitos. El método utilizado para determinar la estrategia de decisión óptima se basa en avanzar en sentido inverso por el árbol de decisión siguiendo estos pasos: 1. En los nodos fortuitos, calcule el valor esperado mediante la multiplicación del resultado al final de cada rama por las probabilidades de rama correspondientes. 2. En los nodos de decisión, seleccione la rama de decisión que conduzca al mejor valor esperado, el cual se vuelve el valor esperado en el nodo de decisión. A continuación, pase los nodos de decisión 3, 4 y 5. Para cada uno de estos nodos seleccionamos la rama de la alternativa de decisión que conduce al mejor valor esperado. Debemos seleccionar la rama de la alternativa de decisión que conduce al mejor valor esperado. Por ejemplo: En el nodo 3 tenemos: La opción de la rama del complejo pequeño Con VE(Nodo 6) 7.94, la rama del complejo mediano con VE(Nodo 7) 13.46. La rama del complejo grande con VE(Nodo 8) = 18.26. Por tanto, seleccionamos la rama de la alternativa de decisión del complejo grande y el valor esperado en el nodo 3 se vuelve VE(Nodo 3) 18.26. Para el nodo 4 se selecciona el mejor valor esperado a partir de los nodos 9, 10 y 11. La mejor alternativa de decisión es la rama del complejo mediano que proporciona VE(Nodo 4) = 8.15 Para el nodo 5 se selecciona el mejor valor esperado a partir de los nodos 12, 13 y 14. La mejor alternativa de decisión es la rama del complejo grande que proporciona VE(Nodo 5) = 14.20 Lo interesante es la diferencia entre estos dos valores ya que será la ganancia de la empresa que haga la investigación Por último, se puede tomar la decisión en el nodo de decisión 1 al seleccionar los mejores valores esperados de los nodos 2 y 5. Esta acción conduce a la alternativa de decisión de realizar la investigación de mercados, lo cual proporciona un valor esperado general de 15.93. SOLUCION: • La decisión óptima para PDC es realizar la investigación de mercados y luego implementar la siguiente estrategia de decisión: • Si la investigación de mercados es favorable, construir el complejo de condominios grande. • Si la investigación de mercados es desfavorable, construir el complejo de condominios mediano. Perfil de riesgo La figura presenta un árbol de decisión reducido que muestra sólo la secuencia de las alternativas de decisión y los eventos fortuitos para la estrategia de decisión óptima de PDC. Recuerde que un perfil de riesgo muestra los resultados posibles con sus probabilidades asociadas. Por tanto, para construir un perfil de riesgo para la estrategia de decisión óptima, necesitamos calcular la probabilidad para cada uno de los cuatro resultados. Observe cada uno de los resultados de una secuencia de ramas que salen del nodo 1 al resultado. Esto es teorema de Bayes, ya que dado un suceso cual es la probabilidad de otro suceso Redujo la probabilidad de la pérdida de $9 millones de 0.20 a 0.05. Es muy probable que la gerencia de PDC viera ese cambio como una reducción significativa en el riesgo asociado con el proyecto de condominios. Valor esperado de la información muestral • En el problema de PDC, la investigación de mercados es la información muestral utilizada para determinar la estrategia de decisión óptima. El valor esperado asociado con la investigación de mercados es $15.93 En la sección mostramos que el mejor valor esperado si no se realiza la investigación de mercados es $14.20 • En otras palabras, la información de la investigación de mercados es 54.1% tan eficiente como la información perfecta. • Las estimaciones de eficiencia bajas para la información muestral podrían llevar al tomador de decisiones a buscar otros tipos de información. Sin embargo, las calificaciones de eficiencia altas indican que la información muestral es casi tan buena como la información perfecta y que las fuentes adicionales de información no producirían resultados significativamente mejores. Menos de 30% es ineficiente y más de 70% muy buena, en nuestro caso es decente el resultado. Cálculo de probabilidades de las ramas o alternativas • En la sección anterior los nodos fortuitos de las probabilidades de las ramas para el árbol de decisión de PDC se especificaron en la descripción del problema. No se requirieron cálculos para determinar estas probabilidades. En esta sección se muestra cómo el teorema de Bayes puede utilizarse para calcular las probabilidades de las ramas para los árboles de decisión El árbol de decisión de PDC se muestra de nuevo en la figura Sea: F = informe de investigación del mercado favorable U = informe de investigación del mercado desfavorable S1 = demanda fuerte (estado de la naturaleza 1) S2 = demanda débil (estado de la naturaleza 2) • En el nodo fortuito 2 necesitamos conocer las probabilidades de las ramas P(F) y P(U). En los nodos de probabilidad 6, 7 y 8 necesitamos conocer las probabilidades de: • De la rama P(s1 | F), la probabilidad del estado de la naturaleza 1 dado un informe de investigación de mercados favorable De la rama P(s2 | F), la probabilidad del estado de la naturaleza 2 dado un informe de investigación de mercados favorable. • P(s1 | F) y P(s2 | F) se conocen como probabilidades posteriores debido a que son probabilidades condicionales basadas en el resultado de la información muestral. • En los nodos de probabilidad 9, 10 y 11 necesitamos conocer las probabilidades de las ramas P(s1 | U) y P(s2 | U); En los nodos fortuitos 12, 13 y 14, necesitamos las probabilidades para los estados de la naturaleza, P(s1) y P(s2), si la investigación de mercados no se realiza. Al hacer los cálculos de probabilidad necesitamos conocer la evaluación de PDC de las probabilidades para los dos estados de la naturaleza, P(s1) y P(s2) que son las probabilidades previas expuestas antes. Debemos conocer la probabilidad condicional de los resultados de la investigación de mercados (la información muestral) dado cada estado de la naturaleza. Observe que las evaluaciones de probabilidad anteriores proporcionan un grado razonable de confianza en la investigación de mercados. Si el verdadero estado de la naturaleza es s1, la probabilidad de un informe de investigación de mercados favorable es 0.90, y la probabilidad de un informe desfavorable es 0.10. Si el estado de la naturaleza verdadero es s2, la probabilidad de un informe de investigación de mercados favorable es 0.25, y de uno desfavorable es 0.75 • La razón por la cual se asigna 0.25 a la probabilidad para un informe potencialmente engañoso de investigación de mercados favorable con un estado de la naturaleza s2, es que cuando algunos compradores potenciales escuchan por primera vez acerca del nuevo proyecto de condominios, su entusiasmo puede llevarlos a exagerar su interés real en él. La respuesta favorable inicial de un posible comprador puede cambiar rápidamente a "no gracias" cuando se enfrente más tarde a la realidad de tener que firmar un contrato de compra y hacer un pago inicial • A continuación se presenta un enfoque tabular como un método conveniente para realizar los cálculos de probabilidad. Los cálculos para el problema de PDC basados en un informe de investigación de mercados favorable (F) se resumen en la tabla. Los pasos utilizados para desarrollar esta tabla son los siguientes: •Paso 1. En la columna 1 introduzca los estados de la naturaleza. En la columna 2 escriba las probabilidades previas para los estados de la naturaleza. En la columna 3 indique las probabilidades condicionales de un informe de investigación de mercados favorable (F) dado cada estado de la naturaleza. Paso 2. En la columna 4 calcule las probabilidades conjuntas al multiplicar los valores de probabilidad previa de la columna 2 por los valores de probabilidad condicional correspondientes de la columna 3. Observe que un informe de investigación de mercados favorable provocará una probabilidad revisada o posterior de 0.94 de que la demanda de mercado de los condominios será fuerte, 51. El procedimiento de cálculo de la probabilidad tabular debe repetirse para cada resultado de información muestral posible. • Por tanto, la tabla muestra los cálculos de las probabilidades de las ramas del problema de PDC basados en un informe de investigación de mercados desfavorable. Glosario Evento fortuito Evento futuro incierto que afecta la consecuencia o resultado, asociado con una decisión. Nodos de decisión Nodos que indican puntos donde se toma una decisión. Nodos fortuitos Nodos que indican puntos dónde ocurrirá un evento incierto. Nodos de consecuencia Nodos de un diagrama de influencia que indican puntos donde ocurrirá un resultado. Árbol de decisión Representación gráfica del problema de decisión que muestra la naturaleza secuencial del proceso de toma de decisiones. Perfil de riesgo Distribución de probabilidad de los resultados posibles asociados con una alternativa de decisión o estrategia de decisión Un pronostico es una estimación que es probable que ocurra en el futuro, basado en análisis, juicios y experiencias y preferentemente en alguna clase de modelo matemático que refleje el comportamiento de datos. Datos cuantitativos 1. Deben existir datos numéricos 2. Debe cumplirse la hipótesis de continuidad Selección del método depende del comportamiento de los datos, el método debe ser preciso y entendible, y el método debe proveer un beneficio. Elaboración de pronósticos Un aspecto esencial de la administración de cualquier organización es la planeación del futuro. En efecto, el éxito a largo plazo de una organización depende de cuán bien la gerencia anticipa el futuro y elabora las estrategias apropiadas El buen juicio, la intuición y tener conciencia del estado de la economía pueden dar a un gerente una idea aproximada o "intuición" de lo que es probable que suceda en el futuro. Sin embargo, con frecuencia es difícil convertir esta intuición en un número que pueda usarse Los modelos a verse a continuación son numéricos • Como el volumen de ventas del siguiente trimestre o el costo de la materia prima por unidad para el año próximo EJEMPLO Suponga que le hemos pedido que proporcione pronósticos trimestrales del volumen de ventas para un producto en particular durante el año próximo Dichos pronósticos afectarán los programas de producción, los planes de compra de materias primas, las políticas de inventarios y las cuotas de ventas. En consecuencia, los malos pronósticos pueden dar como resultado un incremento en los costos de la empresa. ¿Cómo debemos proceder para proporcionar los pronósticos trimestrales del volumen de ventas? Desde luego, deberíamos revisar los datos de las ventas reales del producto en periodos anteriores. Con estos datos históricos podemos identificar el nivel general de ventas y cualquier tendencia, como un incremento o disminución en el volumen de ventas con respecto al tiempo. Una revisión más a fondo de los datos podría revelar un patrón estacional, como las ventas máximas que ocurren en el tercer trimestre de cada año y el volumen de ventas que alcanza su nivel más bajo durante este primer trimestre Al revisar los datos históricos, con frecuencia podemos comprender mejor el patrón de las ventas pasadas, lo que conduce a mejores predicciones de las ventas futuras del producto Los datos históricos de ventas forman una serie de tiempo • Una serie de tiempo es un conjunto de observaciones de una variable medida en puntos sucesivos en el tiempo o a lo largo de periodos sucesivos • Los métodos de elaboración de pronósticos se clasifican como cuantitativos o cualitativos. Los métodos cuantitativos se utilizan cuando: 1) se dispone de información pasada sobre la variable que se pronosticará. 2) la información puede cuantificarse. 3) es razonable suponer que el patrón del pasado seguirá ocurriendo en el futuro. Si los datos históricos se restringen a valores pasados de la variable que tratamos de pronosticar, el procedimiento de elaboración de pronósticos se llama método de serie de tiempo El objetivo de los métodos de serie de tiempo es descubrir un patrón en los datos históricos y luego extrapolarlo hacia el futuro; el pronóstico se basa sólo en valores pasados de la variable que tratamos de pronosticar o en errores pasados. - En este capítulo se explican tres métodos de series de tiempo: Suavización (promedios móviles, promedios móviles ponderados y suavización exponencial), Proyección de tendencias y Proyección de tendencias ajustada por influencia estacional • Los métodos de elaboración de pronósticos causal se basan en el supuesto de que la variable que tratamos de pronosticar exhibe una relación de causa y efecto con una o más variables En este capítulo se estudia el uso del análisis de regresión lineal como un método de elaboración de pronósticos causal EJEMPLO • los gastos de publicidad influyen en el volumen de ventas de muchos productos, de manera que el análisis de regresión puede utilizarse para desarrollar una ecuación que muestre cómo se relacionan estas dos variables Luego, una vez establecido el presupuesto de publicidad para el periodo siguiente, podríamos sustituir este valor en la ecuación con el fin de hacer una predicción o pronóstico del volumen de ventas para ese periodo. Observe que si se utilizó un método de series de tiempo para elaborar el pronóstico, ni siquiera se han considerado los gastos de publicidad; es decir, un método de serie de tiempo habría basado el pronóstico sólo en las ventas pasadas. ANALISIS DE SERIES DE TIEMPO – APLICACIONES LINEAL: y = a + bx PARABOLICA O CUADRATICO: y = a + bx + cx2 Componentes de una serie de tiempo • El patrón o comportamiento de los datos en una serie de tiempo tiene varios componentes. El supuesto usual es que cuatro componentes separados: tendencia, cíclico, estacional e irregular, se combinen para proporcionar valores específicos de la serie de tiempo. componente de tendencia • En el análisis de las series de tiempo, las mediciones pueden tomarse cada hora, día, semana, mes o año, o en cualquier otro intervalo regular. • Aunque los datos de series de tiempo por lo general exhiben fluctuaciones aleatorias, las series de tiempo pueden seguir mostrando cambios o movimientos graduales hacia valores relativamente mayores o menores en un periodo prolongado. • El cambio gradual de la serie de tiempo se conoce como tendencia en la serie de tiempo. •Este cambio o tendencia por lo general es el resultado de factores a largo plazo, como cambios en la población, características demográficas de la población, tecnología y preferencias de consumo. EJEMPLO • un fabricante de equipo fotográfico puede observar una variabilidad significativa cada mes en el número de cámaras vendidas. Sin embargo, en la revisión de ventas de los 10 o 15 años anteriores, este fabricante puede notar un incremento gradual en el volumen de ventas anual. Suponga que en 1996 el volumen de ventas por mes fue aproximadamente de 1,700 cámaras, en 2001 de 2,300 y en 2006 de 2,500. Aunque los volúmenes de ventas mensuales pueden variar de forma considerable, este crecimiento gradual en las ventas indica una tendencia ascendente en la serie de tiempo. La figura 6. muestra una línea recta que puede ser una buena aproximación de la tendencia en la venta de cámaras. https://www.youtube.com/watch?v=IDgu6PuPxYM