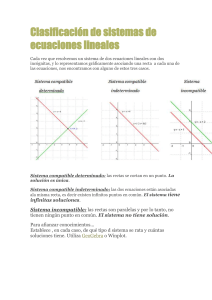
COORDINACIÓN ACADÉMICA Y DE INVESTIGACIÓN División de Ciencias Exactas, Ingeniería y Tecnología Lic. en Enseñanza de las matemáticas 3er. Semestre Módulo # 5 Algebra Lineal. NOMBRE DEL ESTUDIANTE: FERNANDO LOPEZ CASTAÑON. GRUPO: EM-EMAL-2302-B1-002 DOCENTE EN LÍNEA: MARISOL MENDOZA ROSALES. Módulo # Actividad 1. Sistema de Ecuaciones (Método Gráfico). Introducción. Como sabemos los sistemas de ecuaciones es una igualdad entre dos expresiones que contienen dos o más variables (Alex, 2018). Existen diversos métodos de solución, dentro de los cuales veremos durante el desarrollo de la actividad el método gráfico, el método de reducción y la regla de Cramer. Cabe mencionar que haremos uso de un poco de algebra básica al realizar despejes, pero sobre todo de geometría mediante el desarrollo de la ecuación en un plano cartesiano, en busca de los puntos de intersección (si es que llegasen a existir) que serían las soluciones, por lo cual haremos uso del programa GeoGebra, para facilitar su interpretación. Desarrollaremos algunos sistemas de ecuaciones interpretando datos de algunos problemas que son planteados, teniendo algo de criterio e intuición matemática. Así como también comprobaremos mediante dos métodos todos los ejercicios propuestos. UnADM | DCEIT | EM | 2 Módulo # Desarrollo. 1. Resuelve los siguientes ejercicios de sistemas de ecuaciones, usando de forma obligatoria el método de solución gráfica (utiliza algún software) y un método de solución algebraica. R= Primeramente y como parte del método grafico iniciaremos asignando valor de “0” a X y Y, a ambas ecuaciones, esto con el fin de poder encontrar el punto de intersección. (Julio, 2012) 𝑥 + 2𝑦 = 4 X Y 0 2 4 0 UnADM | DCEIT | EM | 3x – y = 5 X Y 0 -5 5/3 0 3 Módulo # Trazamos los datos usando GeoGebra y buscamos el punto de intersección para ambas rectas, dicha intersección será nuestra solución, que en este caso es: X=2 Y=1 Comprobamos mediante el método de reducción: Multiplicamos por los términos que se deseen eliminar cambiando el signo de uno de ellos y procedemos a realizar las operaciones (Alex, 2018): [𝑥 + 2𝑦 = 4 ] (3) ║ 3x + 6y =12 ║ 7y = 7: y = 1 [3𝑥 − 𝑦 = 5 ] (−1) ║-3x + y = -5 Finalmente sustituimos en la ecuación 1 el valor encontrado: X + 2(1) = 4; x + 2 = 4: x = 2 Con esto comprobamos que el resultado obtenido es el mismo. ______________________________________________________________________________ UnADM | DCEIT | EM | 4 Módulo # R= Primeramente y como parte del método grafico iniciaremos asignando valor de “0” a X y Y, a ambas ecuaciones, esto con el fin de poder encontrar el punto de intersección. (Julio, 2012) 𝑥 − 2𝑦 = 6 3x – 6y = 18 X Y X Y 0 -3 0 -3 6 0 6 0 Como vemos, tenemos el caso de dos rectas superpuestas, lo que nos da una cantidad de soluciones infinitas (Julio, 2012) Podemos comprobar esto mediante el grafico con GeoGebra: Comprobamos mediante el método de eliminación: UnADM | DCEIT | EM | 5 Módulo # Multiplicamos por los términos que se deseen eliminar cambiando el signo de uno de ellos y procedemos a realizar las operaciones (Alex, 2018): [𝑥 − 2𝑦 = 6] (-3) ║ -3x + 6y = -18 [3x – 6y = 18] (1) ║ 3x – 6y = 18 Podemos comprobar que el resultado coincide, pero tenemos dos rectas superpuestas (multiples soluciones). ______________________________________________________________________________ R= Primeramente y como parte del método grafico iniciaremos asignado valor de “0” a X, Y y Z, a todas las ecuaciones, esto con el fin de poder encontrar el punto de intersección. (Calderón, 2020). 2𝑥 − 𝑦 + 5𝑧 = 16 𝑥 − 6𝑦 + 2𝑧 = −9 3𝑥 + 4𝑦 − 𝑧 = 32 X Y Z X Y Z X Y Z 8 0 0 -9 0 0 32/3 0 0 0 -16 0 0 3/2 0 0 8 0 0 0 16/5 0 0 -9/2 0 0 -32 Trazamos los datos usando GeoGebra y buscamos el punto de intersección para ambas rectas, dicha intersección será nuestra solución, que en este caso es: UnADM | DCEIT | EM | 6 Módulo # Ahora comprobamos mediante el método de reducción: Para ello eliminamos primeramente 1 con 2, y 1 con 3, con el fin de encontrar dos nuevas ecuaciones (Darwin, 2021): 1) [2𝑥 − 𝑦 + 5𝑧 = 16] (-1) ║ −2𝑥 + 𝑦 − 5𝑧 = −16 ║ -11y – z = -34 Ec. 4 2) [𝑥 − 6𝑦 + 2𝑧 = −9] (2) ║2𝑥 − 12𝑦 + 4𝑧 = −18 UnADM | DCEIT | EM | 7 Módulo # 1) [2𝑥 − 𝑦 + 5𝑧 = 16] (-3) ║ -6x + 3y -15z = -48 ║11y – 17z = 16 Ec. 5 2) [3x + 4y – z = 32] (2) ║ 6x + 8y -2z = 64 Como siguiente paso reducimos las nuevas ecuaciones obtenidas con el fin de encontrar el valor de una de las incógnitas (Darwin, 2021): -11y – z = -34 11y – 17z = 16 Como vemos los primeros términos son iguales en valor y con diferente signo, por lo que podemos realizar directamente una eliminación, obteniendo el siguiente resultado: -18 z = -18: z = 1 Ahora sustituimos el valor encontrado en cualquiera de las ecuaciones que hayamos previamente, para este caso tomaremos la ecuación 5: 11y – 17 (1) = 16; 11y = 33: y = 3 Por último, sustituimos ambos valores en una de las ecuaciones originales, para este caso utilizaremos la ecuación 1: 2x – y + 5z = 16; 2x –(3) + 5(1) = 16; 2x + 2 = 16: x = 7 Con esto demostramos que ambos resultados de los métodos empleados nos dan el mismo resultado. X Y Z 7 3 1 UnADM | DCEIT | EM | 8 Módulo # Resuelve los siguientes problemas, utiliza dos métodos para generar una comprobación. a) Un vendedor de libros de ciencias vendió tres de geometría analítica y 5 de álgebra lineal en $870. Al día siguiente, vendió 2 de geometría analítica y 3 de álgebra lineal en $540, ¿cuál es el precio de cada libro? R= Lo primero es plantear en forma de ecuación los datos proporcionados por el problema, para ello asignaremos una incógnita a cada tipo de libro, siendo Geometría Analítica = x, y Algebra lineal = y. (Superprof. 2020) 3𝑥 + 5𝑦 = 870 2𝑥 + 3𝑦 = 540 Usando el método gráfico, procedemos a asignar los valores de “0” a X y Y, para ambas ecuaciones: 3𝑥 + 5𝑦 = 870 2𝑥 + 3𝑦 = 540 X Y X Y 0 174 0 180 290 0 270 0 Ahora procedemos a graficar con GeoGebra y encontrar el punto de intersección, el cual será nuestro resultado (Julio, 2012) UnADM | DCEIT | EM | 9 Módulo # Ahora comprobaremos nuestros resultados mediante el método de reducción, para demostrar que el resultado es el mismo: [3𝑥 + 5𝑦 = 870] (-2) ║ -6x -10y = -1740 ║-y = -120: y = 120 [2𝑥 + 3𝑦 = 540] (3) ║ 6x + 9y = 1620 Sustituyendo el valor obtenido en una de las ecuaciones originales (para este caso usamos la Ecuación No.2 = 2x + 3(120) = 540; 2x= 180: x = 90. Con esto, comprobamos que nuestros resultados coinciden: X Y 90 120 b) Un mexicano especialista en mezclas de café desea exportar el grano en bolsas que contengan un kilogramo. Debe combinar granos de los estados de Chiapas y Veracruz. El costo por kilogramo de estos tipos de café es $30 y $24 respectivamente. Si la bolsa cuesta $25.50, ¿qué cantidad de cada café lleva dicha mezcla? R= Lo primero es plantear en forma de ecuación los datos proporcionados por el problema, para ello asignaremos una incógnita a cada una de las variables, siendo “x” el café de Chiapas y “y” el café de Veracruz, por otro lado, los costos y la cantidad de ambos tipos de café, pueden ser planteados por otra ecuación. (Superprof. 2020) 𝑥 + 𝑦 = 1 (considerando que 1 es el 100% de la mezcla.) 30𝑥 + 24 𝑦 = 25.50 UnADM | DCEIT | EM | 10 Módulo # Usando el método gráfico, procedemos a asignar los valores de “0” a X y Y, para ambas ecuaciones: 𝑥+𝑦=1 30𝑥 + 24 𝑦 = 25.50 X Y X Y 0 1 0 1.06 1 0 0.85 0 Ahora procedemos a graficar con GeoGebra y encontrar el punto de intersección, el cual será nuestro resultado (Julio, 2012): Ahora comprobaremos nuestros resultados mediante el método de reducción, para demostrar que el resultado es el mismo, los pasos a seguir son siempre los mismos, por lo que procedemos a multiplicar por los 2 primos coeficientes de cualquier incógnita, para este caso será “x”. [𝑥 + 𝑦 = 1] (30) ║ 30x + 30 y = 30 [30𝑥 + 24 𝑦 = 25.50] (-1) ║-30x – 24y = -25.50 UnADM | DCEIT | EM | ║ 6y = 4.5: y = 0.75 11 Módulo # Sustituyendo el valor encontrado en cualquier función y despejando “y”: X + 0.75 = 1; x = 0.25 Como podemos ver, nuestros resultados son iguales. c) Carlos y Gabriel fueron al supermercado a comprar lo necesario para una reunión con amigos del colegio, llevaban un total de $500 para gastar. Carlos gastó dos terceras partes de su dinero, mientras que Gabriel tres quintas partes, regresaron a casa con un total de $180, ¿cuánto llevaba cada uno al ir al supermercado? R= Lo primero es plantear en forma de ecuación los datos proporcionados por el problema, para ello asignaremos una incógnita a cada dato, considerando primeramente el total y posteriormente las partes gastadas, teniendo en consideración que es lo que ellos poseen aún. (Superprof. 2020): 𝑥 + 𝑦 = 500 1 3 𝑥+ 2 5 𝑦 = 180 Consideramos un tercio y 2 quintos por que es lo que les quedo en su poder a forma de residuo de $180 pesos. Primero lo solucionaremos por medio del método de reducción: [𝑥 + 𝑦 = 500] (1/3) 1 [3 𝑥 + 2 5 1 1 ║ 3𝑥 + 3𝑦 = 1 𝑦 = 180] (-1) ║− 3 𝑥 − 2 5 500 1 ║− 15 𝑦 = − 3 𝑦=− 40 3 ∶. y = 200 540 3 Ahora sustituimos en cualquiera de las ecuaciones originales (en este caso la primera): x + (200) = 500: x= 300 Ahora comprobaremos mediante el método Gráfico si nuestros resultados son correctos: UnADM | DCEIT | EM | 12 Módulo # Primeramente y como parte del método grafico iniciaremos asignando valor de “0” a X y Y, a ambas ecuaciones, esto con el fin de poder encontrar el punto de intersección. 𝑥 + 𝑦 = 500 1 𝑥+ 3 2 5 𝑦 = 180 X Y X Y o 500 o 450 500 0 540 0 Ahora procedemos a graficar con GeoGebra y encontrar el punto de intersección, el cual será nuestro resultado (Julio, 2012): Como vemos nuestros resultados son los mismos por ambos métodos. UnADM | DCEIT | EM | 13 Módulo # Responde a las preguntas de reflexión: • ¿Has intentado graficar a mano planos en un sistema de ejes coordenados xyz? R= Si lo he intentado, pero debido a que la proyección de 3 planos es en 3 dimensiones, y el hecho de plasmarlo en un papel, lo limita a 2 dimensiones, por lo que es un poco complicado analizar la figura, sobre todo cuando los puntos se extienden por los diferentes cuadrantes. Cabe mencionar que si están en el mismo cuadrante es un poco mas sencillo de interpretar y también de trazar. Con la ayuda de GeoGebra, la historia es diferente pues tenemos una proyección en una sola figura de todos los cuadrantes, lo que facilita, la interpretación de los resultados. • ¿Qué tan efectivo te parece el método gráfico para resolver un sistema de 3x3? R= Es efectivo, de hecho, tiene un alto grado de efectividad, pero se pude complicar un poco cuando entran en función los decimales, de hecho, es menos laborioso que otros métodos como Cramer o Gauss, pero esto si se cuanta, con la ayuda de un programa de apoyo, como en este caso fue GeoGebra. Aun que definitivamente el realizar los ejercicios usando dos métodos es mucho mejor cuando “no” se cuenta con GeoGebra, pues como dijimos anteriormente, la interpretación de los planos se puede complicar a la hora de plasmarlo en papel, además de que, sin una hoja milimétrica, se vuelve aún más tedioso. • ¿Qué provecho crees que se pueda sacar de este método? R= Por su alto grado de efectividad, puede ser utilizado siempre como un método de comprobación, siempre y cuando (repito) se cuente con un software de grafica. Además de ser la base para cualquier método, siempre y cuando se tenga 2 o 3 incógnitas. Considero que su única desventaja es lo laborioso que puede llegar a ser de forma manual. UnADM | DCEIT | EM | 14 Módulo # Conclusiones. Como vimos a lo largo del desarrollo de esta actividad, el método grafico es la base de la cual se tiene que partir para la interpretación grafica de la solución de un sistema de ecuaciones. Además de ser bastante preciso, es una forma eficaz de comprobar si el sistema tiene solución, tiene múltiples soluciones o bien no tiene solución. (Julio, 2012) Este método se facilita con el apoyo de un software de gráfica, haciendo relativamente fácil y rápido de solucionar y sobre todo de poder entender, mas aun cuando estamos trabajando en tercera dimensión. Cabe mencionar que debido a que el objetivo de la actividad era tener una base sólida del método gráfico, hicimos uso de el en todos los ejercicios, habiendo únicamente un ejercicio el cual era un sistema dependiente con dos rectas superpuestas tenido múltiples soluciones. A lo largo de la actividad utilizamos únicamente los métodos de reducción o eliminación y el método gráfico, encontrándonos con 3 tipos de sistemas de ecuaciones: el dependiente (muchas soluciones), el consistente (única solución) y el inconsistente (solución nula). (Alex, 2018). UnADM | DCEIT | EM | 15 Módulo # Referencias Bibliográficas. IngEDarwin. (2021, junio 29). Método de Reducción - Sistema de Ecuaciones Lineales 3x3, Ejercicio 1 [Vídeo]. YouTube https://www.youtube.com/watch?v=vPCoCeV8JXs MATEMATICAS con Calderón (2020, julio 5). Sistemas 3x3 método gráfico 2 [Vídeo]. YouTube https://www.youtube.com/watch?v=wpXxaWEMG2c Matemáticas profe Alex. (2018, mayo 15). Sistemas de ecuaciones 2x2, Método de Reducción – Eliminación, Ejemplo 2 [Vídeo]. YouTube https://www.youtube.com/watch?v=UMNcW4hjQK8 Julioprofenet. (2012, abril 29). Solución de un Sistema de Ecuaciones de 2x2 por el Método Gráfico [Vídeo]. YouTube https://www.youtube.com/watch?v=eMug3FSoOZk Julioprofenet. (2012, mayo 6). Sistema de 3x3 resuelto por Regla de Cramer [Vídeo]. YouTube https://www.youtube.com/watch?v=lLPcHVAqY80 UnADM | DCEIT | EM | 16