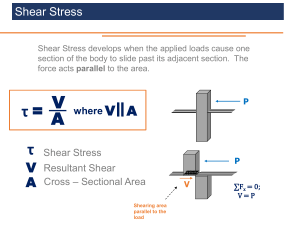
SRC-Pa-2000-Pujol-Transverse Reinforcement for Columns of RC Frames to Resist Earthquakes

TRANSVERSE REINFORCEMENT FOR COLUMNS
RESIST EARTHQUAKES
OF
RC FRAMES
TO
Downloaded from ascelibrary.org by INST TECN COSTA RICA on 10/06/15. Copyright ASCE. For personal use only; all rights reserved.
By Santiago Pujol,1 Mete Sözen,2 Member, ASCE, and Julio Ramı́rez,3 Member, ASCE
ABSTRACT: An approximate formulation to determine the amount of transverse reinforcement for columns of
reinforced concrete (RC) frames in seismic areas is presented. It is based on observations that suggested that
the main function of transverse reinforcement is to confine the core subjected to a complex state of stress rather
than simply resist shear or improve deformability under axial compression. The combined effects of shear and
axial stresses are assumed to be a function of the maximum drift ratio and they are interpreted using Coulomb’s
failure criterion. A comparison between results obtained with the model developed and current design recommendations suggests that the required amount of transverse reinforcement specified in ACI 318-95 can be reduced
safely for ‘‘flexible’’ columns (ratio of column height to effective depth ⬵6) under low amplitude displacement
cycles (ratio of lateral displacement to column height ⱕ3%) and ‘‘short’’ columns (ratio of column height to
effective depth ⬵4) under combinations of relatively low shear and axial stresses.
INTRODUCTION
A hypothesis for the resistance mechanism of reinforced
concrete (RC) columns subjected to shear reversals is proposed. The hypothesis is tested with the help of available data
and used to determine the transverse reinforcement requirement in earthquake resistant columns as a function of maximum axial and shear unit stresses, maximum drift ratio, and
the properties of the column.
The essential requirement for an RC column subjected to
strong ground motion is that it retain a substantial portion of
its strength as it experiences severe loading reversals into the
nonlinear range of response. Given a ground motion intensity,
column survival depends on a complex interaction of many
parameters such as the magnitudes of normal and shear
stresses, type and strength of the concrete, drift history, and
transverse reinforcement (its strength, configuration, and distribution). Because selection of the column dimensions and
material is driven by global design issues, the key design decision for column behavior is the selection of transverse reinforcement.
Design criteria for transverse reinforcement are currently
based on two different concepts of column behavior identified
originally by Blume et al. (1961). The first concept refers to
the rotation capacity in the potential hinging regions in the
column, usually assumed to be near column ends. The second
concept refers to shear failure. Both sets of criteria are based
on a mix of theory and experience. Strictly, they are unrelated.
The set of criteria to insure adequate rotation capacity is
based explicitly on the flexural theory. The limiting rotation is
related to the ratio of the limiting concrete compressive strain
and the depth to the neutral axis
␾u =
εu
c
Eq. (1) is intelligible if it is assumed that the strain distribution at a section of strain concentration and stress reversal
is linear and that the depth c can be determined a priori. Given
that, the relevant design requirement [exemplified by ACI 31895, Sections 21.4.4.1–5 (‘‘Building’’ 1995)] is sensible. Transverse reinforcement should increase the nominal strain capacity εu and decrease the depth c leading to improved rotation
capacity. Considering that both effects (increase of εu and decrease of c) are not well understood, the amount of transverse
reinforcement is selected in reference to a phenomenon only
remotely related to rotation capacity. As proposed by Richart
and Brown (1934) for ‘‘spiral’’ columns, the amount of transverse reinforcement is determined on the basis of compensating for the axial-load capacity of the column shell.
The set of design criteria related to shear strength of the
column starts with a simplifying concept for the maximum
shear force. Recognizing the difficulties in determining the actual maximum shear that a critical column may experience
during an earthquake, Blume et al. (1961) stated the maximum
column shear as
Vuf =
1
Res. Asst., School of Civ. Engrg., Purdue Univ., West Lafayette, IN
47907.
2
Kettelhut Distinguished Prof. of Struct. Engrg., Purdue Univ., West
Lafayette, IN.
3
Prof. of Struct. Engrg. and Asst. Head for Grad. Studies, School of
Civ. Engrg., Purdue Univ., West Lafayette, IN.
Note. Associate Editor: Brad Cross. Discussion open until September
1, 2000. To extend the closing date one month, a written request must
be filed with the ASCE Manager of Journals. The manuscript for this
paper was submitted for review and possible publication on March 2,
1999. This paper is part of the Journal of Structural Engineering, Vol.
126, No. 4, April, 2000. 䉷ASCE, ISSN 0733-9445/00/0004-0461–0466/
$8.00 ⫹ $.50 per page. Paper No. 20366.
(2)
where Vuf = column shear corresponding to the simultaneous
development of the anticipated maximum moments at both
ends of the columns, acting in the same sense; Mtop, Mbot =
column moment capacity at top and bottom ends of the column
(based on increased yield stress primarily to recognize strain
hardening in the reinforcement); and Lc = clear height of column.
The force determined by (2) is compared with the assumed
shear strength of the column defined as
(1)
where ␾u = limiting curvature, in units of 1/length; εu = limiting concrete compressive strain; and c = depth of neutral axis
at limit.
Mtop ⫹ Mbot
Lc
Vu = Vc ⫹ Vs
(3)
where Vu = shear strength of column; Vc = shear strength attributed to concrete; and Vs = shear strength attributed to transverse reinforcement.
The amount of transverse reinforcement is determined from
the condition
Vu ⱖ Vuf
(4)
It is important to note that both sets of design criteria are
based on the implicit assumption of column behavior under
monotonically increasing load. Nevertheless, to date there has
been no evidence from the field that the results are flawed.
From the laboratory, there has been plenty of evidence suggesting flaws in the implied assumptions and results of the two
sets of design criteria (Wight and Sozen 1973; Ang et al. 1989;
JOURNAL OF STRUCTURAL ENGINEERING / APRIL 2000 / 461
J. Struct. Eng., 2000, 126(4): 461-466
Saatcioglu and Ozcebe 1989; Wong et al. 1993; Xiao and Martirossyan 1998). Possibly because the process related to shear
strength is simple and direct, proposals to improve the design
requirements for columns have been made almost exclusively
in reference to shear. In this paper, a proposal is made to determine the required amount of transverse reinforcement on
the basis of a single hypothesis for concrete failure under combined effect of normal and shear stresses.
Downloaded from ascelibrary.org by INST TECN COSTA RICA on 10/06/15. Copyright ASCE. For personal use only; all rights reserved.
SCOPE
Because of the limits of experimental data essential for testing the proposed hypothesis, the scope of the study is limited
to RC columns with the slenderness ratio ␭ (ratio of length
between the points of contraflexure and fixity to the effective
depth of the column) from 1.9 to 3.5 and nominal unit shear
stresses v (ratio of maximum shear to cross-sectional area of
column core) from 0.5 to 1.1兹 f ⬘c MPa (6 to 13兹 f c⬘ psi). Data
from 29 columns tested with shear reversals in six different
investigations have been studied. All columns had rectilinear
sections and confined cores, and all concrete was cast using
normal-weight aggregate. The applied axial compressive load
ranged from 7 to 35% of nominal section capacity. The study
did not include elements without axial loads or with varying
axial load. Strain rate and time-dependent effects were not
dominant. The ranges of the experimental variables, including
load histories, are defined in Table 1 and Fig. 1.
In addition to the domain defined by the experimental variables, direct applicability of the results is limited to cases
satisfying the following conditions:
scribed by Wight and Sozen (1973) is shown in Fig. 2. It was
observed that yielding of the transverse reinforcement was the
defining event in the behavior of the test specimens. If the
transverse reinforcement did not yield, the column sustained
its strength under cyclic loading. If it yielded (Fig. 2), there
was a ‘‘racheting’’ increase of the strain in subsequent cycles,
and the column strength decayed.
Saatcioglu and Ozcebe (1989), in discussion of a series of
14 columns subjected to shear reversals, reported that ‘‘the
effect of constant axial load on hysteretic response of reinforced concrete columns is to reduce ductility and accelerate
stiffness and strength degradation.’’
Xiao and Martirossyan (1998) concluded from their tests of
six columns that an increase in axial load tended to reduce
toughness if the transverse reinforcement was approximately
one-half of that required by ACI 318-95. The reduction in
toughness with axial force was not observed in specimens with
transverse reinforcement satisfying ACI 318-95.
These three observations suggest that the quantification of
• The maximum column drift capacity is not less than the
drift at yield.
• Probable column shear Vuf exceeds the shear at inclined
cracking.
• The ‘‘static’’ shear capacity Vu is not less than the column
shear defined by (2).
• The column core is confined by transverse reinforcement.
• The governing drift cycles occur primarily in the plane
defined by one of the principal axes of the cross section.
SELECTED OBSERVATIONS FROM EXPERIMENTAL
STUDIES
In three of the studies considered, there were observations
that suggested that the main function of the transverse reinforcement is to confine the core subjected to a complex state
of stresses rather than simply resist shear or improve deformability under axial compression.
An example of the strain histories measured in transverse
reinforcement of columns subjected to shear reversals deTABLE 1.
Ranges of Variables Covered by Experimental Data
Variable
(1)
Symbol
(2)
Concrete compressive strength
f ⬘c
Longitudinal reinforcement yield
stress
Total reinforcement ratio
Unit strength of transverse reinforcement (Aw /bcs) fwy
Axial-load ratio P/Ag f c⬘
Slenderness ratio a/d
Unit shear stress ratio
fy
Maximum drift ratio ⌬max /a
Ratio of gross to core section
Ratio of axial to transverse unit
stress
␳
␳w fwy
␴n
␭
v /兹f c⬘
␥
Ag /Ac
␴a /␴t
Range
(3)
26–97 MPa
(3,700–14,000 psi)
338–510 MPa
(49,000–74,000 psi)
2.0–3.6%
1.7–9.7 MPa
(240–1,400 psi)
0.07–0.35
1.9–3.5
0.5–1.1 (MPa units)
(6–13; psi units)
1.0–9.4%
1.3–2.0
2.1–12.6
FIG. 1.
Ranges of Variables Covered by Experimental Data
462 / JOURNAL OF STRUCTURAL ENGINEERING / APRIL 2000
J. Struct. Eng., 2000, 126(4): 461-466
Therefore, forces normalized with respect to the core area
rather than local unit stresses are used to construct the circle.
The axial stress is approximated by
Downloaded from ascelibrary.org by INST TECN COSTA RICA on 10/06/15. Copyright ASCE. For personal use only; all rights reserved.
␴a =
P⫹T
hc ⭈ b c
(6)
where ␴a = mean axial compressive stress on the core; P =
applied axial load; T = force in the tensile reinforcement (approximated as 1/2 ⭈ As ⭈ fy for the test specimens); As = area of
longitudinal reinforcement; fy = longitudinal reinforcement
yield stress; hc = depth of core (measured center-to-center of
peripheral hoops); and bc = width of core (measured centerto-center of peripheral hoops).
The shear stress is approximated by
v=
V
hc ⭈ b c
(7)
where v = mean shear stress; and V = shear force.
The stress normal to the column axis and in the plane of
the applied shear is approximated as
␴t =
FIG. 2. Strains in Transverse Reinforcement of Column Subjected to Shear Reversals (Wight and Sozen (1973)
the required amount of transverse reinforcement is better made
on the basis of a direct combination of the normal and shear
stresses. The simplest framework for that approach is the Coulomb criterion.
COULOMB CRITERION
The conditions of failure for a tension-weak material subjected to combined effects of normal and shear forces are conveniently represented by Coulomb’s criterion (1773), illustrated in Fig. 3. Material failure is assumed to occur if line C
is transgressed by a Mohr’s circle representing a particular
combination of axial and shear stresses. Line C is defined by
vu = v0 ⫹ m␴
(5)
where vu = unit shear strength; v0 = ordinate of line representing Coulomb’s criterion at ␴ = 0; m = slope of line representing Coulomb’s criterion; and ␴ = unit stress acting perpendicular to the potential failure plane.
Mohr’s circle is a statement of equilibrium. Its use in reference to local failure of the concrete within the column core
requires accurate information about the distributions of the
normal and shear unit stresses; a requirement very difficult to
satisfy at the limiting stage of loading under shear reversals.
FIG. 3.
Coulomb’s Criterion
Aw fyw
s ⭈ bc
(8)
where ␴t = mean stress exerted on the concrete by the hoop
bars assumed to have yielded; Aw = cross-sectional area of
hoop bars in planes parallel to the shear plane at spacing s; fyw
= transverse reinforcement yield stress.
A limited amount of information is available to help define
the constants in (5). Considère (1903) used Coulomb’s criterion to explain the strength of concrete in spiral columns, and
Richart et al. (1929) stated Coulomb’s criterion in relation to
the strength of the concrete
vu = k1 ⭈ f ⬘c ⫹ k2 ⭈ ␴
(9)
Using data from tests of concrete confined by hydraulic
pressure, Richart et al. (1929) inferred that k1 ⬇ 1/4 and k2 ⬇
3/4 (for normal-weight aggregate concrete subjected to
monotonically increasing load).
To interpret the results of tests of RC columns subjected to
shear reversals, it is hypothesized that only k1 is susceptible to
change because of the cumulative effects of microcracks, and
that this cumulative effect must result from an interaction of
number N and extent ␥ of the loading cycles. A single excursion into the nonlinear range of response in either direction
represents the standard case. It is plausible to expect that subsequent excursions in the same direction will result in additional internal cracking of the intact concrete and, therefore,
may reduce the strength by a finite amount. The reduction in
strength should be a function of the extent of each displacement cycle such that the cumulative effect for a given number
of cycles increases with increasing displacement amplitude
(Fig. 4). To establish this hypothetical function in quantifiable
terms would require systematic testing of a large number of
columns. Within the limitations of the available experimental
FIG. 4. Idealized Relative Effects of Number N and Extent ␥ of
Loading Cycles
JOURNAL OF STRUCTURAL ENGINEERING / APRIL 2000 / 463
J. Struct. Eng., 2000, 126(4): 461-466
TABLE 2.
Specimen
(1)
␭
(2)
Ag /Ac
(3)
f ⬘c
MPa (psi)
(4)
2D16RS
2.3
1.35
32 (4,640)
CA025C
1.9
1.64
26 (3,740)
Experimental Data
P/ [ f c⬘ Ag]
(5)
As /Ag
(6)
␳w ⭈ fyw
MPA (psi)
(7)
0.020
0.024
v/兹 f c⬘
(8)
␥
(%)
(9)
2.1 (300)
7.3
3.8
4.4 (640)
13.0
2.5
6.8
6.3
8.0
8.0
7.8
4.0
5.1
9.0
9.0
8.8
(a) Ohue et al. (1985)
0.14
(b) Ono et al. (1989)
0.26
Downloaded from ascelibrary.org by INST TECN COSTA RICA on 10/06/15. Copyright ASCE. For personal use only; all rights reserved.
(c) Saatcioglu and Ozcebe (1989)
2
3
4
6
7
3.3
3.3
3.3
3.3
3.3
1.41
1.41
1.41
1.44
1.44
30
35
32
37
39
(4,380)
(5,050)
(4,640)
(5,410)
(5,660)
1
2
3
4
5
6
7
2.5
2.5
2.5
2.5
2.5
2.5
2.5
1.56
1.56
1.56
1.56
1.56
1.56
1.56
99
99
99
99
99
99
99
(14,400)
(14,400)
(14,400)
(14,400)
(14,400)
(14,400)
(14,400)
0.16
0.14
0.15
0.13
0.13
0.033
0.033
0.033
0.033
0.033
1.7
3.3
5.0
3.6
3.6
(240)
(480)
(720)
(520)
(520)
0.026
0.026
0.026
0.026
0.026
0.026
0.026
5.1
7.7
2.7
7.4
5.0
5.4
5.0
(740)
(1,110)
(390)
(1,080)
(730)
(790)
(730)
12.4
12.5
12.9
12.2
12.2
12.7
12.2
2.0
4.0
1.0
2.0
1.0
1.0
1.0
0.036
0.036
0.025
0.025
0.025
0.025
9.7
9.7
9.7
9.7
3.8
3.8
(1,410)
(1,410)
(1,410)
(1,410)
(550)
(550)
9.5
11.2
7.3
8.9
7.2
8.6
9.4
7.9
7.2
6.7
6.4
4.3
0.024
0.024
0.024
0.024
0.024
0.024
0.024
0.024
0.024
1.7
1.7
1.7
2.4
2.4
3.4
3.4
4.2
4.2
(250)
(250)
(250)
(355)
(355)
(500)
(500)
(612)
(612)
7.9
7.3
7.8
9.7
9.6
8.1
8.1
8.7
8.6
2.7
3.6
3.3
4.9
5.5
6.8
6.9
6.0
6.1
(d ) Sakai et al. (1990)
0.35
0.35
0.35
0.35
0.35
0.35
0.35
(e) Xiao and Martirossyan (1998)
19-T10-0.1P
19-T10-0.2P
16-T10-0.1P
16-T10-0.2P
16-T6-0.1P
16-T6-0.2P
2.3
2.3
2.3
2.3
2.2
2.2
1.35
1.35
1.35
1.35
1.31
1.31
76
76
86
86
86
86
(11,000)
(11,000)
(12,500)
(12,500)
(12,500)
(12,500)
40.033
25.033
3.5
3.5
3.5
3.5
3.5
3.5
3.5
3.5
3.5
2.00
2.00
2.00
2.00
2.00
2.00
2.00
1.91
1.91
34
34
34
26
26
33
33
36
36
(4,870)
(4,880)
(4,880)
(3,780)
(3,780)
(4,840)
(4,840)
(5,150)
(5,150)
0.10
0.20
0.10
0.19
0.10
0.19
( f ) Wight and Sozen (1973)
40.048
40.067
40.092
0.11
0.07
0.07
0.15
0.15
0.11
0.11
0.11
0.11
information, the reduction in k1 is interpreted in relation to
displacement only. In a previous study (Pujol 1997), the parameter ␥/␭ (where ␥ = maximum drift ratio—ratio of lateral
displacement to column height—reached before a reduction
in strength of more than 20%; and ␭ = ratio of the shear span
—distance between the points of fixity and contraflexure—to
the effective depth) was found to be suitable for normalizing
the drift capacity data from RC members subjected to cyclic
shear. The same parameter is used here.
EVALUATION OF EFFECT OF DRIFT RATIO ␥ ON k1
Data from 29 tests of RC columns from six different investigations (Wight and Sozen 1973; Ohue et al. 1985; Ono et al.
1989; Saatcioglu and Ozcebe 1989; Sakai et al. 1990; Xiao
and Martirossyan 1998) were used to evaluate the effect of the
ratio ␥/␭ on k1 [(9)]. Table 2 contains relevant properties and
test results for each specimen. The ranges of the variables
covered by the experimental data are included in Table 1 and
Fig. 1.
The values of k1 that satisfy the failure criterion discussed
previously, for the different load conditions corresponding to
each specimen studied, are plotted against the ratio ␥/␭ in Fig.
5. Despite the scatter, it can be seen that, for given dimensions
and boundary conditions, k1 tends to decrease with increasing
drift ratio ␥.
A reasonable lower bound for k1 is proposed here
FIG. 5.
k1 =
Effect of Drift Ratio ␥ on k1
1
7
冉
1⫺
冊
100 ␥
⭈
3 ␭
ⱖ0
(10)
It is important to notice that, in relation to Fig. 4, (10) represents a reasonable lower bound surface obtained by assuming a finite and constant effect of N.
The failure criterion illustrated in Fig. 3, can be expressed
as
464 / JOURNAL OF STRUCTURAL ENGINEERING / APRIL 2000
J. Struct. Eng., 2000, 126(4): 461-466
␴t 3
5
= ⭈ ␣ ⫹ 1 ⫺ ⭈ 兹␣2 ⫺ ␤2
␴a 8
8
(11)
where
Downloaded from ascelibrary.org by INST TECN COSTA RICA on 10/06/15. Copyright ASCE. For personal use only; all rights reserved.
␣=4
k1 ⭈ f ⬘c
⫹ 3;
␴a
␤=4
v
␴a
Eq. (11) is a rather inconvenient vehicle for design. The
labor involved in its use is not justified by its accuracy or by
its effect on the cost of the product. However, it is very useful
in obtaining a perspective of the relative influences of the critical design parameters.
Using the definition of ␴t in (8), (11) may be rearranged to
yield values for the required transverse reinforcement ratio ␳w
␳w =
冋
册
3
5
␴a
⭈ ␣ ⫹ 1 ⫺ ⭈ 兹␣2 ⫺ ␤2 ⭈
8
8
fyw
(12)
where ␳w = Aw/(s ⭈ bc), transverse reinforcement ratio.
For a combination of the governing parameters [␭ = 2.0,
␥ = 0.04, f c⬘ = 34 MPa (5,000 psi), fyw = 414 MPa (60,000
psi)], the solid curves in Fig. 6 indicate the variation of the
required values of ␳w with the unit axial compressive stress
(expressed as a function of cylinder strength) at three different
levels of the unit shear stress in the column core [0.5, 0.7, and
0.8兹f ⬘c MPa (6, 8, and 10兹f c⬘ psi)].
The variation of ␳w with axial and shear stresses for the case
of a more slender column (␭ = 3.0) under displacement cycles
FIG. 6. Variation of Required Transverse Reinforcement Ratio
␳w with Mean Axial and Shear Stresses (␭ = 2.0, ␥ = 4%)
with a lower maximum amplitude (␥ = 0.03) is indicated by
the solid curves in Fig. 7. In this case, the amount of transverse
reinforcement required to satisfy the condition in (4) controls
for low axial stresses. In (4), the shear strength of the column
Vu has been estimated using (3), in which the shear strength
attributed to the concrete Vc has been assumed to be
冉
Vc = 0.17 ⭈ 1 ⫹
冉
Vc = 2 ⭈ 1 ⫹
冊
␴a ⭈ Ac ⫺ T
⭈ 兹f ⬘c ⭈ (0.8 ⭈ Ag)
13.8 ⭈ Ag
冊
␴a ⭈ Ac ⫺ T
⭈ 兹f ⬘c ⭈ (0.8 ⭈ Ag)
2000 ⭈ Ag
(SI)
(13a)
(English system)
(13b)
where ␴a = mean axial compressive stress; Ac = core area; Ag
= gross section area (taken as 1.4 ⭈ Ac); and T = force in the
tensile reinforcement (assumed to be 0.015 ⭈ Ag ⭈ 414 MPa =
0.015 ⭈ Ag ⭈ 60,000 psi).
The horizontal, broken line in Figs. 6 and 7 indicates the
value of ␳w required by ACI 318-95, Section 21.4.4, on the
assumption that the ratio of the gross section area Ag to the
core area Ac is, again, 1.4. As specified by ACI 318-95, the
required amount is insensitive to the axial load and the shear.
Considering that a nominal maximum unit shear stress of
0.6兹f ⬘c MPa (7兹f c⬘ psi), based on the gross section area Ag,
is a desirable design limit (although higher values are permitted) and that this corresponds to approximately 0.8兹f ⬘c
MPa (10兹f ⬘c psi) on the core for the column considered, it is
reassuring to observe that the traditional requirement is not
found to be inadequate on the basis of the formulation presented. This coincidence does not rationalize the current approach used in Section 21.4.4 of ACI 318-95 but suggests that
the judgment used in developing it must have compensated for
the shortcomings of the concept. It must also be conceded that
the ACI result is obtained with less data and far less numerical
labor.
On the other hand, it is noted that the congestion created
by the ACI requirement of approximately 1% transverse reinforcement can be reduced safely for ‘‘flexible’’ columns (ratio of column height to effective depth ⬵6) under low amplitude displacement cycles (ratio of lateral displacement to
column height ⱕ3%) and ‘‘short’’ columns (ratio of column
height to effective depth ⬵4) under combinations of relatively
low shear and axial stress [v ⱕ 0.7兹f ⬘c MPa (8兹f c⬘ psi) ␴a ⱕ
0.45 ⭈ f c⬘). If found to be reasonable by the designer, increases
in column dimensions could justify a significant reduction in
transverse reinforcement.
CONCLUSIONS
Selection of the amount of transverse reinforcement for columns of RC frames in seismic areas may be based on the
relative effect of axial and shear forces, maximum drift ratio,
material properties, and column dimensions as indicated by
(10) and (12). As interpreted here (Figs. 6 and 7), these equations indicate that the current ACI requirement for transverse
reinforcement can be reduced safely for flexible columns under low amplitude displacement cycles and short columns under combinations of relatively low shear and axial stresses.
Use of the proposed formulation is limited to the ranges of
the experimental variables included in the study as described
in Table 1 and Fig. 1 and design conditions satisfying the
following assumptions:
FIG. 7. Variation of Required Transverse Reinforcement Ratio
␳w with Mean Axial and Shear Stresses (␭ = 3.0, ␥ = 3%)
• The maximum column drift capacity is not less than the
drift at yield.
• Column shear Vuf exceeds the shear at inclined cracking.
• The static shear capacity Vu is not less than the column
shear defined by (2).
JOURNAL OF STRUCTURAL ENGINEERING / APRIL 2000 / 465
J. Struct. Eng., 2000, 126(4): 461-466
• The column core is confined by transverse reinforcement.
• The governing drift cycles occur primarily in the plane
defined by one of the principal axes of the cross section.
The proposed procedure provides a new perspective to the
phenomenon of column behavior under shear reversals and
suggests that the required amount of transverse reinforcement
in earthquake resistant RC columns can be reduced by controlling the nominal axial and shear stresses.
Downloaded from ascelibrary.org by INST TECN COSTA RICA on 10/06/15. Copyright ASCE. For personal use only; all rights reserved.
APPENDIX I.
DERIVATION OF (11)
1. Express the radius of the Mohr circle ‘‘at failure’’ R as
a function of v0, ␴a, ␴t, and ␾ = tan⫺1 (m)
R = v0 ⭈ cos ␾ ⫹
1
(␴t ⫹ ␴a) ⭈ sin ␾
2
2. Express R as a function of v, ␴a, and ␴t
R=
冑
1
(␴a ⫺ ␴t)2 ⫹ v 2
4
3. Solving for ␴t after equating the last two expressions and
replacing ␾ by tan⫺1 (3/4)
3
17
5
␴t = ⭈ v0 ⫹
⭈ ␴a ⫺ ⭈ 兹[(4 ⭈ v0 ⫹ 3 ⭈ ␴a)2 ⫺ 16 ⭈ v 2]
2
8
8
4. Dividing by ␴a
␴t 3 v0
17
5
= ⭈ ⫹
⫺ ⭈
␴a 2 ␴a
8
8
冑冋冉
4⭈
v0
⫹3
␴a
冊
2
⫺ 16 ⭈
冉 冊册
v
␴z
2
5. Let ␣ = 4(v0/␴a) ⫹ 3 and ␤ = 4(v/␴a). Substituting these
terms in the last equation
␴t 3
5
= ␣ ⫹ 1 ⫺ 兹␣2 ⫺ ␤2
␴a 8
8
APPENDIX II.
REFERENCES
Ang, B. G., Priestley, M. J. N., and Paulay, T. (1989). ‘‘Seismic shear
strength of circular concrete columns.’’ ACI Struct. J., 86(1), 45–59.
Blume, J. A., Newmark, N. M., and Corning, L. H. (1961). Design of
multistory reinforced concrete buildings for earthquake motions. Portland Cement Association, Skokie, Ill.
‘‘Building code requirements for structural concrete.’’ (1995). ACI 31895, American Concrete Institute, Farmington Hills, Mich.
Considère, A. (1903). ‘‘Résistance à la Compression du Béton Armé and
du Béton Fretté.’’ Génie Civil, France (in French).
Coulomb, C. A. (1773). ‘‘Essai sur une Application des Règles de Maximis et Minimis à quelques Problèmes de Statique Relatifs à
l’Architecture.’’ Proc., l’Académie Royale des Sciences par divers savans, et lûs dans ses assemblées, Mémoires de Mathématique et de
Physique, Vol. 7, 343–382 (in French).
Ohue, M., Morimoto, H., Fujii, S., and Morita, S. (1985). ‘‘The behavior
of R.C. short columns failing in splitting bond shear under dynamic
lateral loading.’’ Trans. Japan Concrete Inst., Tokyo, 7, 293–300.
Ono, A., Shirai, N., Adachi, H., and Sakamaki, Y. (1989). ‘‘Elasto-plastic
behavior of reinforced concrete column with fluctuating axial force.’’
Trans. Japan Concrete Inst., Tokyo, 11, 239–246.
Pujol, S. (1997). ‘‘Drift capacity of reinforced concrete columns,’’ MS
thesis, Dept. of Civ. Engrg., Purdue University, West Lafayette, Ind.
Richart, F. E., Brandtzaeg, A., and Brown, R. L. (1929). ‘‘The failure of
plain and spirally reinforced concrete in compression.’’ Bull. No. 190,
University of Illinois Engrg. Experiment Station, 26(31), 52.
Richart, F. E., and Brown, R. L. (1934). ‘‘A study of reinforced concrete
columns.’’ Bull. No. 267, University of Illinois Engrg. Experiment Station, June.
Saatcioglu, M., and Ozcebe, G. (1989). ‘‘Response of reinforced concrete
columns to simulated seismic loading.’’ ACI Struct. J., 86(1), 3–12.
Sakai, Y., Hibi, J., Otani, S., and Aoyama, H. (1990). ‘‘Experimental study
on flexural behavior of reinforced concrete columns using high strength
concrete.’’ Trans. Japan Concrete Inst., Tokyo, 12, 323–330.
Wight, J. K., and Sozen, M. A. (1973). ‘‘Shear strength decay in reinforced concrete columns subjected to large deflection reversals.’’ Struct.
Res. Ser. No. 403, University of Illinois at Urbana-Champaign, Ill.
Wong, Y. L., Paulay, T., and Priestley, M. J. N. (1993). ‘‘Response of
circular reinforced concrete columns to multi-directional seismic attack.’’ ACI Struct. J., 90(2), 180–191.
Xiao, Y., and Martirossyan, A. (1998). ‘‘Seismic performance of highstrength concrete columns.’’ J. Struct. Engrg., ASCE, 124(3), 241–251.
466 / JOURNAL OF STRUCTURAL ENGINEERING / APRIL 2000
J. Struct. Eng., 2000, 126(4): 461-466