LABORATORIO 3 Ajuste de curvas

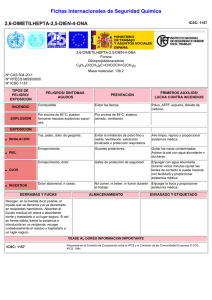
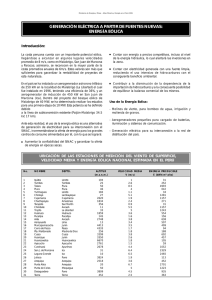
Ajuste de curvas
Método de mínimos cuadrados
Con los siguientes datos experimentales, realizar el ajuste de la curva aplicando el método de los
mínimos cuadrados
X
2
5
6
8
11
13
16
20
Y
3
5
7
9
11
14
17
19
Seguir el procedimiento del ejercicio 2 desde (a, b, c, d, e, f, g, h, i) y debe pronosticar en la
ecuación de la recta ajustada:
j) Calcular y’ si el valor de x=23 (Extrapolación hacia adelante)
k) Calcular y’ si el valor de x=-2 (Extrapolación hacia atrás)
1.0 PROCEDIMIENTO
a) Graficar la curva en papel milimétrico y = f(x)
b) Escribir la ecuación de la recta
y = a + bx
c) Calcular las constantes (a = ordenada en el origen y b = pendiente de la recta) utilizando las
siguientes formulas:
𝑎=
(∑ 𝑦)(∑ 𝑥 2 ) − (∑ 𝑥)(∑ 𝑥𝑦)
n(∑ 𝑥 2 ) − (∑ 𝑥)2
𝑏=
𝑛(∑ 𝑥𝑦) − (∑ 𝑥)(∑ 𝑦)
𝑛(∑ 𝑥 2 ) − (∑ 𝑥)2
d) Calcular las sumatorias y colocar en forma de tabla como se muestra a continuación
𝑥
2
5
6
8
11
13
16
20
𝑦
3
5
7
9
11
14
17
19
𝑥2
4
25
36
64
121
169
256
400
𝑥𝑦
6
25
42
72
121
182
272
380
∑ 𝑥 = 81
∑ 𝑦 = 85
∑ 𝑥 2 = 1075
∑ 𝑥𝑦 = 1100
e) Reemplazar los valores de las sumatorias en las fórmulas correspondientes y encontrar los
valores de a y b
𝑎=
(85)(1075) − (81)(1100)
8(1075) − (81)2
𝑎 = 1,1157
𝑏=
8(1100) − (81)(85)
8(1075) − (81)2
𝑏 = 0,9492
f) Reemplazar los valores de a y b en la ecuación de la recta
𝑦 ′ = 1,1157 + 0,9492𝑥
g) con esta ecuación diseñada, ajustar la grafica anterior; utilizando los mismos valores de x,
calcular los nuevos valores de y’
𝑦 ′ = 1,1157 + 0,9492 ∗ 2
𝑦 ′ = 3,0141
𝑦 ′ = 1,1157 + 0,9492 ∗ 5
𝑦 ′ = 5,8617
𝑦 ′ = 1,1157 + 0,9492 ∗ 6
𝑦 ′ = 6,8109
𝑦 ′ = 1,1157 + 0,9492 ∗ 8
𝑦 ′ = 8,7093
𝑦 ′ = 1,1157 + 0,9492 ∗ 11
𝑦 ′ = 11,5569
𝑦 ′ = 1,1157 + 0,9492 ∗ 13
𝑦 ′ = 13,4553
𝑦 ′ = 1,1157 + 0,9492 ∗ 16
𝑦 ′ = 16,3029
𝑦 ′ = 1,1157 + 0,9492 ∗ 20
𝑦 ′ = 20,0997
h) En la siguiente tabla, se presentan los valores de x y los nuevos valores de y’
X
2
5
6
8
11
13
16
20
Y’
3,0141
5,8617
6,8109
8,7093
11,5569
13,4553
16,3029
20,0997
g) Graficar los puntos de la tabla anterior, unir los mismos y el resultado es la recta de color rojo
que se muestra en el papel milimétrico (Volver a la gráfica de la página 1)
j) Calcular y’ si el valor de x=23 (Extrapolación)
𝑦 ′ = 1,1157 + 0,9492 ∗ 23
𝑦 ′ = 22,9473
k) Calcular y’ si el valor de x=-2 (Interpolación)
𝑦 ′ = 1,1157 + 0,9492 ∗ (−2)
𝑦 ′ = −0,7827
1.1 Extrapolar j) [23:22,9] y k) [-2: -0,7827] (volver a la gráfica de la página 1)
1.2 Utilizando computadora, graficar en Excel
x vs y // x vs y'
25
20
15
10
5
0
0
1.2.1
5
10
15
20
25
Extrapolar j) [23:22,9] y k) [-2: -0,7827] en Excel
x vs y // x vs y'
extrapolado
25
20
15
10
5
0
-5
0
-5
5
10
15
20
25