uvr&

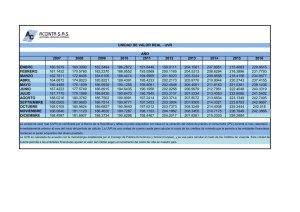
Sistema en Unidades
de Valor Real (Uvr)1
Ernesto Vélez Betancur
Jorge Ernesto Pérez Hernández
El Autor
Contador Público Titulado de la Universidad del Cauca,
Licenciado en Educación, especialidad Matemáticas
- Universidad del Cauca, Especialista en Gerencia
de Impuestos - Universidad del Cauca, Profesor de la
Facultad de Ciencias Contables, Económicas y Administrativas – Universidad del Cauca.
e-mail: evelez@unicauca.edu.co.
Economista de la Fundación Universitaria de Popayán,
Consultor del Poder Judicial en Procesos de Tipo Financiero, Catedrático Facultad de Ciencias Contables,
Económicas y Administrativas – Universidad del Cauca.
e-mail: pg01@hotmail.com
________________
1 Articulo tipo 1. Investigación científica
El presente artículo es resultado del proceso de investigación que los autores adelantan sobre el tema, Facultad
de Ciencias Contables, Económicas y Administrativas, Universidad del Cauca
250
Porik aN
Sistema en Unidades de Valor Real (Uvr)
Resumen
En el presente artículo se hace un breve recorrido sobre el origen de los
sistemas de financiación de vivienda en nuestro país: - La unidad de poder
adquisitivo constante (UPAC), la evolución de la fórmula de cálculo de
la corrección monetaria y los efectos que estos cambios generaron. - El
origen de la unidad de valor real (UVR) y la forma de calcularla. Finalmente
se explican y ejemplifican cada uno de las formas en UVR y en pesos,
aceptadas por la Superintendencia Bancaria, para la financiación de
vivienda.
Palabra Clave:
UPAC; UVR; corrección monetaria, capitalización y amortización.
Abstract
This article presents a brief summary of the origin of housing finance
systems in our country: - The unit of constant power of acquisition (UPAC),
the evolution of the formula to calculate the monetary correction and the
effects generated by these changes, and – the origin of the real value unit
(UVR) and the way it is calculated. Finally, each form in UVR and pesos
accepted by Superintendencia Bancaria for the financing of housing is
explained and exemplified.
Key Words:
UPAC; UVR; monetary correction, capitalization and amortization.
Recibido junio 5 2008
Aprobado junio 20 2008
Ernesto Vélez Betancur
Jorge Ernesto Pérez Hernández
Porik aN
251
1. Antecedentes
El sistema en unidades de valor real, es una alternativa que dentro del ordenamiento legal Colombiano, se creó para el financiamiento de créditos de
vivienda.
El sistema en unidades de valor real tuvo como origen la caída del antiguo
sistema de valor constante UPAC, en el año de 1999, causado por una serie de
sentencias de la Corte Constitucional que daban respuesta a las demandas que
contra el sistema de financiación de vivienda se instauraron en el país hacia
finales de los noventa. Al hacer una retrospectiva al sistema de valor constante,
sus inicios están enmarcados en el plan de desarrollo denominado Las Cuatro
Estrategias, presentado por el expresidente Misael Pastrana Borrero.
Las Cuatro Estrategias, como plan de desarrollo, contemplaban:
a.
b.
c.
d.
Impulso a la industria de la construcción.
Estimulo de las exportaciones de bienes diferentes al café.
Incremento de la productividad agrícola y la redistribución de la
propiedad rural.
Búsqueda de una mejor distribución y redistribución de los ingresos, mediante un sistema progresivo de impuestos.
El marco histórico de la creación de un sistema de financiación de vivienda
indexado, es decir, atado a la inflación, se fundamenta en la decadente productividad en el sector primario de la economía hacia finales de los años sesenta.
Sobre este particular, el profesor Lauchlin Currie, manifestó, con respecto a la
situación del país en ese entonces:
“..... Hay demasiada tierra bajo cultivo y demasiada gente dedicada a la
agricultura, cuyo ingreso medio es demasiado bajo.... la única solución
viable y económicamente defendible de los problemas (y oportunidades), que vienen junto con el progreso tecnológico en la Agricultura, es
la traslación de trabajo a actividades no agrícolas...” (Currie, 1968:47)
Consecuentemente con el planteamiento del Profesor Currie, se debe mencionar que la actividad de la construcción y la vivienda en general, se manifiestan como una necesidad básica de la población, mas aún, cuando en ese
momento, se presentaban fenómenos migratorios del campo hacia la ciudad,
252
Porik aN
Sistema en Unidades de Valor Real (Uvr)
de manera que, la iniciativa de impulsar la construcción como política de
desarrollo traía un doble beneficio, por un lado la generación de empleo y
ocupación para la población caracterizada por ser mano de obra no calificada y por otro lado, el fomento a las industrias generadoras de materiales de
construcción, las cuales a su vez se proveen de materia primas, que en su
mayoría son originarias del país.
El problema que se presentó en su momento con la iniciativa de impulsar la
construcción como política de desarrollo, fue la obtención de los recursos necesarios, ya que, dicha actividad requería recursos en gran cuantía los cuáles a
su vez no tenían disponibilidad presupuestal por parte del Estado. Cabe anotar
que hasta ese momento, en el país los recursos de financiación de crédito para
adquisición de vivienda eran escasos y básicamente canalizados a través del
Instituto de Crédito Territorial y el Banco Central Hipotecario.
La solución para la obtención de los recursos necesarios para impulsar la
industria de la construcción como Estrategia de Desarrollo, la planteó el
Profesor Currie al proponer la creación de agencias de renovación urbana
en las principales ciudades, con poderes amplios para adquirir tierras, con
la emisión de bonos, con cláusulas de ajuste con el costo de vida, lo cual fue
mas adelante puesto en vigencia. Esto en otras palabras es, sencillamente la
participación de la inversión privada en la financiación de vivienda a largo
plazo. De esta manera, se llega a la creación del sistema de valor constante
mediante el decreto 677 del 2 de mayo de 1.972; con el decreto 678 del 2 de
mayo del mismo año se da origen a las Corporaciones de Ahorro y Vivienda y
con el decreto 1229 del 17 de julio de 1.972, se estableció la Unidad de Poder
Adquisitivo Constante “ UPAC”.
En dicho sistema la Unidad de Poder Adquisitivo Constante UPAC, es un mecanismo para actualizar los dineros según la pérdida de poder adquisitivo de la moneda,
en términos de inflación, que dicho sea de paso, configura lo que desde el punto
de vista económico se conoce como las inflaciones Inerciales, entendida como
“…Capacidad de auto propagación de la inflación y practica generalizada de la indexación (corrección de los costos de los factores y de los
precios de los productos, indefinidamente), por los índices de inflación
anterior, para mantener la estructura relativa de precios, perpetuándose
de esta manera la inflación, incorporándose una tendencia al alza que
se va expandiendo y eleva el costo de los factores. La inflación inercial
Ernesto Vélez Betancur
Jorge Ernesto Pérez Hernández
Porik aN
253
presupone la convivencia con el proceso al alza , aceptado y practicado
por los agentes económicos, de manera tal que no se borra la memoria
inflacionaria, y se consolida lo que se denomina como la cultura inflacionaria, que aumenta la rigidez del proceso al alza…”( Paschoal, 2004:661)
Para entender el sistema de valor constante es importante describir cuales
fueron sus componentes:
Corrección monetaria: Es una tasa de interés efectiva anual, que al expresarla en forma periódica diaria, genera el porcentaje diario efectivo en el que
se reajusta la unidad UPAC, para cada uno de los días del mes de vigencia,
calculándose dicho porcentaje respecto de la unidad de poder adquisitivo
constante inmediatamente anterior.
UPAC: Es la unidad de poder adquisitivo constante que tiene como objetivo actualizar una cantidad de dinero determinada, en términos de la Corrección Monetaria.
Ejemplo del cálculo de la unidad UPAC: Para determinar el valor de la unidad
UPAC del día 02 de enero de 1.999, los datos que se requieren son:
• Corrección monetaria
=
• UPAC del primero de enero de 1999 =
26.63%. E. A.
$ 14.257.39
La corrección monetaria en este caso es la calculada por el Banco de la Republica expresada como una tasa de interés efectiva anual.
Para calcular la UPAC del día 02 de enero de 1.999, primero se calcula la tasa
de interés efectiva diaria que corresponde a la tasa efectiva anual a través de
la siguiente expresión:
Tasa de interés efectiva diaria = ( 1+ i ea ) (1 / 365) - 1
Al reemplazar el valor de la tasa de corrección monetaria se tiene:
i diario = ( 1 + 0 , 2663 ) ( 1 / 365 ) - 1
i diario = 0.00064706 , valor que al ser
expresado en forma porcentual queda: i diario = 0.064706 %
El valor de la UPAC del día inmediatamente anterior, en este caso, la del primero
de enero de 1.999 que era $14.257.39 se multiplica por el porcentaje obtenido:
$14.257.39 x 0.064706% = $ 9.225338
254
Porik aN
Sistema en Unidades de Valor Real (Uvr)
Este valor se suma a la UPAC del primero de enero de 1.999 obteniendo así
el valor de la UPAC del día 02 de enero de 1999: $14.257.39 + $9.225338 =
$ 14.266.62
En el anexo (1) se analiza la evolución de la metodología del cálculo de la
corrección monetaria determinada por el emisor, base del sistema de valor
constante UPAC, mientras éste estuvo vigente.
Como puede observarse en el anexo, la evolución de la fórmula de cálculo de
la corrección monetaria, base del sistema de valor constante UPAC, cambió en
su estructura en aspectos esenciales, considerados por su ideólogo, el Profesor
Currie, quien hablaba de valores indexados, es decir ligados a variación de
precios. (La negrilla es nuestra)
La iniciativa de colocarle un límite máximo al incremento de la corrección
monetaria, desde el punto de vista de un sistema de financiación indexado, generaba para los ahorradores una pérdida de poder adquisitivo de sus dineros, de
otra parte esta medida, aplicada en los inicios del sistema, logró la estabilidad
del mismo, por cuanto en situaciones de inflación elevada, el riesgo de que
los ingresos de los deudores no abarcara suficientemente estos incrementos
por efecto de la inflación y el incumplimiento en la atención a la deuda, se
compensaban con el límite determinado para la corrección monetaria. En este
sentido, es importante anotar que, la base de la actividad de intermediación
financiera se fundamenta en la consecución de activos de cartera sanos.
El procedimiento de cálculo de la corrección monetaria, como se observa en
el cuadro que resume su metodología, transformó la base de su cálculo con
fundamento en variación de precios y dirigido a la conservación de una cartera
sana, a un sistema de cálculo basado en indicadores de rentabilidad (CDT)
y con referente hacia los instrumentos de captación de los intermediarios financieros, terminó por generar un desequilibrio del sistema de financiación de
vivienda, y complementariamente afectó el incremento en el comportamiento
de las tasas de interés, lo que se puede corroborar al analizar la evolución
de la tasa de interés bancario certificada por la Superintendencia Bancaria2.
2
Es pertinente mencionar que, en el rango de tiempo comprendido entre el año
1972 y el año 1999 se financiaron créditos en UPAC y en pesos, los créditos en
________________
2 Hoy: Superintendencia Financiera de Colombia.
Ernesto Vélez Betancur
Jorge Ernesto Pérez Hernández
Porik aN
255
pesos a su vez se financiaron con sistemas de tasa flotante (combinadas) y tasa
fija y con sistemas de gradientes exponenciales. Para el caso de los créditos
con tasas flotantes o variables, estos eran operados utilizando la DTF3, como
tasa de referencia más puntos adicionales.
La DTF, se calcula con base en el promedio de las tasas de interés para los
depósitos a término fijo pactados a noventa días.
La DTF se calculaba para cada semana y tomaba para dicho cálculo los datos
suministrados por la Superintendencia Bancaria de los informes periódicos de
las entidades financieras.
A partir del Decreto 678 de 1972, se creó el sistema de valor constante, es decir
el sistema UPAC como mecanismo de financiación de vivienda a largo plazo;
en 1.991 dentro del Plan de Desarrollo denominado “La Revolución Pacifica”,
plan liderado por el expresidente César Gaviria Trujillo para el periodo 19901994, dentro de sus propuesta se encontraba la de “ abandonar el creciente
intervencionismo del Estado que cada vez más, era intervensionista directo,
juez y parte de las decisiones Económicas...” (Londoño, 1993:479)
Dentro de este marco conceptual y con el ánimo de darle mayor competitividad
al sector financiero y específicamente a las entidades que financiaban crédito
para adquisición de vivienda a largo plazo, se autorizó el crédito en pesos o
moneda legal adicionada a la DTF.
Sobre este tipo de créditos ligados a la DTF, hay que anotar que, al unir la
corrección monetaria a la DTF y permitir la financiación de créditos en DTF,
las tasas de interés del mercado, en este caso las tasas de los certificados de
depósito a término fijo de noventa días, se convierten en el referente único
para determinar el comportamiento, no solo del valor de las cuotas de las
obligaciones pactadas en estos sistemas de amortización, sino también del
comportamiento de los saldos de capital.
Para el sistema de financiación de vivienda, el cambio en la metodología del
cálculo de la corrección monetaria determinó que frente a las demandas que
se instauraron contra el sistema se tomaran las siguientes decisiones:
________________
3 Tasa de interés de referencia para operaciones de captación en Colombia
256
Porik aN
Sistema en Unidades de Valor Real (Uvr)
1.
Mediante Sentencia del Consejo de Estado 9280, se declara la
nulidad de la Resolución No 018 de Junio de 1995 del Banco de la
Republica, la cuál permitía el cálculo de la Corrección Monetaria
como el 74% del promedio móvil de la DFT de las cuatro semanas
anteriores a la fecha de cálculo.
2.
Por sentencia No C - 383 de la Corte Constitucional, se declara la
inexequibilidad de la Ley 31 de 1992, que permitía al Banco de la
Republica calcular la corrección monetaria con base en las tasas
de interés de la economía.
3.
Por sentencia C-700, de la Corte Constitucional se declara la
inexequibilidad, del Decreto 663 del Estatuto Orgánico del Sistema Financiero, el cuál era el que estructuraba el sistema de
Financiación de Colombia, hasta ese momento.
4.
Por sentencia C-747 de la Corte Constitucional, se declara inexequible el artículo 121, del Decreto 663 de 1993, es decir se prohíbe
específicamente la utilización de Sistema de Amortización que
capitalice intereses (La negrilla es nuestra) para créditos destinados a la financiación de vivienda.
5.
El 23 de diciembre de 1999, cobra vigencia la Ley Marco 546,
que crea el marco normativo concerniente a la financiación de
vivienda.
6.
Mediante Circular Externa No 068 del 13 de Septiembre de
2000, la Superintendencia Bancaria, especifica los sistemas de
amortización que en Colombia pueden utilizar los intermediarios
Financieros, para otorgar créditos destinados a la financiación de
vivienda.
7.
La circular Externa No 085 del 29 de diciembre la Superintendencia Bancaria, amplia el contenido de la circular 068 de 2000,
determinando el método para calcular la UVR y el ámbito de
aplicación del sistema especializado de financiación de vivienda
del que trata la Ley 546 de 1999.
Ernesto Vélez Betancur
Jorge Ernesto Pérez Hernández
Porik aN
257
2. Sistemas de Amortización Aprobados
por la Superintendencia Bancaria
Antes de entrar a estudiar los sistemas de amortización de los créditos para vivienda, es importante conocer el origen legal de la metodología del cálculo de la
UVR y aprender a aplicarla ya que en algunos de ellos es necesaria su utilización.
Cálculo de la UVR: En la Resolución Externa No 13 del 11 de agosto de 2.000
de la Junta Directiva del Banco de la República, se establece que el valor de la
unidad de valor real (UVR), de que trata el artículo 3 de la ley 546 de 1999 se
determinará diariamente durante el periodo de cálculo4, mediante la expresión:
UVRt = UVR15*(1 + i )t/d, donde:
UVRt: Valor en moneda legal colombiana de la UVR del día t del periodo del
cálculo.
UVR15: Valor en moneda legal colombiana de la UVR el día 15 de cada mes.
i: Variación mensual del índice de precios al consumidor certificada por el
DANE durante el mes calendario inmediatamente anterior al mes del inicio
del período de cálculo.
t: número de días calendario transcurridos desde el inicio del período de cálculo
hasta el día de cálculo de la UVR. Por lo tanto, t tendrá valores entre 1 y 31,
de acuerdo con el número días calendario del respectivo período de cálculo.
d: Número de días calendario del respectivo período de cálculo.
El cálculo y difusión de la UVR, los hará el banco de la República, en forma
mensual, para cada uno de los días del período de cálculo, informando con la
misma periodicidad, su valor en moneda legal de acuerdo con la metodología
establecida en la resolución.
Ejemplo de cálculo de la UVR.
________________
4 Es el periodo comprendido entre el día 16 inclusive, de un mes hasta el día 15, inclusive, del mes siguiente
258
Porik aN
Sistema en Unidades de Valor Real (Uvr)
Calcular la unidad de valor real para el 16 y 17 de mayo de 1999 con los siguientes datos:
Variación mensual del IPC abril de 1999 = 0,78%
UVR del 15 de Mayo de 1999
UVRt
= UVR15 (1 + i )
= 100.0000
⎛ t ⎞
⎜ ⎟
⎝d ⎠
Reemplazando:
€
a) UVR16-05-99 = 100.0000 (1 + 0,0078 )
b) UVR17-05-99 = 100.0000 (1 + 0,0078 )
⎛ 1 ⎞
⎜
⎟
⎝ 31 ⎠
⎛ 2 ⎞
⎜
⎟
⎝ 31 ⎠
= 100,0251
= 100,0501
€
La Superintendencia Bancaria, con base en la premisa de que todos los sistemas
de amortización, sean éstos en UVR o en pesos, deben cumplir las condiciones
€
de tasa fija por todo el plazo y la no capitalización5 de intereses (la negrilla
es nuestra) establecidos en la Ley 546 de 1999, aprobó los sistemas que se
describen en seguida agrupados así:
Cuota Constante en UVR
Amortización Constante a capital en UVR
SISTEMAS EN UVR
Cuota decreciente mensualmente en UVR
cíclica por períodos anuales.
Cuota Constante
SISTEMA EN PESOS
Amortización Constante a capital
Consideremos en detalle cada uno de ellos.
________________
5 Lo cuál resulta contradictorio, ya que los sistemas actualmente aplicados para financiación de vivienda están estructurados en Interés Compuesto.
Ernesto Vélez Betancur
Jorge Ernesto Pérez Hernández
Porik aN
259
2.1. Sistemas en Uvr
2.1.1. Cuota Constante en Uvr (Sistema de Amortización Gradual)
La cuota mensual es constante en UVR por todos los meses del plazo del crédito.
Se calcula como una anualidad uniforme en UVR a la tasa sobre UVR pactada
y por los meses del plazo mediante la siguiente fórmula:
R = A ( i sp ) / (1 – (1 + i sp) – n )
Donde:
R = Cuota mensual en UVR
A = Valor del préstamo en UVR, el cual resulta de dividir el valor del capital
en pesos entre la UVR del día de inicio de la operación de crédito.
n = Plazo en meses
i sp = tasa efectiva mensual equivalente a la tasa remuneratoria efectiva anual
( iea )
i sp = (( 1+iea ) (1/12)) - 1
Con respecto a la tasa de interés, se debe tener en cuenta que, la tasa con la
que se hace el cálculo de la cuota en UVR, se hace con los puntos fijos ya que la
tasa variable se aplica en la medida que la UVR se reajusta diariamente con la
tasa de inflación, por ello las cuotas en pesos variarán en la misma proporción.
De igual manera, aunque el saldo de la deuda valorada en UVR es siempre
decreciente, igual que en una anualidad en pesos, al convertirlo a pesos normalmente crece durante aproximadamente las dos terceras partes del plazo.
Ejemplo. Determinar el valor de la cuota en UVR, su equivalente en pesos y
elaborar las respectivas tablas a partir de los supuestos (Supuestos con los que
se trabaja en la Circular externa 068 de septiembre 13 de 2000 de la antigua
Superintendencia Bancaria) que a continuación se plantean:
Capital en Pesos: $1.000.000, UVR inicial: 111.3366, iea: 13.00%,
260
Porik aN
Sistema en Unidades de Valor Real (Uvr)
Inflación proyectada
: 10.00%, Plazo en meses: 60, Plazo en años: 5
Solución: Se expresa el valor de la deuda en UVR:
A = 1.000.000 / 111.3366
A = 8.981,772391
A = 8.981,7724 UVR
Se calcula la tasa de interés para el mes:
i = (1 + i sp) m – 1
0,13 = (1 + i m) 12 – 1
1,13 = (1 + i m) 12
1,13 1/12 = 1 + i m
1,01023684 – 1 = i m
i m = 0,01023684
Reemplazando en: R = A (i sp ) / [1 – (1 + i sp ) – n], se tiene:
R = 8.981,7724 (0,01023684) / [1 – (1 + 0,01023684) – 60] =
R = 91,94496698 / 0,45723992
R = 201,0869
Rta: El valor de la cuota constante es de 201,0869 UVR
Para elaborar la tabla de amortización se realizan los siguientes pasos:
1.
2.
Primer registro: n = 0, el saldo de la deuda en UVR es 8.981,7724
Segundo registro: n = 1, la cuota es 201,0869,
El interés se obtiene al multiplicar el saldo inmediatamente anterior de la
deuda por la tasa de interés mensual así: 8.981,7724 x 0,01023684 = 91,9449.
La amortización se obtiene al restarle a la cuota el interés: 201,0869 – 91,9449
= 109,1420
El nuevo saldo es la diferencia entre el saldo anterior y la amortización:
8.981,7724 - 109,1420 = 8.872,6304
Ernesto Vélez Betancur
Jorge Ernesto Pérez Hernández
3.
Porik aN
261
Para cada una de los registros siguientes se realiza el mismo procedimiento del paso 2.
Tabla 2.1.1. Cuota constante en Uvr.
n
0
1
2
3
4
…
(Fuente:
CUOTA
INTERES
AMORTIZACION
201,0869
201,0869
201,0869
201,0869
91,9449
90,8276
89,6989
88,5587
109,1420
110,2593
111,3880
112,5282
SALDO
8.981,7724
8.872,6304
8.762,3711
8.650,9831
8.538,4549
UVR
111,3366
112,2244
113,1192
114,0212
114,9304
Circular externa 068 del 13 de septiembre de 2000 de la antigua Superin-
tendencia Bancaria)
2.1.1.1. Cuota Equivalente en Pesos
Para encontrar la cuota equivalente en pesos y elaborar la tabla respectiva se
procede de la siguiente manera:
1.
Se calcula la tasa de interés mensual que equivale a la tasa de
inflación proyectada mediante la expresión:
i = (1 + i sp) m – 1
0,10 = (1 + i m) 12 – 1
1,10 = (1 + i m) 12
1,10 1/12 = 1 + i m
1,00797414 – 1 = i m
i m = 0,00797414
2.
Para el primer registro: n = 0 y para el saldo se multiplica el saldo
inicial de la deuda en UVR por el valor de la UVR al inicio del
crédito: 8.981,7724 x 111,3366 = 1.000.000
3.
Para el segundo registro se encuentra la nueva UVR, al multiplicar
el valor anterior de la UVR por la tasa de interés incrementada en
1: 111,3366 x 1,00797414 = 112,2244.
Con este nuevo valor de la UVR se encuentran la cuota, los intereses, la amortización y el saldo al multiplicarlo por el correspondiente valor en la tabla.
262
Porik aN
Sistema en Unidades de Valor Real (Uvr)
4.
Para cada uno de los siguientes registros se procede de manera
similar al paso 3.
Tabla 2.1.1.1. Cuota constante equivalente en pesos
UVR
n
CUOTA
INTERES
AMORTIZACION
SALDO
111,3366
0
1.000.000
112,2244
1
22.566,8567 10.318,4612 12.248,3954
995.725,6230
113,1192
2
22.746,7892 10.274,3454 12.472,4438
991.193,4089
114,0212
3
22.928,1696 10.227,5762 12.700,5934
986.395,4742
114,9304
4
23.110,9978
10.178,0868 12.932,9110
981.328,0370
…
…
(Fuente: Circular externa 068 del 13 de septiembre de 2000 de la antigua Superintendencia Bancaria)
2.1.2. Amortización Constante a Capital en Uvr
Durante cada uno de los meses del plazo se amortiza a la deuda una cantidad
uniforme en UVR igual al valor del préstamo en UVR dividido por el plazo en
meses. La cuota mensual a pagar es la amortización constante más los intereses
del mes sobre el saldo insoluto.
La cuota para cada mes se obtiene de aplicar la siguiente fórmula:
Ctu = A / n + ( St–1 . i sp )
Donde:
Ctu = Cuota en UVR a la altura t, t=1,2,3.....n
A = Valor de la deuda en UVR
St–1 = saldo a la altura t-1 igual a A – [(t – 1)(D / n)]
isp = tasa efectiva mensual equivalente = ((1+iea) (1/12))-1, iea tasa efectiva anual
remuneratoria sobre UVR
n = Número de meses del plazo
D = Saldo de la deuda en UVR en el momento t-1
De esta forma, la cuota mensual en UVR es decreciente pero variable en pesos
en una proporción inferior al IPC.
Ejemplo. A partir de los supuestos planteados en el caso anterior determinar el
valor de la cuota en UVR, su equivalente en pesos y elaborar las respectivas tablas.
Ernesto Vélez Betancur
Jorge Ernesto Pérez Hernández
Porik aN
263
Solución: Se expresa el valor de la deuda en UVR:
1.000.000 / 111,3366 = 8.981,772391 = 8.981,7724 UVR
Se calcula:
-La tasa efectiva mensual:
i = (1 + i sp) m – 1
0,13 = (1 + i m) 12 – 1
1,13 = (1 + i m) 12
1,13 1/12 = 1 + i m
1,01023684 – 1 = i m
i m = 0,01023684
-El saldo en el momento t – 1 mediante la expresión: St–1 = A – [(t – 1)(D/n)]
Como es en el primer momento, entonces:
St–1 = 8.981,7724 – [(1 – 1)( 8.981,7724/60)]
St–1 = 8.981,7724
Reemplazando en Ctu = A / n + ( St–1 . i sp ), se tiene:
Ctu = 8.981.7724 / 60 + ( 8.981,7724 x 0,01023684)
Ctu =149,6962066 + 91,94496698
Ctu= 241,6411735
Rta: El valor de la cuota es de 241,6411 UVR
Para elaborar la tabla de amortización se realizan los siguientes pasos:
1.
2.
Primer registro: n = 0, el saldo de la deuda en UVR es 8.981,7724
Segundo registro: n = 1, la cuota es 241,6411
El interés se obtiene al multiplicar el saldo inmediatamente anterior de la
deuda por la tasa de interés mensual así: 8.981,7724 x 0,01023684 = 91,9449
La amortización como es constante, se obtiene al dividir el total de la deuda
en UVR entre el número de periodos en que se va a cancelar:
8.981,7724 / 60 = 149,6962066 = 149,6962
264
Porik aN
Sistema en Unidades de Valor Real (Uvr)
El nuevo saldo es la diferencia entre el saldo anterior y la amortización:
8.981,7724 - 149,6962 = 8.832,0762
3.
Tercer registro: n = 2, en este caso es necesario encontrar nuevamente
el valor de la cuota a partir de la nueva información que se tiene:
A = 8.891,7724, i sp = 0,01023684, n = 59, D = 8.832,0762, St–1 =?, Ctu =?
Se halla primero St–1= A – [(t – 1)(D/n)]
St–1 = 8.891,7724 – [(2–1)(8.832,0762/59)]
St–1 = 8.981,7724 – (1)(149,6962067)
St–1 = 8.832,076193
Ahora se halla Ctu = A / n + ( St–1 . i sp )
Ctu = 8.981,7724 / 60 + ( 8.832,076193. 0,01023684 )
Ctu = 149,6962066 + 90,41255086
Ctu = 240,1087574
Para el valor de los intereses, la amortización y el nuevo saldo se procede igual
que en el paso 2.
4.
Para cada una de los registros siguientes se realiza el mismo procedimiento del paso 3.
Tabla 2.1.2. Amortización constante a capital en Uvr.
N
0
1
2
3
4
…
(Fuente:
CUOTA
INTERES
AMORTIZACION
241,6411
240,1087
238,5763
237,0439
91,9449
90,4125
88,8801
87,3477
149,6962
149,6962
149,6962
149,6962
SALDO
8.981,7724
8.832,0762
8.682,3800
8.532,6838
8.382,9876
UVR
111,3366
112,2244
113,1192
114,0212
114,9304
Circular externa 068 del 13 de septiembre de 2000 de la antigua Superintendencia
Bancaria)
2.1.2.1. Cuota Equivalente en Pesos
Para encontrar la cuota equivalente en pesos y elaborar la tabla respectiva se
procede de la siguiente manera:
Ernesto Vélez Betancur
Jorge Ernesto Pérez Hernández
1.
Porik aN
265
Se calcula la tasa de interés mensual que equivale a la tasa de
inflación proyectada mediante la expresión:
i = (1 + i sp) m – 1
0,10 = (1 + i m) 12 – 1
1,10 = (1 + i m) 12
1,10 1/12 = 1 + i m
1,00797414 – 1 = i m
i m = 0,00797414
2.
Para el primer registro: n = 0 y para el saldo se multiplica el saldo
inicial de la deuda en UVR por el valor de la UVR al inicio del
crédito: 8.981,7724 x 111,3366 = 1.000.000
3.
Para el segundo registro se encuentra la nueva UVR, al multiplicar
el valor anterior de la UVR por la tasa de interés incrementada en
1: 111,3366 x 1,00797414 = 112,2244.
Con este nuevo valor de la UVR se encuentran la cuota, los intereses, la amortización y el saldo al multiplicarlo por el correspondiente valor en la tabla.
4.
Para cada uno de los siguientes registros se procede de manera
similar al paso 3.
Tabla 2.1.2.1. Amortización constante a capital en pesos.
UVR
n
CUOTA
111,3366
0
112,2244
1
27.118,0274
113,1192
2
27.160,9040
114,0212
3
27.202,7560
114,9304
4
27.243,5502
…
…
(Fuente: Circular externa 068 del
INTERES
AMORTIZACION
10.318,4612
10.227,3896
10.134,2156
10.038,9061
16.799,5662
16.933,5143
17.068,5403
17.204,6441
SALDO
1.000.000
991.174,4522
982.143,8796
972.906,8460
963.460,1180
13 de septiembre de 2000 de la antigua Superin-
tendencia Bancaria)
2.1.3. Cuota decreciente mensualmente en UVR cíclica por períodos anuales.
Las cuotas mensuales durante cada año (aniversario) del crédito son decrecientes en UVR. Para cada período anual del crédito se repite la serie de doce
266
Porik aN
Sistema en Unidades de Valor Real (Uvr)
cuotas decrecientes. El decremento anual equivalente debe ser igual a la
inflación proyectada y no podrá modificarse durante el plazo.
Algebraicamente, la relación de equivalencia en este sistema de amortización
esta dada por la siguiente ecuación:
A = R {[(1 + isp)n – ( 1 – G )n ] / (G + i sp)} {[(1 + i ea )E – 1] / i ea(1 + i ea )E }
Donde:
A = Valor de la Deuda en UVR
R = Cuota del primer mes de cada año del crédito en UVR
isp = Tasa periódica fija del crédito
n = 12 cuotas mensuales
G = Decrecimiento porcentual de las cuotas, equivalente a la inflación
proyectada:
G =(1+Inf ) 1/12 -1
iea = Tasa efectiva anual remuneratoria sobre UVR, equivalente a la tasa mensual fija del crédito.
E = Número de años de la obligación.
Nota: Para la construcción de la tabla de amortización, se despeja R en la
ecuación dada, se construye la serie para los 12 primeros meses y la secuencia
se repite para el número de años de financiación del crédito.
Ejemplo. A partir de los supuestos planteados en el Sistema de Cuota Constante
en UVR, determinar el valor de la primera cuota de cada año, su equivalente
en pesos y elaborar las respectivas tablas.
Solución: Se expresa el valor de la deuda en UVR:
1.000.000 / 111,3366 = 8.981,772391 = 8.981,7724 UVR
Se calcula:
-La tasa efectiva mensual: i = (1 + i sp) m – 1
0,13 = (1 + i m) 12 – 1
1,13 = (1 + i m) 12
1,13 1/12 = 1 + i m
1,01023684 – 1 = i m
i m = 0,01023684
Ernesto Vélez Betancur
Jorge Ernesto Pérez Hernández
Porik aN
267
-El decrecimiento porcentual de las cuotas:
G = ( 1 + Inf ) 1/12 -1
G = (1+0,10 ) 1/12 -1
G = 1,00797414 – 1
G = 0,00797414
Reemplazando en
A = R{[(1 + isp)n – (1 – G)n ]/(G + i sp)}{[(1 + i ea )E – 1] / i ea(1 + i ea )E }
Se tiene:
8.981,7724 = R{ [(1 + 0,01023684)12 – (1 – 0,00797414)12 ] / (0,00797414 +
0,01023684)}
x { [(1 + 0,13)5 – 1] / 0,13(1 + 0,13)5 }
8.981,7724 = R{[1,13–0,90839748]/0,01821098} x {[1,84243518–1]/0,23951657}
8.981,7724 = R {12,16862135} x {3,51723131}
8.981,7724 = R x 42,79985601
R = 8.981,7724 / 42,79985601
R = 209,8552013
R = 209,8552
Rta: El valor de la primera cuota del ciclo es de 209,8552 UVR
Para elaborar la tabla de amortización se realizan los siguientes pasos:
1.
2.
Primer registro: n = 0, el saldo de la deuda en UVR es 8.981,7724
Segundo registro: n = 1, la primera cuota es 209,8552
El interés se obtiene al multiplicar el saldo inmediatamente anterior de la
deuda por la tasa de interés mensual así: 8.981,7724 x 0,01023684 = 91,9449
La amortización se obtiene al restarle a la cuota el interés:
209,8552 – 91,9449 = 117,9103
El nuevo saldo es la diferencia entre el saldo anterior y la amortización:
8.981,7724 - 117,9103 = 8.863,8621
3.
Tercer registro: n = 2, como la cuota se modifica hasta la cuota 12,
para empezar a repetirse a partir de la cuota 13, se debe buscar el
valor de la cuota que sigue; para obtenerla se multiplica la cuota
268
Porik aN
Sistema en Unidades de Valor Real (Uvr)
anterior por la unidad disminuida en el porcentaje de decrecimiento (G), así:
209,8552 (1– 0,00797414) =
209,8552(0,99202586) =
208,1817852 = 208,1817
Para el valor de los intereses, la amortización y el nuevo saldo se procede igual
que en el paso 2.
4.
Para cada una de los registros siguientes hasta el 12 se realiza el
mismo procedimiento del paso 3.
5.
A partir del registro 13 se empiezan a repetir las cuotas hasta la
cuota 24 y el interés, la amortización y el saldo se siguen calculando como en el paso 2.
6.
Para cada ciclo que sigue se realiza el mismo procedimiento del
paso 5.
Tabla 2.1.3. Amortización con cuota decreciente
mensualmente en Uvr cíclica por años.
n
CUOTA
INTERES
AMORTIZACION
SALDO
UVR
0
8.981,7724
111,3366
1
209,8552
91,9449
117,9103
8.863,8621
112,2244
2
208,1817
90,7379
117,4438
8.746,4183
113,1192
3
206,5216
89,5356
116,9860
8.629,4323
114,0212
4
204,8747
88,3381
116,5366
8.512,8957
114,9304
…
(Fuente: Circular externa 068 del 13 de septiembre de 2000 de la antigua Superintendencia Bancaria)
2.1.3.1. Cuota Equivalente en Pesos
Para encontrar la cuota equivalente en pesos y elaborar la tabla respectiva se
procede de manera similar a la realizada en los dos sistemas anteriores:
Se calcula la tasa de interés para el subperiodo, el saldo inicial de la deuda
en UVR, se calcula la nueva UVR, la cuota, los intereses, la amortización y el
nuevo saldo:
Ernesto Vélez Betancur
Jorge Ernesto Pérez Hernández
Porik aN
269
i m = 0,01023684, P = 1.000.000, UVR = 111,3366, UVR1 = 112,2244
Cuota = 209,8552
Cuota1
= 209,8552 x 112,2244 = 23.550,8739
Intereses1
= 91,9449 x 112,2244 = 10.318,4612
Amortización1 = 117,9103 x 112,2244 = 13.232,4126
Saldo1
= 8.863,8621 x 112,2244 = 994.741,6058
Tabla 2.1.3.1. Amortización con cuota decreciente mensualmente
en Uvr cíclica por años equivalente en pesos.
UVR
n
111,3366
0
112,2244
1
113,1192
2
114,0212
3
114,9304
4
…
…
(Fuente: Circular
CUOTA
INTERES
AMORTIZACION
23.550,8739
23.549,3473
23.547,8406
23.546,3312
10.318,4612
10.264,1986
10.208,9565
10.152,7331
13.232,4126
13.285,1487
13.338,8841
13.393,5980
SALDO
1.000.000
994.741,6058
989.387,8409
983.938,2261
978.390,5079
externa 068 del 13 de septiembre de 2000 de la antigua Superin-
tendencia Bancaria)
2.2. Sistema En Pesos
2.2.1. Cuota Constante (Amortización Gradual en pesos)
La cuota mensual es fija en pesos por todo el plazo del crédito. Se calcula como
una anualidad uniforme ordinaria.
R = A (i sp ) / [1 – (1 + i sp ) – n]
Donde:
R = Cuota mensual en pesos.
A = Valor del préstamo en pesos.
n = Plazo en meses
isp = tasa efectiva mensual equivalente a la tasa remuneratoria efectiva anual iea ,
isp = ((1+i ea ) (1/12))-1
Ejemplo. A partir de los mismos supuestos con los que se ha trabajado en los
sistemas anteriores y con una tasa de corrección monetaria del 8%, determinar
el valor de las cuotas y elaborar la respectiva tabla.
270
Porik aN
Sistema en Unidades de Valor Real (Uvr)
Solución: Se calcula
-La tasa efectiva anual cuando interviene la corrección monetaria:
i = (1 + ic) (1 + i e) – 1
i = (1 + 0,08) (1 + 0,13) – 1
i = 0,2204
Ahora se halla la tasa efectiva mensual a partir de la expresión:
i = (1 + i sp) m – 1
0,22 = (1 + i m) 12 – 1
1,22 = (1 + i m) 12
1,22 1/12 = 1 + i m
1,01670896 – 1 = i m
i m = 0,01670896
Del enunciado se obtiene: A = 1.000.000 y n = 60 meses
Reemplazando en R = A (i sp ) / [1 – (1 + i sp ) – n] se tiene:
R = 1.000.000 (0,01670896) / [1 – (1 + 0,01670896) – 60]
R = 16.708,96387 / 0,630
R = 26.522,16487
Rta: El valor de la cuota es $26.522,16
Para elaborar la tabla de amortización se realizan los siguientes pasos:
1.
2.
Primer registro: n = 0, el saldo de la deuda en pesos es $1.000.000
Segundo registro: n = 1, la primera cuota es $26.522,16
El interés se obtiene multiplicando el saldo inmediatamente anterior de la
deuda por la tasa de interés mensual así: $1.000.000 x 0,01670896 = 16.708,96
La amortización se obtiene al restarle a la cuota el interés:26.522,16 – 16.708,96
= 9.813,20
El nuevo saldo es la diferencia entre el saldo anterior y la amortización:
1.000.000 – 9.813,2 = 990.186,80
3.
Para cada una de los registros siguientes se realiza el mismo procedimiento del paso 2.
Ernesto Vélez Betancur
Jorge Ernesto Pérez Hernández
Porik aN
271
Tabla 2.2.1. Cuota constante en pesos.
n
CUOTA
INTERES
AMORTIZACION
SALDO
0
1.000.000
1
26.522,16
16.708,96
9.813,20
990.186,80
2
26.522,16
16.544,99
9.977,17
980.209,63
3
26.522,16
16.378,28
10.143,88
970.065,75
4
26.522,16
16.208,78
10.313,38
959.752,37
…
(Fuente: Circular externa 068 del 13 de septiembre de 2000 de la antigua Superintendencia Bancaria)
2.2.2. Amortización Constante a Capital
Las cuotas mensuales son iguales a la enésima parte de la deuda más los intereses del mes calculados sobre el saldo insoluto. De esta forma, las cuotas
mensuales en pesos son decrecientes.
Ct = D / n + ( isp . St-1)
Donde:
Ct = Cuota en pesos a la altura t, t=1,2,3.....n
D = Valor de la deuda en pesos
St-1 = saldo a la altura t-1 , St-1 = D – [( t – 1 )( D* / n )]
isp = tasa efectiva mensual equivalente = ((1+ia) (1/12))-1, ia tasa efectiva anual
sobre pesos que no podrá incrementarse durante el plazo.
n = Número de meses del plazo
D* = Saldo de la deuda en pesos en el momento t-1
Ejemplo. A partir de la información dada en el ejemplo para el Sistema de
la Cuota Constante en pesos, determinar el valor de las cuotas y elaborar la
respectiva tabla.
Solución: Se calcula:
-La tasa efectiva anual cuando interviene la corrección monetaria:
i = (1 + ic) (1 + i e) – 1
i = (1 + 0,08) (1 + 0,13) – 1
i = 0,2204
Ahora se halla la tasa efectiva mensual a partir de la expresión:
i = (1 + i sp) m – 1
272
Porik aN
Sistema en Unidades de Valor Real (Uvr)
0,22 = (1 + i m) 12 – 1
1,22 = (1 + i m) 12
1,22 1/12 = 1 + i m
1,01670896 – 1 = i m
i m = 0,01670896
Se calcula el saldo en el momento t – 1 mediante la expresión:
St-1 = D – [(t – 1)(D* / n)]
Como es en el primer momento, entonces:
St–1 = 1.000.000 – [(1 – 1)( 1.000.000/60)]
St–1 = 1.000.000
Reemplazando en Ct = D / n + ( isp . St-1), se tiene:
Ctu = 1.000.000 / 60 + (1.000.000 x 0,01670896)
Ctu = 16.666,6666 + 16.708,96
Ctu= 33.375,6266
Rta: El valor de la cuota es de $33.375,62
Para elaborar la tabla de amortización se realizan los siguientes pasos:
1.
2.
Primer registro: n = 0, el saldo de la deuda en pesos es $1.000.000
Segundo registro: n = 1, la cuota es $33.375,62
El interés se obtiene multiplicando el saldo inmediatamente anterior de la
deuda por la tasa de interés mensual así: 1.000.000 x 0,01670896 = 16.708,96
La amortización como es constante, se obtiene al dividir el total de la deuda
en pesos entre el número de periodos en que se va a cancelar:
1.000.000 / 60 = 16.666,6666 = 16.666,6666
El nuevo saldo es la diferencia entre el saldo anterior y la amortización:
1.000.000 – 16.666,6666 = 983.333,3333
3.
Tercer registro: n = 2.
D = 1.000.0000, i sp=0,01670896, n=59, D* = 983.333,3333, St–1 =?, Cuota 2: ?
St-1 = 1.000.000 – (2 – 1)(983.333,3333 / 59)
St-1 = 1.000.000 – (1)(16.666,6666)
St–1= 1.000.000 – 16.666,6666 = 983.333,3333
Ernesto Vélez Betancur
Jorge Ernesto Pérez Hernández
Porik aN
273
El valor de la cuota se halla con Ct = D / n + ( isp . St-1)
Ct = 1.000.0000 / 60 + ( 983.333,3333 x 0,01670896)
Ct = 16.666,6666 + 16.430,47733
Ct = 33.097,14
Para el valor de los intereses, la amortización y el nuevo saldo se procede igual
que en el paso 2.
4.
Para cada una de los registros siguientes se realiza el mismo procedimiento del paso 3.
Tabla 2.2.2. Amortización constante en pesos.
n
CUOTA
0
1
33.375,62
2
33.097,14
3
32.818,65
4
32.540,17
…
(Fuente: Circular externa
INTERES
AMORTIZACION
16.708,96
16.430,47
16.151,99
15.873,51
16.666,6666
16.666,6666
16.666,6666
16.666,6666
SALDO
1.000.000
983.333,3333
966.666,6666
950.000
8.382,9876
068 del 13 de septiembre de 2000 de la antigua Superin-
tendencia Bancaria)
3. Conclusion
No se podrá capitalizar intereses en los créditos de vivienda a largo plazo tal
como lo estipula la ley 546 del 23 de diciembre de 1999 en razón a que expresamente se establece que se debe tener una tasa de interés remuneratoria,
calculada sobre las UVR la cual se cobrará en forma vencida y no podrá capitalizarse y que los sistemas de amortización que se aprueben no contemplaran
capitalización de intereses. No obstante, al materializarse la aprobación de
los sistemas de amortización por parte de la Superintendencia Bancaria en
las circulares externas 068 del 13 de septiembre de 2000 y 085 del 29 de diciembre del mismo año, en las que expresamente se retoma lo que dice la Ley
inmediatamente anterior en relación con los intereses, estos sistemas permiten
la capitalización de intereses, tal como se demuestra en el desarrollo de los
ejemplos objeto de este documento donde las fórmulas utilizadas tienen la
estructura matemática del Interés Compuesto, cuyo elemento esencial es la
capitalización de intereses. Lo anterior ha determinado que desde la misma
274
Porik aN
Sistema en Unidades de Valor Real (Uvr)
aprobación de la ley marco de vivienda y la posterior puesta en vigencia de las
disposiciones que reglamentan por parte del organismo de vigilancia y control
los parámetros de aplicación de la aludida ley, se hayan presentado demandas
que han buscado poner en conocimiento de las autoridades judiciales este
detrimento patrimonial. No obstante lo anterior, aún persiste la aplicación
del sistema de capitalización de intereses, lo cuál constituye una situación en
extremo incongruente, si se parte de la base de que precisamente la ley 546 y
la Superintendencia Financiera lo prohíben.
Ernesto Vélez Betancur
Jorge Ernesto Pérez Hernández
Porik aN
275
Anexos
Anexo 1.
Evolución de la Formula de Calculo de la Corrección Monetaria
FECHA
NORMA
17-07-72
DEC 1229
PROMEDIO IPC, CORRESPONDIENTE AL TRIMESTRE
INMEDIATAMENTE ANTERIOR
05-24-73
DEC 969
PROMEDIO IPC CORRESPONDIENTE A LOS DOCE
MESES INMEDIATAMENTE ANTERIORES
20-02-74
DEC-269
PROMEDIO IPC CORRESPONDIENTE A LOS 24 MESES
ANTERIORES.
12-08-74
DEC 1728
PROMEDIO IPC CORRESPONDIENTE A LOS 24 MESES
INMEDIATAMENTE ANTERIORES CON LIMITE AL
AUMENTO DE SU VALOR DEL 20% ANUAL
21-08-75
DEC 1685
PROMEDIO IPC CORRESPONDIENTE A LOS 24 MESES
INMEDIATAMENTE ANTERIORES CON LIMITE AL
AUMENTO DE SU VALOR DEL 19% ANUAL
15-01-76
DEC 58
IPC ANUAL CORRESPONDIENTE A LOS DOCE MESES
INMEDIATAMENTE ANTERIORES, CON LIMITE AL
AUMENTO DE SU VALOR DEL 18% ANUAL
27-03-79
DEC 664
IPC ANUAL, CORRESPONDIENTE A LOS DOCE MESES
INMEDIATAMENTE ANTERIORES, CON LIMITE AL
AUMENTO DE SU VALOR DEL 19%
17-09-80
DEC 2475
IPC ANUAL, CORRESPONDIENTE A LOS DOCE MESES
INMEDIATAMENTE ANTERIORES CON LIMITE AL
AUMENTO DE SU VALOR DEL 21% ANUAL
11-10-82
DEC 2929
IPC ANUAL CORRESPONDIENTE A LOS DOCE MESES
INMEDIATAMENTE ANTERIORES CON LIMITE AL
AUMENTO DE SU VALOR DEL 23% ANUAL
16-05-84
DEC 1131
IPC EMPLEADO Y OBREROS. 12 MESES ANTERIORES
MAS 0.015 ( IPC – TASA CDT BANCOS Y CORP. FINAN) ^ 2
24-01-86
DEC 272
LIMITA EL AUMENTO DE SU VALOR AL 21% ANUAL,
SIGUE CALCULO DEL DEC 1131/84
25-03-88
DEC 530
LIMITA EL AUMENTO DE SU VALOR AL 22% ANUAL,
SIGUE CALCULO DEL DEC 1131/84
DEC 1319
40% IPC ANUAL, CORRESPONDIENTE A LOS 12 MESES
INMEDIATAMENTE ANTERIORES, MAS 35% DEL
PROMEDIO DEL A DTF CORRESPONDIENTE AL MES
INMEDIATAMENTE ANTERIOR, CON LIMITE AL AUMENTO
DE SU VALOR DEL 24% ANUAL.
07-07-88
TOPES Y FORMULAS DE LA CORRECCIÓN MONETARIA
276
Porik aN
Sistema en Unidades de Valor Real (Uvr)
DEC 1127
45% IPC ANUAL, CORRESPONDIENTE ALOS 12 MESES
INMEDIATAMENTE ANTERIORES, MAS 35% DEL
PROMEDIO DE LA DTF CORRESPONDIENTE AL MES
INMEDIATAMENTE ANTERIOR, SE ELIMINO EL TOPE
MAXIMO.
21-04-92
DEC 678
20% IPC ANUAL, CORRESPONDIENTE A LOS MESES
12 INMEDIATAMENTE ANTERIORES MAS 50% DEL
PROMEDIO DELA DTF CORRESPONDIENTES A LAS
OCHO SEMANAS INMEDIATAMENTE ANTERIORES A LA
FECHA DEL CALCULO.
15-03-93
RES.06
90% DEL COSTO PROMEDIO PONDERADO DE LAS
CAPTACIONES EN CUENTAS DE AHORRO DE VALOR
CONSTANTE Y CDT DEL MES CALENDARIO ANTERIOR
AL CÁLCULO.
15-04-93
RES.10
90% DEL COSTO DEL PROMEDIO PONDERADO DE LAS
CAPTACIONES EN CUENTAS DE AHORRO DE VALOR
CONSTANTE Y CDT DEL MES CALENDARIO ANTERIOR
AL CALCULO O UNA TASA EFECTIVA ANUAL AL 19%. SE
TOMARA LA QUE RESULTE MAYOR.
09-09-94
RES. 26
74% DEL PROMEDIO MOVIL DE LA DTF DE LAS 12
SEMANAS ANTERIORES A LA FECHA DEL CÁLCULO.
30-06-95
RES. 18
74% DEL PROMEDIO MOVIL DE LA DTF DE LAS 4
SEMANAS ANTERIORES A LA FECHA DE CÁLCULO.
05-03-99
RES. 6
74% DEL PROMEDIO PONDERADO DE LA DTF
EFECTIVA DE LAS CUATRO (4) SEMANAS ANTERIORES
A ESTA, PONDERARAN UN 30%, 20%, Y 10%
RESPECTIVAMENTE.
29-05-90
14-05-99
01-06-99
RES. EXT. 8
RES. EXT. 10
Fuente: Banco de la República.
PORCENTAJE VARIBLE DE LA TASA DE INTERES
DE MERCADO, DEFINIDA ESTA ÚLTIMA EN LA
MISMA FORMA EN QUE VENIA DEFINIENDOSE.
EL PORCENTAJE MENCIONADO SERA DEFINIDO
MENSUALMENTE POR LA RELACION ENTRE EL
PROMEDIO DE LAS TASAS ANUALES DE INFLACION DEL
IPC OBSERVADAS EN LOS DOCE MESES ANTERIORES
(pi) Y LAS TASAS DE INTERES REAL DE LARGO PLAZO
(rL), SE CALCULARA UTILIZANDO EL PROMEDIO DE LA
DTF, DEFLACTADA POR INFLACION DEL IPC, DESDE
ENERO DE 1988 HASTA EL MES ANTERIOR A AQUEL EN
EL CUAL SE HACE EL CALCULO.
SE ATA LA CORRECCION MONETARIA A LA INFLACION,
DEFINIDA POR EL PROMEDIO DE LAS TASAS DE
INFLACION DE LOS 12 MESES ANTERIORES A AQUEL
EN QUE SE CALCULA. SE ESTABLECE UNA TRANSICION
DE 6 MESES EN QUE SE INCREMENTA GRADUALMENTE
LA PROPORCION DE LA INFLACION QUE SE TIENE
EN CUENTA, HASTA LLEGAR EN DICIEMBRE DE 1999
A UNA FORMULA QUE IGUALA LA INFLACION Y LA
CORRECCION. LA PONDERACION ES: JUNIO 99: 79.72%,
JULIO 99. 83%, AGOS 99: 86%, SEPT 99: 90%, OCT 99:
93%, NOVI 99: 97% Y DIC 99: 100%.
Ernesto Vélez Betancur
Jorge Ernesto Pérez Hernández
Porik aN
277
Referencias
ARANGO LONDOÑO, Gilberto, (1993), Estructura Económica Colombiana,
Bogotá: Universidad Javeriana Publicaciones, Séptima Edición.
BANCO DE LA REPUBLICA (1972). Dcto 1229 del 17 de julio de 1972.
BANCO DE LA REPUBLICA (1973). Dcto 969 del 24 de mayo de 1973.
BANCO DE LA REPUBLICA (1974). Dcto 269 del 20 de febrero de 1974.
BANCO DE LA REPUBLICA (1974). Dcto 1728 del 12 de agosto de 1972.
BANCO DE LA REPUBLICA (1975). Dcto 1685 del 21 de agosto de 1975.
BANCO DE LA REPUBLICA (1976). Dcto 58 del 15 de enero de 1976.
BANCO DE LA REPUBLICA (1979). Dcto 664 del 25 de marzo de 1979.
BANCO DE LA REPUBLICA (1980). Dcto 2475 del 17 de septiembre de 1980.
BANCO DE LA REPUBLICA (1982). Dcto 2929 del 11 de octubre de 1982.
BANCO DE LA REPUBLICA (1984). Dcto 1131 del 16 de mayo de 1984.
BANCO DE LA REPUBLICA (1986). Dcto 272 del 24 de enero de 1986.
BANCO DE LA REPUBLICA (1988). Dcto 530 del 25de marzo de 1988.
BANCO DE LA REPUBLICA (1988). Dcto 1319 del 7 de julio de 1988.
BANCO DE LA REPUBLICA (1990). Dcto 1127 del 29 de mayo de 1990.
BANCO DE LA REPUBLICA (1992). Dcto 678 del 21 de abril de 1992.
BANCO DE LA REPUBLICA (1993). Res. 06 del 15 de marzo de 1993.
BANCO DE LA REPUBLICA (1993). Res. 10 del 15 de abril de 1993.
BANCO DE LA REPUBLICA (1994). Res. 26 del 09 de septiembre de 1994.
BANCO DE LA REPUBLICA (1995). Res. 18 del 30 de junio de 1995.
BANCO DE LA REPUBLICA (1999). Res. 06 del 05 de marzo de 1999.
BANCO DE LA REPUBLICA (1999). Res. Ext. 08 del 14 de mayo de 1999.
BANCO DE LA REPUBLICA (1999). Res. Ext. 10 del 01 de junio de 1999.
BANCO DE LA REPUBLICA (2000). Res. Ext. 13 del 11 de agosto de 2000.
CONGRESO DE LA REPUBLICA (1999). Ley Marco 546 del 23 de diciembre de 1999.
CONSEJO DE ESTADO (1999). Sentencia 9280 del 21 de mayo de 1999
CORTE CONSTITUCIONAL (1999). Sentencia C – 383 del 27 de mayo
de 1999
CORTE CONSTITUCIONAL (1999). Sentencia C – 700 del 16 de septiembre de 1999.
CORTE CONSTITUCIONAL (1999). Sentencia C – 747 del 6 de octubre
de 1999.
CURRIE, Lauchlin, (1968), Desarrollo Económico Acelerado, México FCE.
PASCHOAL ROSSETTI, José, (2004), Introducción a la Economía, Mèxico:
Alfaomega,
278
Porik aN
Sistema en Unidades de Valor Real (Uvr)
Tercera Edición.
SUPERINTENDENCIA BANCARIA (2000). Circular Externa No 068 del
13 de septiembre de 2000.
SUPERINTENDENCIA BANCARIA ( 2000). Circular Externa No 085 del
29 de diciembre de 2000.