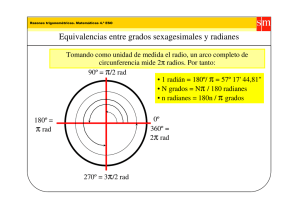
SISTEMA DE MEDIDAS ANGULARES DEFINICIÓN Son las formas como se pueden medir los ángulos, entre los cuales destacan los siguientes: Sistema Unidad ∡ 1 vuelta Sexagesimal 1° 360° Centesimal 1 400 g Radial o circular 1 rad g FÓRMULA GENERAL DE CONVERSIÓN Es aquella relación entre los números que representan la medida de un ángulo en los tres sistemas conocidos. Esto es, dado el ángulo , se cumple que: 2 rad Subunidades Sexagesimal Centesimal 1° = 60’ 1g = 100m 1’ = 60’’ 1m = 100s 1° = 3600’’ 1g = 10000s Observación 𝐶 𝑅 𝑆 = = 180 200 𝜋 S° Cg R rad De donde se pueden sacar las siguientes conclusiones: 1. 𝑆 180 = 𝐶 200 2. 𝑆 180 = 𝑅 𝜋 𝑆 = 180 𝑅 𝜋 𝑅 𝐶 = 200 𝑅 3. 𝐶 200 = 𝜋 𝑆 9 = 𝐶 10 𝜋 1. 1 rad > 1° > 1g 2. 180° < > 200g < > rad 3. 9° < > 10g EJERCICIOS: 1. Calcular 𝐸 = 4. 27’ < > 50m 81’’ < > 250s 5° 30′ 10′ 5. 𝛼 = 𝑎° 𝑏 ′ 𝑐 ′′ = 𝑎° + 𝑏 ′ + 𝑐′′ 6. 𝛽 = 𝑥 𝑔 𝑦 𝑚 𝑧 𝑠 = 𝑥 𝑔 + 𝑦 𝑚 + 𝑧 𝑠 CONVERSIÓN ENTRE SISTEMAS Es el procedimiento mediante el cual un ángulo expresado en cierto sistema se expresa en otro sistema; es decir, en otras unidades. El procedimiento se denomina “factor de conversión” y su uso se muestra en los siguientes ejemplos: 2. Convertir 10° a radianes 1. Exprese 60° en radianes. 3. Convertir 2. Exprese 40g en grados sexagesimales. 𝜋 9 3. Exprese rad en grados sexagesimales. 𝜋 18 rad a grados sexagesimales. 4. Calcular: 𝐻 = 𝜋 𝑟𝑎𝑑+10° 2 20° 5. Siendo S y C lo conocido para un ángulo no nulo, ¿a qué es igual E? 𝐶+𝑆 𝐸 = 𝐶−𝑆 6. Siendo S y C lo conocido para un ángulo no nulo, reducir: 2𝑆 − 𝐶 𝐾=√ 𝐶−𝑆 8. Calcular “x”, si: (7𝑥 − 4)° = 𝜋 4 𝑟𝑎𝑑 9. Siendo S y C, lo conocido para un mismo ángulo. Calcule la medida centesimal si se cumple: 1 1 + 𝑆 𝐶 =2 1 𝑆𝐶 10. Señale la medida radial de un ángulo que cumple: 𝑆 2 𝐶 2 20𝑅 2 + + =𝑆+𝐶+𝑅 𝜋 9 10 11. Si R representa la medida de un ángulo en radianes, además: 𝜋 𝑅 2√ − 3√ = 2√2 𝑅 𝜋 7. Calcular: 𝑀= 𝜋 𝑟𝑎𝑑+14° 5 10° Halla la medida de dicho ángulo en grados sexagesimales.