Teoremas de Thevenin y de Norton en circuitos de corriente alterna
Anuncio

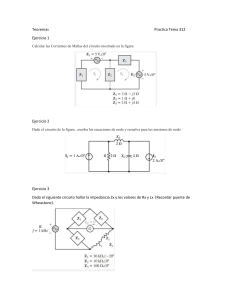
Teoremas de Thevenin y de Norton en circuitos de corriente alterna Estos teoremas nos ayudan a simplificar circuitos. En la práctica sucede que el valor de un elemento de circuito es variable (usualmente llamado carga), mientras que el resto de elementos del circuito tienen valores fijos. En el caso de que la carga cambie de valor, para determinar datos eléctricos del circuito hacia la carga, el circuito completo deberá analizarse de nuevo. Para evitar este proceso largo, estos teoremas proporcionan una técnica para reemplazar el circuito de valores fijos por uno equivalente simple. Teorema de Thevenin De acuerdo a este teorema, cualquier circuito lineal complejo se puede reeplazar por un circuito simple de una sola fuente de tensión con una impedancia en serie, llamado CIRCUITO EQUIVALENTE DE THEVENIN, dónde la tensión entre las terminales a y b a circuito abierto es la tensión de la fuente de Thevenin. como se observa en el circuito siguiente: Teorema de Norton El teorema de Norton establece que un circuito lineal de dos terminales puede reemplazarse por un circuito equivalente, que consta de una fuente de corriente I N en paralelo con una impedancia ZN, llamado CIRCUITO EQUIVALENTE DE NORTON, dónde la corriente de cortocircuito a través de las terminales a y b es la corriente de la fuente de Norton. Como se muestra en el circuito siguiente: En ambos casos ZTh y ZN se calculan de la misma forma, por lo que ya se sabe sobre la transformación de fuentes, la impedancia de Thévenin y de Norton son iguales. Para aclarar el procedimiento para obtener los circuitos equivalentes de Thevenin y de Norton, realizaremos algunos ejemplos. MACR Dado el circuito siguiente, determinar los circuitos equivalentes de Thevenin y de Norton, para calcular VX de la carga conectada: Se identifica la carga en el circuito: Para ambos teoremas, se desconecta la carga y se pueden marcar las terminales como a y b: Ahora se determina la impedancia de Thevenin, que es el mismo procedimiento para calcular la impedancia de Norton, es decir ZTH = ZN, donde todas las fuentes del circuito se llevan a cero, reemplazando las fuentes de tensión por un corto circuito y las fuentes de corriente por un circuito abierto: MACR Se identifican las conexiones de todas las impedancias del circuito para reducir hacia las terminales a y b: Las impedancias conectadas en serie: 𝑍𝑅1 , 𝑍𝑅2 𝑦 𝑍𝐶1 están 𝒁𝑨 = 𝒁𝑹𝟏 + 𝒁𝑹𝟐 + 𝒁𝑪𝟏 𝒁𝑨 = 𝟏𝟐 + 𝟒 − 𝒋𝟏𝟔 𝐤𝛀 𝒁𝑨 = 𝟏𝟔 − 𝒋𝟏𝟔 𝒌𝛀 = 𝟐𝟐. 𝟔𝟑∠ − 𝟒𝟓° 𝐤𝛀 La impedancia 𝒁𝑨 está en paralelo con la impedancia 𝒁𝑪𝟐 : 𝒁𝑩 = 𝒁𝑨 𝒁𝑪𝟐 (𝟏𝟔 − 𝒋𝟏𝟔)(−𝒋𝟏𝟎) = 𝒁𝑨 + 𝒁𝑩 𝟏𝟔 − 𝒋𝟏𝟔 − 𝒋𝟏𝟎 𝒁𝑩 = 𝟏. 𝟕𝟐 − 𝒋𝟕. 𝟐𝟏 𝒌𝛀 = 𝟕. 𝟒𝟏∠ − 𝟕𝟔. 𝟓𝟖° 𝐤𝛀 Finalmente, 𝒁𝑩 está en serie con 𝒁𝑹𝟑 : 𝒁𝑻𝒉 = 𝒁𝑵 = 𝒁𝑩 + 𝒁𝑹𝟑 = 𝟏. 𝟕𝟐 − 𝒋𝟕. 𝟐𝟏 + 𝟑 𝒁𝑻𝒉 = 𝒁𝑵 = 𝟒. 𝟕𝟐 − 𝒋𝟕. 𝟐𝟏 𝒌𝛀 = 𝟖. 𝟔𝟐∠ − 𝟓𝟔. 𝟕𝟗° 𝐤𝛀 Se obtendrán los valores 𝑉𝑇ℎ y 𝐼𝑁 en forma paralela para comprobar el resultado 𝑉𝑋 con ambos teoremas: Thevenin Norton Se restablecen las fuentes a sus valores originales y se calcula la tensión a circuito abierto entre las terminales a y b: Se restablecen las fuentes a sus valores originales y se calcula la corriente de corto circuito a través de las terminales a y b: MACR La tensión en el resistor 𝑍𝑅3 es cero, al quedar Resolviendo por el método de mallas: el circuito abierto en la carga, por lo tanto, se puede determinar 𝑉𝑇ℎ , cómo se observa en la Malla I1: imagen siguiente: 𝑰𝟏 = 𝟏∠𝟎° 𝒎𝑨 Malla I2: −𝒋𝟏𝟔𝟎𝟎𝟎(𝑰𝟐 − 𝑰𝟏 ) + 𝟏𝟐𝟎𝟎𝟎(𝑰𝟐 − 𝑰𝟏 ) + 𝟒𝟎𝟎𝟎𝑰𝟐 − 𝒋𝟏𝟎𝟎𝟎𝟎(𝑰𝟐 − 𝑰𝟑 ) + 𝟑𝟎∠𝟑𝟎° = 𝟎 (−𝟏𝟐𝟎𝟎𝟎 + 𝒋𝟏𝟔𝟎𝟎𝟎)𝑰𝟏 + (𝟏𝟔𝟎𝟎𝟎 − 𝒋𝟐𝟔𝟎𝟎𝟎)𝑰𝟐 + 𝒋𝟏𝟎𝟎𝟎𝟎𝑰𝟑 = −𝟑𝟎∠𝟑𝟎° Sustituyendo I1=10° mA (−𝟏𝟐𝟎𝟎𝟎 + 𝒋𝟏𝟔𝟎𝟎𝟎)(𝟎. 𝟎𝟎𝟏) + (𝟏𝟔𝟎𝟎𝟎 − 𝒋𝟐𝟔𝟎𝟎𝟎)𝑰𝟐 + 𝒋𝟏𝟎𝟎𝟎𝟎𝑰𝟑 = −𝟑𝟎∠𝟑𝟎° −𝟏𝟐 + 𝒋𝟏𝟔 + (𝟏𝟔𝟎𝟎𝟎 − 𝒋𝟐𝟔𝟎𝟎𝟎)𝑰𝟐 + 𝒋𝟏𝟎𝟎𝟎𝟎𝑰𝟑 = −𝟑𝟎∠𝟑𝟎° (𝟏𝟔𝟎𝟎𝟎 − 𝒋𝟐𝟔𝟎𝟎𝟎)𝑰𝟐 + 𝒋𝟏𝟎𝟎𝟎𝟎𝑰𝟑 = −(𝟐𝟓. 𝟗𝟖 + 𝒋𝟏𝟓) + 𝟏𝟐 − 𝒋𝟏𝟔 (𝟏𝟔𝟎𝟎𝟎 − 𝒋𝟐𝟔𝟎𝟎𝟎)𝑰𝟐 + 𝒋𝟏𝟎𝟎𝟎𝟎𝑰𝟑 = −𝟏𝟑. 𝟗𝟖 − 𝒋𝟑𝟏 Resolviendo por el método de nodos: (𝟏𝟔𝟎𝟎𝟎 − 𝒋𝟐𝟔𝟎𝟎𝟎)𝑰𝟐 + 𝒋𝟏𝟎𝟎𝟎𝟎𝑰𝟑 = 𝟑𝟒∠ − 𝟏𝟏𝟒. 𝟐𝟕° ⟹ (𝑨) Nodo V1: Malla I3: 𝑽𝟏 − 𝑽𝑻𝒉 𝑽𝟏 − 𝑽𝟎 + = 𝟎. 𝟎𝟎𝟏∠𝟎° 𝟒𝟎𝟎𝟎 𝟏𝟐𝟎𝟎𝟎 − 𝒋𝟏𝟔𝟎𝟎𝟎 −𝒋𝟏𝟎𝟎𝟎𝟎(𝑰𝟑 − 𝑰𝟐 ) + 𝟑𝟎𝟎𝟎𝑰𝟑 − 𝟑𝟎∠𝟑𝟎° = 𝟎 𝑽𝟏 𝑽𝑻𝒉 𝑽𝟏 − + = 𝟎. 𝟎𝟎𝟏∠𝟎° 𝟒𝟎𝟎𝟎 𝟒𝟎𝟎𝟎 𝟏𝟐𝟎𝟎𝟎 − 𝒋𝟏𝟔𝟎𝟎𝟎 𝒋𝟏𝟎𝟎𝟎𝟎𝑰𝟐 + (𝟑𝟎𝟎𝟎 − 𝒋𝟏𝟎𝟎𝟎𝟎)𝑰𝟑 = 𝟑𝟎∠𝟑𝟎° ⟹ (𝑩) 𝑽𝟏 𝑽𝑻𝒉 (𝟏𝟐𝟎𝟎𝟎 + 𝒋𝟏𝟔𝟎𝟎𝟎) − + 𝑽𝟏 = 𝟎. 𝟎𝟎𝟏∠𝟎° 𝟒𝟎𝟎𝟎 𝟒𝟎𝟎𝟎 𝟒𝟎𝟎𝟎𝟎𝟎𝟎𝟎𝟎 𝑽𝟏 𝑽𝑻𝒉 𝟑 𝟏 ( − + 𝑽 +𝒋 𝑽 = 𝟎. 𝟎𝟎𝟏∠𝟎°) 𝒙𝟏𝟎𝟎𝟎𝟎𝟎 𝟒𝟎𝟎𝟎 𝟒𝟎𝟎𝟎 𝟏𝟎𝟎𝟎𝟎𝟎 𝟏 𝟐𝟓𝟎𝟎𝟎 𝟏 Expresando las ecuaciones matrices: (A) y (B) en 𝟏𝟔𝟎𝟎𝟎 − 𝒋𝟐𝟔𝟎𝟎𝟎 𝒋𝟏𝟎𝟎𝟎𝟎 𝑰 𝟑𝟒∠ − 𝟏𝟏𝟒. 𝟐𝟕° [ ] [ 𝟐] = [ ] 𝒋𝟏𝟎𝟎𝟎𝟎 𝟑𝟎𝟎𝟎 − 𝒋𝟏𝟎𝟎𝟎𝟎 𝑰𝟑 𝟑𝟎∠𝟑𝟎° 𝑰𝟐 = 𝟏. 𝟏𝟐∠ − 𝟏𝟖. 𝟐𝟔° 𝒎𝑨 𝟐𝟓𝑽𝟏 − 𝟐𝟓𝑽𝑻𝒉 + 𝟑𝑽𝟏 + 𝒋𝟒𝑽𝟏 = 𝟏𝟎𝟎∠𝟎° 𝑰𝟑 = 𝑰𝑵 = 𝟐. 𝟐∠𝟖𝟒. 𝟑𝟖° 𝒎𝑨 (𝟐𝟖 + 𝒋𝟒)𝑽𝟏 − 𝟐𝟓𝑽𝑻𝒉 = 𝟏𝟎𝟎∠𝟎° ⟹ (𝟏) Por lo tanto, el circuito de Norton queda: Nodo VTh: 𝑽𝑻𝒉 − 𝑽𝟏 𝑽𝑻𝒉 − 𝟑𝟎∠𝟑𝟎° + =𝟎 𝟒𝟎𝟎𝟎 −𝒋𝟏𝟎𝟎𝟎𝟎 𝑽𝑻𝒉 − 𝑽𝟏 𝑽𝑻𝒉 − (𝟐𝟓. 𝟗𝟖 + 𝒋𝟏𝟓) + =𝟎 𝟒𝟎𝟎𝟎 −𝒋𝟏𝟎𝟎𝟎𝟎 𝑽𝑻𝒉 𝑽𝟏 𝑽𝑻𝒉 (𝟐𝟓. 𝟗𝟖 + 𝒋𝟏𝟓) − + + =𝟎 𝟒𝟎𝟎𝟎 𝟒𝟎𝟎𝟎 −𝒋𝟏𝟎𝟎𝟎𝟎 𝒋𝟏𝟎𝟎𝟎𝟎 ( Conectando la carga nuevamente, determina VX por la ley de Ohm: 𝑽𝑻𝒉 𝑽𝟏 𝑽𝑻𝒉 𝟐𝟓. 𝟗𝟖 𝟏𝟓 − +𝒋 −𝒋 + = 𝟎) 𝒙𝟐𝟎𝟎𝟎𝟎 𝟒𝟎𝟎𝟎 𝟒𝟎𝟎𝟎 𝟏𝟎𝟎𝟎𝟎 𝟏𝟎𝟎𝟎𝟎 𝟏𝟎𝟎𝟎𝟎 se 𝟓𝑽𝑻𝒉 − 𝟓𝑽𝟏 + 𝒋𝟐𝑽𝑻𝒉 − 𝒋𝟓𝟏. 𝟗𝟔 + 𝟑𝟎 = 𝟎 −𝟓𝑽𝟏 + (𝟓 + 𝒋𝟐)𝑽𝑻𝒉 = −𝟑𝟎 + 𝒋𝟓𝟏. 𝟗𝟔 −𝟓𝑽𝟏 +(𝟓 + 𝒋𝟐)𝑽𝑻𝒉 = 𝟔𝟎∠𝟏𝟐𝟎° ⟹ (𝟐) Expresando las ecuaciones (1) y (2) matrices: 𝟐𝟖 + 𝒋𝟒 −𝟐𝟓 𝑽 𝟏𝟎𝟎∠𝟎° [ ][ 𝟏 ] = [ ] −𝟓 𝟓 + 𝒋𝟐 𝑽𝑻𝒉 𝟔𝟎∠𝟏𝟐𝟎° en 𝑽𝑿 = 𝑰𝑵 𝒁𝑻 = (𝟐. 𝟐𝒙𝟏𝟎−𝟑∠𝟖𝟒. 𝟑𝟖°) ( (𝟒𝟕𝟐𝟎 − 𝒋𝟕𝟐𝟏𝟎)(𝒋𝟗𝟎𝟎𝟎) ) 𝟒𝟕𝟐𝟎 − 𝒋𝟕𝟐𝟏𝟎 + 𝒋𝟗𝟎𝟎𝟎 𝑽𝑿 = 𝟑𝟑. 𝟕𝟑∠𝟗𝟔. 𝟖𝟐° 𝑽 MACR La solución es: 𝑽𝟏 = 𝟏𝟗. 𝟐𝟔 + 𝒋𝟓. 𝟎𝟔 𝑽 = 𝟏𝟗. 𝟗𝟏∠𝟏𝟒. 𝟕𝟑° 𝑽 𝑽𝑻𝒉 = 𝟏𝟔. 𝟕𝟔 + 𝒋𝟖. 𝟕𝟓 𝑽 = 𝟏𝟖. 𝟗𝟏∠𝟐𝟕. 𝟓𝟖° 𝑽 Por lo tanto, el circuito de Thevenin queda: Conectando la carga nuevamente, determina VX por divisor de tensión: 𝑽𝑿 = se 𝒁𝑳 𝒋𝟗𝟎𝟎𝟎 (𝟏𝟖. 𝟗𝟏∠𝟐𝟕. 𝟓𝟖°) 𝑽𝑻𝒉 = 𝒁𝑻 𝟒𝟕𝟐𝟎 − 𝒋𝟕𝟐𝟏𝟎 + 𝒋𝟗𝟎𝟎𝟎 𝑽𝑿 = 𝟑𝟑. 𝟕𝟏∠𝟗𝟔. 𝟖𝟏° 𝑽 MACR