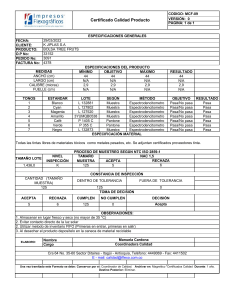
TIPO FORMULA PROCEDIMIENTO CONDICIÓN 𝑘 Bondad de ajuste 𝑥𝑖 − 𝑛𝑝𝑖 𝑛𝑝𝑖 𝑤= 2 𝜑 =𝑘−1−𝑚 𝜑: Grados de libertad 𝑖=1 Independencia CHI CUADRADO Homogeneidad 𝑡𝑜𝑡𝑎𝑙 𝑓𝑖𝑙𝑎 𝑥 𝑡𝑜𝑡𝑎𝑙 𝑐𝑜𝑙𝑢𝑚𝑛𝑎 𝐹𝑟𝑒𝑐𝑢𝑒𝑛𝑐𝑖𝑎 𝑒𝑠𝑝𝑒𝑟𝑎𝑑𝑎 = 𝑛𝑝 = 𝑔𝑟𝑎𝑛 𝑡𝑜𝑡𝑎𝑙 2 𝑋𝑐𝑎𝑙 = 𝑜𝑖 − 𝑒𝑖 𝑒𝑖 2 1. Hipótesis 2. Nivel de significación 3. Estadística 4. Región crítica 5. Cálculos 6. Desición 2 2 𝑆𝑖 𝜒𝑐𝑎𝑙 > 𝑋1−𝛼,𝜑 𝑒𝑛𝑡𝑜𝑛𝑐𝑒𝑠 𝐻0 𝑠𝑒 𝑟𝑒𝑐ℎ𝑎𝑧𝑎 𝑖 𝑝𝑖ҧ ∓ 𝑧1−𝛼 2 Igualdad de proporciones Se compara nmas 𝑧1−𝛼 𝑝𝑖ҧ 1 − 𝑝𝑖 + 𝑝ഥ𝑗 1 − 𝑝𝑗ҧ − 2𝑝ഥ𝑖 𝑝ഥ𝑗 2 𝑝ҧ𝑖 − 𝑝𝑗ҧ ∓ Prueba de signos Wilcoxon No paramétricas 𝑝𝑖ҧ 1 − 𝑝𝑖ҧ 𝑛 𝑛 Se rechaza H0 si: P[x<=x0/p=1/2]<α H1: 𝜇 > 𝜇0 , p>1/2 o 𝜇1-𝜇2>0 Se rechaza H0 si: P[x>=x0/p=1/2]<α H1: 𝜇 =! 𝜇0 , p=!1/2 o 𝜇1-𝜇2=!0 Se rechaza H0 si: 2P[x<=x0/p=1/2]<α H1: 𝜇 < 𝜇0 o 𝜇1-𝜇2<0 Se rechaza H0 si: T+ <=T0 H1: 𝜇 > 𝜇0 o 𝜇1-𝜇2>0 Se rechaza H0 si: T- <=T0 H1: 𝜇 =! 𝜇0 o 𝜇1-𝜇2=!0 , T=min(T+,T-) Se rechaza H0 si: T <=T0 𝑇1 =Suma de los rangos de la primera muestra H1: 𝜇1-𝜇2<0 Se rechaza H0 si: U2 <=U0 𝑇2=Suma de los rangos de la segunda muestra H1: 𝜇1-𝜇2>0 Se rechaza H0 si: U1 <=U0 H1: 𝜇1-𝜇2=!0 , U=min(U1,U2) Se rechaza H0 si: U <=U0 Se asigna "+" a cada valor mayor que µ0 y "-" a los menores (no se toman los iguales) X -- Binomial ( n , p=1/2) Ordenar los datos, restarles el µ0 y sumar los rangos de las restas positivas y de las negativas T0 se saca de la tabla T Wilcoxon para n y α 𝑛1 𝑛1 + 1 − 𝑇1 2 𝑛2 𝑛2 + 1 𝑈2 = 𝑛1 ⋅ 𝑛2 + − 𝑇2 2 𝑈1 = 𝑛1 ⋅ 𝑛2 + Mann - Whitney H1: 𝜇 < 𝜇0 , p<1/2 o 𝜇1-𝜇2<0 U0 se saca de la tabla de valores U de Mann - Whirney 𝑘 Kruskall - Walls 12 𝑅𝑖2 𝐻= ⋅ −3 𝑛+1 𝑛 𝑛+1 𝑛𝑖 𝑖=1 n = tamaño total de la muestra Ri = suma de los rangos de la muestra i ni = tamaño de la muestra i 2 𝐶 = 𝑋1−𝛼,𝐾−1 Se rechaza H0 si: H>C