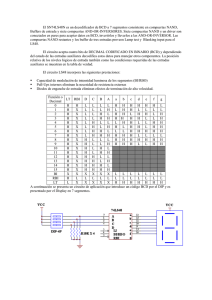
UNIVERSIDAD POLITECNICA SALESIANA INFORME DE ELECTRONICA DIGITAL Fecha: 11/11/2016 MULTIPLICADOR DE 2 BITS María Verónica Alba Valencia e-mail: malba@est.ups.edu.ec Erika Lorena Paltas Quimis e-mail: epaltas@est.ups.edu.ec Mario Henry Paucar Vasco e-mail: mpaucarv@est.ups.edu.ec CIRCUITOS COMBINACIONALES RESUMEN: En el informe se muestra el procedimiento para armar un circuito multiplicador de 2 bits en un protoboard utilizando compuertas lógicas, y luces led, que comprobarán el funcionamiento del circuito. Si el circuito está construido con puertas NAND, NOR su análisis se hace de forma análoga. REGLAS cuando el circuito está realizado con puertas NAND y queremos transformarlo en combinación de puertas AND y OR: Considérense como puertas OR todas las puertas NAND en nivel impar. Considérense como puertas AND todas las puertas NAND en nivel par. Compleméntense todas las variables que entren en el circuito en un nivel impar. Cuando una variable entre a un nivel par y a uno impar sólo será complementada en el nivel impar. [ CITATION MAR \l 3082 ]. PALABRAS CLAVE: Multiplicador d 2 bits, compuertas lógicas, luces led, fuente de corriente continua de 5v. 1. OBJETIVOS Realizar la simulación de un multiplicador de 2 bits con compuertas lógicas nand 7408. Analizar los diagramas lógicos armar el circuito en el protoboard. TABLAS DE VERDAD na tabla de verdad es una tabla que nos muestra la manera en que reacciona la salida de una compuerta o circuito lógico, en función de sus entradas. En la tabla se describen todas las posibles variables de entrada y las consiguientes variables de salida. 2. MARCOTEORICO COMPUERTAS LÓGICAS La construcción de las compuertas lógicas, está basada en componentes discretos (Transistores, Diodos, y Resistencias), pero con la enorme ventaja de que en un solo circuito integrado podemos encontrar 1, 2, 3 o 4 compuertas (dependiendo de su número de entradas y propiedades). Todos los circuitos internos de las compuertas están conectados de manera que las entradas y salidas puedan manejar estados lógicos (1 o 0). OPERACIONES LÒGICAS Las operaciones lógicas básicas son 3 OR (suma), AND (multiplicación) y NOT (negación), Tomando como base la operación que ejecutan, se le da a cada compuerta su nombre y símbolo en un diagrama. Pueden asimilarse a una calculadora, por un lado ingresas los datos, la compuerta realiza la operación lógica correspondiente a su tipo, y finalmente, muestra el resultado en algún display. COMPUERTA NAND Cada compuerta lógica realiza una operación aritmética o lógica diferente, que se representa mediante un símbolo de circuito. La operación que realiza (Operación lógica) tiene correspondencia con una determinada tabla, llamada “Tabla de Verdad”. Es el complemento de la función AND, como se indica por el símbolo gráfico, que consiste en una compuerta AND seguida por un pequeño círculo (quiere decir que invierte la señal). La designación NAND se deriva de la abreviación NOT - AND. Una designación más adecuada habría sido AND invertido puesto que es la función AND la que se ha invertido. Las compuertas NAND pueden tener más de dos entradas, y la salida es siempre el complemento de la función AND. 1 Ilustración 2 Símbolo esquemático de un Led Sìmbolo Gràfico 1 compuerta Nand A continuación se podrá observar en detalle cada uno de los pineados correspondientes a los circuitos integrados utilizados para la práctica. COMPUERTA NOR La compuerta NOR es el complemento de la compuerta OR y utiliza el símbolo de la compuerta OR seguido de un círculo pequeño (quiere decir que invierte la señal). Las compuertas NOR pueden tener más de dos entradas, y la salida es siempre el complemento de la función OR. 7400 Sìmbolo Gràfico 2 Compuerta Nor 7404 2.1 CIRCUITOS INTEGRADOS Existen dos formas para identificar el pin número 1. La primera, es un peque ˜no punto bajo relieve en el encapsulado plástico, ubicado justo sobre el pin ✟ ✠ 1. La segunda, es una indentación en el encapsulado, que se ubica a la izquierda, mirando el integrado desde arriba. En este caso, el pin nº 1 es el de más a la izquierda en la fila de abajo. El resto de los pines se cuentan en forma contraria a los punteros del reloj comenzando del pin nº 1, como se muestra en la figura. 7408 Ilustración 1 Ubicación del pin Nº 1 LEDs Los LED’s, light emitting diodes, se utilizan con frecuencia para indicar el nivel lógico de entradas y salidas digitales. Pueden conectarse para encender con una señal H (5 volts) o con una señal L (0 volts). La idea básica es conectar uno de los terminales del LED a la línea de poder, y el otro a la señal que se desea leer. Sin embargo, hay que tener en cuenta un par de detalles importantes. En primer lugar, los LED’s tienen polaridad, es decir, funcionan solo si se conectan en una dirección. Conectados al revés, no funcionan. 2 7432 7486 3. MATERIALES Y EQUIPO Protoboard Chips 7400 Chips 7408 Chips 7432 Chips 7805 Resistencias Cables DIP switch deslizable El circuito quedaría de la siguiente manera: 4. DESARROLLO Y PROCEDIMIENTO Se realiza una tabla de verdad y se resuelve por mapas de Karnaugth, de esta manera se podrá obtener la ecuación más simplificada para armar el circuito de manera óptima. 3 Realizamos la práctica: con anterioridad. 6. RECOMENDACIONES para entender mejor como funciona y así poder diseñar multiplicadores de 3, 4, o los bits que hagan falta, solo tienes que ver que números se están multiplicando en decimal, pasarlos a binario, y poner el resultado en binario. Un ejemplo: Queremos multiplicar el 2 y el 3, en decimal obtendríamos un resultado de 6, por lo que ya solo tendríamos que pasarlo a binario y obtendremos la solución:10 por 11 es igual a 0110. Una vez sabes esto ya puedes hacer la tabla de verdad y tendrás el multiplicador acabado. 7. REFERENCIAS Bibliografía 5. CONCLUSIONES En este proyecto se realizó el circuito de un multiplicador de dos números de 2 bits, que muestra el resultado se prende el LED de acuerdo a las configuraciones de la tabla de verdad que se realizó MARTINEZ, M. J. (s.f.). Circuitos Combinacionales. En M. J. MARTINEZ. mjmm@usal.es. 4