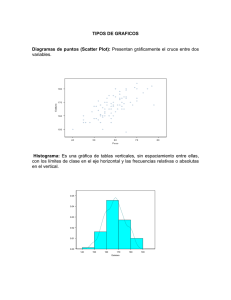
Distribuciones de Frecuencia Héctor Quintero Guillermo Bianchi Presentación de datos medidos en la escala Nominal u Ordinal Distribución de frecuencias Una tabla de clasificación o distribución de frecuencias permite mostrar como se clasifican los sujetos pertenecientes a una muestra o población de acuerdo a las modalidades, categorías o valores de una sola variable. Elementos de una Distribución de Frecuencias Ejemplo de Distribución de Frecuencias Ejemplo de Distribución de Frecuencias Distribución de Frecuencias para datos en escala Nominal Una distribución de frecuencias para datos medidos en la escala Nominal puede presentar las siguientes columnas de frecuencias: • Frecuencias simples (fi) absolutas • Frecuencias relativas simples expresadas en proporción o porcentaje. Frecuencias absolutas simples Las frecuencias absolutas simples indican el número de veces que se repite una modalidad, categoría o valor de la variable dentro del conjunto de datos. Las frecuencias absolutas se pueden calcular en cualquier escala de medición y se denotan como fi. Tabla 1. Sexo de los estudiantes Frecuencias relativas simples Las frecuencias relativas simples expresan la proporción (fri) o el porcentaje (%) de veces que se repite una modalidad, categoría o valor de la variable. Las frecuencias relativas simples se pueden calcular en cualquier escala de medición. Ejemplo Tabla 1. Clasificación de un grupo de estudiantes de la Facultad de Humanidades y Educación, según el sexo. Universidad de los Andes. Mérida - Venezuela, 2002. SEXO Femenino Masculino Total Fuente: Desconocida Frecuencia absoluta 9 19 28 Porcentaje 32,1 67,9 100,0 Distribución de Frecuencias para Datos en Escala Ordinal Una distribución de frecuencias para datos medidos en la escala Ordinal puede presentar las siguientes columnas de frecuencias: • Aquellas que se pueden presentar para datos medidos en la escala Nominal. • Frecuencias acumuladas (Fi) • Frecuencias acumuladas relativas en proporción (Fri) o porcentaje (R.P.) Frecuencias Absolutas Acumuladas La frecuencia absoluta acumulada de una categoría o valor de la variable indica la cantidad de sujetos que están en dicha categoría o las inferiores. Se denota como Fi y se puede calcular si los datos están medidos en la escala Ordinal, de Intervalo o de Razón. Frecuencias Relativas Acumuladas Las frecuencias acumuladas expresadas en proporción o porcentaje se definen como la proporción o el porcentaje de sujetos que están en una categoría o las inferiores. A las frecuencias acumuladas expresadas en porcentaje se les llama rangos percentiles. Ejemplo Tabla 2. Opinión de un grupo de estudiantes respecto a la calidad del servicio del comedor. Facultad de Humanidades y Educación, Universidad de los Andes, Mérida – Venezuela. Semestre A-2002. Opinión fi 4 Mala 5 Regular 11 Buena 8 Excelente 28 Total Fuente: Desconocida. fri 0,1428 0,1786 0,3929 0,2857 1,00 % 14,28 17,86 39,29 28,57 100 Fi 4 9 20 28 Fri 0,1428 0,3214 0,7143 1,00 R.P. 14,28 32,14 71,43 100 Tablas de Doble Entrada Se elabora una tabla de doble entrada cuando se tiene interés en clasificar a los sujetos de acuerdo a dos criterios o variables. En una tabla de doble entrada, las modalidades o categorías de una variable se colocan en la primera columna y las modalidades o categorías de la otra se colocan en la primera fila del cuerpo de la tabla. Ejemplo Partes de una tabla de doble entrada Nº de la tabla Título Variables Frecuencias Presentación Gráfica de Datos en Escala Nominal y Ordinal Tipos de gráficos Una variable • Sectores Circulares • Diagrama de Barras Simples Según el número de variables Dos variables • Diagrama de Barras Compuestas • Diagrama de Barras Agrupadas Elementos de un gráfico Título del gráfico. Debe indicar a los sujetos, las variables y la ubicación espacial y temporal Nº del gráfico Gráfico 2. Clasificación de un grupo de estudiantes de la Universidad Nacional Abierta de acuerdo a la tenencia de la vivienda. Mérida, octubre del 2000. Otra forma 8,6% Alquilada 22,3% Totalmente propia 50,2% Propia, pagándose 19,0% Datos supuestos Fuente o nota Diagrama de Sectores Circulares En un Diagrama de Sectores Circulares, el área de un círculo es usada para representar a la totalidad de los sujetos de una muestra o población. Gráfico 4. Mención de estudio de un grupo de estudiantes de la Escuela de Educación. Universidad de los Andes. Mérida, julio, 2004. Datos supuestos. 15% 5% 10% 25% 30% 15% Matemáticas B. Integral Cs. Físico N. Educ. Física Preescolar L. Modernas Diagrama de Barras Simples Gráfico 2. Estado civil de un grupo de estudiantes de la ULA. Mérida, Venezuela. Agosto, 2004. 80 60 Nº de estudiantes En un Diagrama de Barras Simples, se representa la frecuencia simple (absoluta o relativa) de cada modalidad o categoría de la variable mediante la altura de una barra. La altura de la barra es proporcional a la frecuencia de la categoría que representa. 40 20 0 Soltero Casado Divorciado Estado civil Concubino Diagrama de Barras Compuestas Un Diagrama de Barras Compuestas se utiliza para presentar la información contenida en una tabla de doble entrada. Gráfico 6. Clasificación de un grupo de habitantes de la ciudad de Mérida según el género y su evaluación sobre la calidad de la tv venezolana. Venezuela, Agosto, 2004. Fuente: Instituto Nacional de Estadística. 140 120 100 80 Masculino Femenino 60 40 20 0 Mala Regular Evaluación Buena Excelente Diagrama de Barras Compuestas En este tipo de gráfico, las dos variables se representan con el siguiente criterio: 2.La altura de las barras representan la frecuencia simple de las modalidades o categorías de una variable. 3.Cada una de las barras es dividida en tantos segmentos como modalidades o categorías tenga la otra variable, siendo la altura de estos segmentos proporcional a la frecuencia simple de cada modalidad o categoría. Ejemplo de Diagrama de Barras Compuestas Gráfico 6. Clasificación de un grupo de habitantes de la ciudad de Mérida según el género y su evaluación sobre la calidad de la tv venezolana. Venezuela, Agosto, 2004. Fuente: Instituto Nacional de Estadística. 140 120 100 80 Masculino Femenino 60 40 20 0 Mala Regular Evaluación Buena Excelente Diagrama de Barras Agrupadas Al igual que el Diagrama de Barras Compuestas, un Diagrama de Barras Agrupadas se utiliza para presentar la información contenida en una tabla de doble entrada; es decir, se utiliza para representar la información obtenida a partir de la medición de dos variables. Diagrama de Barras Agrupadas En este tipo de gráfico se muestra, mediante un conjunto de barras, como se clasifican los sujetos respecto a las distintas modalidades o categorías de una variable dentro cada modalidad o categoría de la otra variable. Gráfico 7. Clasificación de un grupo de habitantes de la ciudad de Mérida según el género y su evaluación sobre la calidad de la tv venezolana. Venezuela, Agosto, 2004. Fuente: Instituto Nacional de Estadística. 100 90 80 70 60 50 40 30 20 10 0 Femenino Masculino Mala Regular Evaluación Buena Excelente Ejemplo Diagrama de Barras Agrupadas Gráfico 8. Clasificación de un grupo de habitantes de Mérida según Nª de habitantes el género y la frecuencia de visualización de telenovelas. Estado Mérida, Venezuela. Agosto, 2004. 350 300 314 250 236 200 195 150 100 158 140 118 118 Género 117 Masculino 50 48 0 N n u e m a c ra s s te ía a a te s ía n n d d e m s a o ri a a ri o ri ia a R V V D l m la s e m e s Frecuencia de visualización Datos Supuestos. 46 Femenino Presentación de Datos Cuantitativos Distribuciones de frecuencias Usando los valores de la variable Distribuciones de frecuencias para datos cuantitativos Usando intervalos de clase Distribución de Frecuencia usando los valores de la variable Tabla 1. Distribución del número de hijos de un grupo de estudiantes de la Escuela de Educación. Universidad de los Andes, núcleo Mérida. Noviembre, 2004. Nº de hijos Frecuencia 0 25 1 8 2 5 Total 38 Fuente: Desconocida Distribuciones de Frecuencia usando intervalos de clase Tabla 2. Edades (en años cumplidos) de un grupo de estudiantes de la Escuela de Educación. Universidad de los Andes, núcleo Mérida. Noviembre, 2004. Edad Frecuencia 16 - 18 15 19 - 21 20 22 - 24 14 25 - 27 10 28 - 30 5 31 - 33 4 Total 68 Fuente: Desconocida ¿Cuándo usar los valores de la variable? Se recomienda agrupar los datos usando los valores de la variable cuando ésta asume solo unos pocos valores. Tal es el caso, por ejemplo, del número de hijos o el número de hermanos. ¿Cuándo usar intervalos de clase? Se recomienda usar intervalos de clase cuando los datos presentan una gran variabilidad, es decir, pueden asumir una gran cantidad de valores. Tal es caso, por ejemplo, de la edades, el peso, la estatura, el ingreso mensual familiar, etc. Frecuencias Simples y Acumuladas Si la variable está medida en una escala de Intervalo o de Razón es posible calcular todas las frecuencias simples y acumuladas que se indicaron para las variables medidas en las escalas Nominal y Ordinal. Ejemplo Tabla 2. Edades (en años cumplidos) de un grupo de estudiantes de la Escuela de Educación. Universidad de los Andes, núcleo Mérida. Noviembre, 2004. Edad (Límites aparentes) ni fi % Ni Fi R.P. Puntos medios (Xi) Límites reales 16 - 18 19 - 21 22 - 24 25 - 27 28 - 30 31 - 33 Total 15 20 14 10 5 4 68 0,22 0,29 0,21 0,15 0,07 0,06 1,00 22 29 21 15 7 6 100 15 35 49 59 64 68 0,22 0,51 0,72 0,87 0,94 1,00 22 51 72 87 94 100 17 20 23 26 29 32 15,5 – 18,5 18,5 – 21,5 21,5 – 24,5 24,5 – 27,5 27,5 – 30,5 30,5 – 33,5 Fuente: Desconocida Puntos Medios. Definición. Los puntos medios de un intervalo se definen como la semi-suma de los límites aparentes del intervalo. L. A.I + L. A.S Xi = 2 Los puntos medios o marcas de clase se usan para realizar cálculos que involucran a los valores de la variable, tales como la media aritmética o la desviación típica. Límites Reales de una Clase Todo intervalo tiene dos límites reales: Límite real inferior: unidad L.R.I = L. A.I − 2 Límite real superior: unidad L.R.S = L. A.S + 2 Presentación Gráfica de Datos Cuantitativos. Histograma Polígono de frecuencias Una variable Ojiva porcentual Dos variables Diagrama de dispersión Gráficos para datos cuantitativos Histograma Un Histograma es una herramienta útil cuando se quiere mostrar en forma gráfica la información contenida en una distribución de frecuencias para datos agrupados en intervalos de clase. En un Histograma se usan barras para presentar el número de casos de cada clase o intervalo. La altura de cada barra es proporcional a la frecuencia absoluta de la barra que representa. Histograma Gráfico 1.Estatura de un grupo de estudiantes de la Escuela de Educación Univ ersidad de los A ndes, Mérida. Nov iembre, 2004. 200 Nº de estudiantes 1 80 1 88 1 60 1 40 1 20 110 1 00 80 71 60 58 40 31 20 0 16 15 6 8 1, 0 8 1, 5 7 1, 9 6 1, 4 6 1, 3 5 8 5 1, 1, 7 4 1, 0 5 0 5 0 5 0 5 - - - - - - - - 15 9 1, 5 0 0 8 1, 0 6 8 5 7 1, 5 1, 9 6 1, 5 0 8 5 1, 0 4 6 1, 3 5 1, Estatura Polígono de Frecuencias El polígono de frecuencias consiste en un gráfico de líneas usado para presentar la frecuencia absoluta de los valores de una distribución. La altura del punto asociado a un valor de la variables es proporcional a la frecuencia de dicho valor. Polígonos de Frecuencia Ojiva Porcentual La ojiva porcentual es un gráfico acumulativo que se conoce también con los nombres de curva de porcentajes acumulados u ojiva. La Ojiva es útil cuando se quiere presentar el rango percentil de cada valor en una distribución de frecuencias: la altura del punto asociado a un valor es proporcional a su rango percentil o porcentaje acumulado. Ojiva Porcentual Gráfi co 3. Edad (en años cumpli dos) de un grupo de estudi antes de la Escuela de Educaci ón. Uni versi dad de los Andes, Méri da. Novi embre, 2004. Porcentaje acumulado 100 80 60 40 20 0 23 27 29 30 31 32 33 Edad (en años cumpli dos) Fuente: Desconoci da 34 35 36