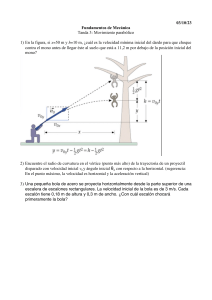
Conceptos de sentido común sobre el movimiento Ibrahim Abou Hallouna) and David Hestenes (In: Am. J. Phys. 53 (11), November 1985) Department of Physics, Arizona State University, Tempe, Arizona 85287 Resumen: Se estudian y analizan las creencias de sentido común de los estudiantes universitarios sobre el movimiento y sus causas. Una taxonomía de conceptos de sentido común que entran en conflicto con la teoría newtoniana se desarrolla como una guía para la instrucción. En el artículo anterior, establecimos la necesidad de una instrucción en física que tenga en cuenta las creencias iniciales del sentido común (SC) de los estudiantes. Otros investigadores [2-9] han identificado creencias específicas de SC que entran en conflicto con la teoría newtoniana e interfieren con la instrucción en física. Pero se necesita una taxonomía más sistemática y completa de las creencias de SC para un diseño instruccional eficiente. El propósito de este artículo es estudiar y categorizar los conceptos de movimiento de SC que deben tenerse en cuenta en la instrucción de mecánica. Nuestro objetivo es obtener una imagen completa de los conceptos de SC que incluye los conocimientos de investigaciones anteriores, así como algunas observaciones propias. En este artículo no abordaremos el difícil problema de diseñar instrucciones para acomodar las ideas preconcebidas de SC. Pero notemos que los conceptos de SC no pueden evitarse en la instrucción de física, ya que el sentido común es una codificación de experiencia que proporciona significado a nuestro lenguaje natural. El discurso sobre la física sería imposible sin eso. De hecho, la física y la ciencia en general pueden considerarse como una extensión y modificación del sentido común. La instrucción física convencional apela tácitamente al conocimiento de sentido común, pero los estudiantes tienen problemas cuando ese conocimiento es defectuoso. Es difícil para los estudiantes determinar exactamente qué conocimiento de sentido común son confiables sin una crítica explícita de los conceptos de SC. Nuestra encuesta sobre conceptos de movimiento de SC tiene la intención de proporcionar una base para dicha crítica. Las creencias de SC que son incompatibles con la teoría científica establecida son etiquetados rápidamente como "conceptos erróneos" y descartados por la mayoría de los científicos. Pero los estudiantes no son tan fácilmente desengañados de las creencias del SC, porque sus propias creencias se basan en una larga experiencia personal. Los conceptos erróneos de SC no son errores arbitrarios o triviales. De hecho, cada uno de los conceptos erróneos sobre el movimiento común entre los estudiantes de hoy fue defendido seriamente por los principales intelectuales en los tiempos pre-newtonianos. Los historiadores [10-14] nos cuentan sobre la larga y difícil crítica y análisis de las creencias de SC que prepararon el camino para la "revolución newtoniana". Si la evaluación del sentido común fue tan difícil para los gigantes intelectuales desde Aristóteles hasta Galileo, no debería sorprendernos ver que es un problema para los estudiantes corrientes de hoy. En consecuencia, las creencias de sentido común deben ser tratadas con respeto genuino por parte de los instructores. Deben considerarse como hipótesis alternativas serias para ser evaluadas por procedimientos científicos. Esto proporcionaría a los estudiantes razones sólidas para modificar sus creencias más allá de la mera autoridad del maestro y el libro de texto. Los historiadores no han dejado de observar que las grandes luchas intelectuales del pasado proporcionan valiosos conocimientos sobre las dificultades conceptuales de los estudiantes. En consecuencia, defienden una fuerte dosis de historia para el plan de estudios de física. I. Bernard Cohen, por ejemplo, ha escrito un libro notable [11] sobre la historia temprana de la mecánica para estudiantes de secundaria. Pero el plan de estudios deja poco espacio para la historia de la ciencia, por lo que los temas de estudio deben ser elegidos juiciosamente. Temas de gran interés histórico pueden tener un valor pedagógico limitado. Por ejemplo, el auge y la caída de la teoría ptolemaica es uno de los temas históricos más comunes, pero no se ocupa de cuestiones conceptuales que molestan a los estudiantes. Por otro lado, los conceptos erróneos aristotélicos sobre la caída libre son comunes entre los estudiantes y difíciles de rectificar. Como antecedentes históricos para ver las creencias SC de los estudiantes contemporáneos, algunas ideas importantes de la física pre-newtoniana se revisan en Secs. II y III. Confesamos algunas simplificaciones excesivas del registro histórico en nuestro esfuerzo por separar los hechos históricos con relevancia pedagógica. En Sec. IV informamos sobre nuestras propias observaciones de creencias de SC sostenidas por estudiantes universitarios. Confirman los resultados de investigaciones anteriores, especialmente sobre la prevalencia de los conceptos de Impetus. Finalmente, en Sec. V presentamos una taxonomía de creencias SC para ser utilizada como una guía para el diseño instruccional. II. FÍSICA ARISTOTÉLICA Aristóteles fue el primero en desarrollar sistemáticamente formulaciones explícitas para las creencias de CS sobre los fenómenos físicos y organizarlos en un sistema conceptual coherente. Por lo tanto, preparó el camino para una crítica de las creencias SC que contribuyeron al desarrollo de la ciencia física. El largo tiempo de gestación para la ciencia muestra cuán difícil fue detectar y corregir los defectos en el sistema aristotélico. Los sistemas de creencias de los estudiantes no instruidos en física a veces se caracterizan como "aristotélicos". El término es inapropiado. No solo el sistema aristotélico es mucho más elaborado y lógicamente consistente, sino que los sistemas de creencias de la mayoría de los estudiantes están más cerca de la teoría medieval de ímpetu, que discutiremos más adelante. Muchos estudiantes tienen algunas creencias aristotélicas. Pero para fines pedagógicos, es aconsejable ser específico acerca de estas creencias. Aristóteles separó la cosmología del resto de la física, y se separaron hasta la "síntesis newtoniana". La cosmología aristotélica está muy alejada del pensamiento de los estudiantes de hoy en día, por lo que podemos restringir nuestra atención a la física terrestre de Aristóteles. Más específicamente, consideramos solo su teoría del movimiento. Aristóteles definió el movimiento como un cambio de posición, y reconoció la necesidad de un marco de referencia con respecto al cual el movimiento se observa. Sus argumentos de que la superficie de la tierra debe estar en reposo no se le ocurrirán al estudiante típico, que cree que la tierra está girando solo porque le han dicho. Sin embargo, puede valer la pena presentar los argumentos con toda su fuerza a los estudiantes de física para que los refuten. Esa sería una prueba importante de su comprensión de la mecánica newtoniana. Para este propósito, la cuenta de Cohen [11] puede ser útil. Aristóteles consideraba el movimiento en el vacío como una abstracción poco realista. Él apoyó esta opinión con varios argumentos diferentes. En particular, argumentó que el movimiento en el vacío sería imposible. Sus argumentos no parecen ser de interés pedagógico. El punto importante es que su teoría del movimiento trata solo con cuerpos inmersos en un medio material. Para Aristóteles, el descanso es el "estado natural" de todos los objetos, y cada movimiento tiene una causa. Aristóteles reconoció dos tipos de causa o fuerza: (1) una fuerza o tendencia inherente de cada objeto para buscar su lugar natural y (2) una fuerza de contacto (empujar o tirar) ejercida por algún agente externo (objeto o medio). Él no admitió fuerzas de largo alcance. La tendencia inherente de un objeto a moverse hacia su lugar natural depende de su composición. Los cuerpos pesados, compuestos principalmente de tierra y agua, están dotados de la propiedad de la gravedad, una tendencia centrípeta a moverse hacia el centro del universo. Los cuerpos ligeros, compuestos principalmente de aire y fuego, están dotados de la propiedad de la levedad, una tendencia centrífuga a huir del centro del universo. Todo esto, evidentemente, está muy alejado de las creencias CS de los estudiantes de hoy, excepto por la noción de que la gravedad es una tendencia a la caída de objetos pesados. Sin embargo, muchos estudiantes comparten con Aristóteles la creencia de que la velocidad de un cuerpo que cae es proporcional a su peso W. Al igual que Aristóteles, su única medida de movimiento es la velocidad promedio. Entonces, la velocidad v de un objeto que ha caído una distancia D desde el reposo en el tiempo T viene dada por v = D/T. (1) Aristóteles discutió la resistencia de un medio en detalle e infirió que la velocidad es inversamente proporcional a la resistencia R, que depende del tamaño y la forma del cuerpo, así como de la densidad del medio. Así, en un sistema apropiado de unidades (que Aristóteles nunca discute), la ley de Aristóteles de cuerpos que caen puede escribirse como v=W/R. (2) En consecuencia, para dos cuerpos del mismo tamaño y forma liberados simultáneamente desde el reposo, en cualquier momento la relación de velocidades está dada por v1/v2 = D1/D2 = W1/W2. (3) En otras palabras, el cuerpo más pesado cae más rápido (más lejos) en proporción a su peso. Por supuesto, la ley de Aristóteles no es verdadera, pero tampoco lo es la ley de Galileo (para cuerpos que caen a través de un medio). Como advertencia histórica, debe mencionarse que la física de Aristóteles era más cualitativa que cuantitativa. De hecho, él creía que la física cuantitativa es imposible. Sin embargo, las Ecs. (1) y (2) son formulaciones algebraicas directas de sus afirmaciones cualitativas, y las relaciones expresadas por la ecuación (3) fueron inferidas y discutidas por sus seguidores en la Edad Media. Pasemos ahora a la otra clase de fuerza en la teoría de Aristóteles. Una fuerza externa puede ser ejercida sobre un objeto solo por un agente vivo en contacto directo con ella o indirectamente a través de alguna conexión, como una cuerda. Las cosas no vivas son obstáculos que detienen o guían el movimiento, pero no ejercen fuerzas. Una fuerza no mueve un objeto a menos que supere (exceda) la inercia del objeto, una resistencia intrínseca (masa) que no se distingue del peso. Una fuerza constante F imparte al objeto una velocidad constante v, que es inversamente proporcional a la resistencia R, dependiendo del medio así como de la inercia del objeto. En forma algebraica desconocida en los días de Aristóteles, esto puede escribirse como v=F/R (4) De acuerdo con esta ley, los seguidores de Aristóteles concluyeron que un aumento en la velocidad (aceleración) se puede lograr mediante un aumento en la fuerza, o, en el caso del movimiento natural (caída libre), mediante un aumento de peso a medida que el objeto se pone más cerca de su lugar natural. Aristóteles supuso que, en ausencia de cualquier fuerza, un objeto se detiene inmediatamente. Entonces, para explicar fenómenos como el vuelo de una flecha, se vio obligado a atribuir motivos y poderes de resistencia a un medio. Por lo tanto, la flecha es impulsada por el aire que se colapsa detrás de ella y así se transmite, por supuesto, la fuerza ejercida por el agente viviente que dibujó el arco. La crítica de su argumento ad hoc conduce a una revisión de la teoría aristotélica en la Edad Media, a la que ahora nos referimos. III. FÍSICA DEL ÍMPETU La idea de Aristóteles de que un medio tiene un poder motriz se introdujo para explicar la persistencia del movimiento en ausencia de un agente externo, de acuerdo con el principio general de que todo movimiento tiene una causa. Esta idea fue rechazada a favor de una explicación alternativa de Johannes Philoponus de Alejandría, un filósofo y comentarista de Aristóteles. Propuso que cuando se arroja un objeto, el agente activo imparte al objeto un cierto poder motriz inmaterial que sostiene el movimiento del cuerpo hasta que se haya disipado debido a la resistencia del medio. Esta fuerza motriz transmitida fue llamada ímpetu por Jean Buridan, quien fue responsable de la formulación definitiva de la teoría del ímpetu en el siglo XIV. Ímpetu es un concepto de CS tan natural que alguna versión de él ocurre a una fracción sustancial de los estudiantes de hoy en día [3], que usualmente se refieren a él como una fuerza y tienden a confundirlo con el concepto de fuerza newtoniano. La formulación de Buridan del concepto de ímpetu es una articulación tan clara de las intuiciones más o menos vagas comunes entre los estudiantes que vale la pena citar [15]: "Un motor, al mover un cuerpo, le imprime un cierto ímpetu, un cierto poder capaz de mover este cuerpo en la dirección en que el motor lo pone en marcha, ya sea hacia arriba, hacia abajo, de costado o en círculo. Por la misma cantidad que el motor mueve el mismo cuerpo rápidamente, en esa cantidad es el ímpetu que está impresionado en él. Es por este impulso que la piedra se mueve después de que el lanzador deja de moverlo, pero debido a la resistencia del aire y la gravedad de la piedra, que la inclina a moverse en una dirección opuesta a la dirección hacia la cual el ímpetu tiende a moverla, este ímpetu se debilita continuamente. Por lo tanto, el movimiento de la piedra será cada vez más lento y, por fin, el ímpetu disminuyó o destruyó ya que la gravedad de la piedra prevalece sobre ella y mueve la piedra hacia su lugar natural". Tenga en cuenta que esta afirmación incluye la posibilidad de un ímpetu circular, que Buridan usó para explicar el movimiento persistente de los planetas y la rueda de la amoladora. Tenga en cuenta también que la idea de ímpetu puede explicar el movimiento en el vacío, y por lo tanto supera los principales argumentos de Aristóteles contra la posible existencia de un vacío. El concepto de ímpetu es un precursor histórico de los conceptos de momento y energía cinética. Tuvo una influencia significativa en el pensamiento de Galileo, tal como enfatizó Clement [2 ]en un contexto pedagógico. Albert de Sajonia utilizó la teoría de Buridan para explicar el movimiento del proyectil. Esto implica un compromiso entre los efectos del ímpetu, la gravedad y la resistencia del aire. Para un proyectil lanzado horizontalmente, la Fig. 1 muestra la trayectoria de tres etapas que él dibujó [16]. Como explicó, en la etapa inicial (a), el ímpetu suprime cualquier efecto de la gravedad y propulsa el proyectil horizontalmente hasta que se debilita lo suficiente por la resistencia del aire. La etapa intermedia (b) muestra un compromiso entre el ímpetu y la gravedad hasta que se agota el ímpetu inicial, y en la etapa final (c), el proyectil cae verticalmente en "movimiento natural". Un Fig. 1. La trayectoria del proyectil de Albert de Sajonia razonamiento similar es exhibido por los estudiantes en esta edad, como veremos. Varias ideas cinemáticas importantes se desarrollaron en el siglo XIV junto con la teoría del ímpetu: (a) se hizo una distinción clara entre la velocidad uniforme, la aceleración uniforme y la aceleración no uniforme, que dio origen a los conceptos de velocidad y aceleración instantánea. Esto muestra que una comprensión cualitativa de estos conceptos es posible sin formalismo matemático, y por lo tanto sugiere un objetivo pedagógico digno. (b) Oresme inventó el método gráfico para representar cantidades variables. (c) Esto se usó para derivar la "regla de velocidad media" de Merton, que dice que en un intervalo de tiempo dado, la distancia recorrida con aceleración uniforme es igual a la distancia recorrida con una velocidad uniforme igual a la velocidad instantánea en el movimiento acelerado en el instante medio del intervalo de tiempo. Todas estas ideas eran requisitos previos esenciales para el análisis cinemático de Galileo del movimiento de proyectiles. Tenemos mejores medios simbólicos para representar estos conceptos en la actualidad, pero la historia ayuda a revelar las dificultades para establecer una base firme e intuitiva para los conceptos. IV. CONCEPTOS DE SENTIDO COMUN DE ESTUDIANTES UNIVERSITARIOS Para estudiar los conceptos sobre el movimiento de estudiantes universitarios matriculados en cursos de física, utilizamos una prueba de diagnóstico de mecánica de opción múltiple y realizamos entrevistas con una muestra de 22 estudiantes en el plazo de un mes después de haber realizado el examen. Se muestra una copia de la prueba de diagnóstico completa en el Apéndice del documento anterior, 1 y en la discusión a continuación nos referiremos con frecuencia a tareas específicas en la prueba. Las condiciones bajo las cuales se realizó la prueba y el desempeño promedio de los estudiantes se informaron anteriormente. Aquí analizamos las respuestas a preguntas específicas. Todas las estadísticas que se incluyen a continuación corresponden a un grupo de 478 estudiantes de física universitaria. Los resultados del pre-test (pos-test) se obtuvieron mediante la administración de la prueba de diagnóstico al comienzo (final) del semestre. Las alternativas de opción múltiple a varias de las preguntas en la prueba de diagnóstico se clasifican fácilmente como características de las teorías aristotélicas, ímpetu o newtonianas. Esto nos permitió clasificar las respuestas de la prueba como predominantemente aristotélicas para el 18% de los estudiantes, predominantemente del tipo ímpetu para el 65% de los estudiantes, y predominantemente newtonianos para el 17% restante. Sin embargo, casi todos los estudiantes usaron alguna combinación de conceptos de las tres teorías, y parecían ser inconsistentes al aplicar el mismo concepto en diferentes situaciones. Por ejemplo, (a) En el pre-test (pos-test), el 47% (20%) de los estudiantes mostraron, al menos una vez, la creencia de que, sin fuerza neta, un objeto se ralentiza. Sin embargo, solo el 1% (0%) mantuvo esa creencia en tareas similares. (b) Alrededor del 66% (54%) de los estudiantes sostuvo, al menos una vez, la creencia de que bajo una fuerza constante un objeto se mueve a velocidad constante. Sin embargo, solo el 2% (1%) mantuvo esa creencia de manera consistente. (c) Alrededor del 65% (44%) de los estudiantes exhibieron, al menos una vez, la creencia de que se requiere un ímpetu para mantener el movimiento de un objeto. Alrededor del 40% (24%) fueron consistentes en esa creencia. Alrededor del 37% (15%) mantuvo, al menos una vez, que la trayectoria de un objeto depende de un ímpetu impresionado, pero solo el 3% (1%) fue consistente en esta creencia. Los estudiantes con creencias cuasi-newtonianas fueron mucho más consistentes que los otros estudiantes. Los sistemas conceptuales de CS de los estudiantes tienen mucha menos coherencia interna que los sistemas aristotélicos e impetuosos. Se pueden describir mejor como conjuntos de conceptos poco relacionados y a veces inconsistentes. Por ejemplo, aunque el 84% de los estudiantes evaluados previamente creían que una partícula libre sigue una trayectoria lineal, solo el 30% cree que la velocidad de dicha partícula es constante. Además, solo el 15% de los estudiantes tenían la creencia newtoniana de que bajo una fuerza constante una partícula tiene una aceleración constante. Sin duda, gran parte de la incoherencia en los sistemas de CS de los estudiantes es el resultado de conceptos vagos e indiferenciados. En la prueba preliminar, el 82% de los estudiantes creían que las propiedades geométricas y físicas intrínsecas de un objeto afectan su caída libre en el vacío. Casi todos estos estudiantes tenían mezclas de creencias aristotélicas y de ímpetu. De estos estudiantes, el 83% no reconoció la alta simetría en la tarea (X) del test de diagnóstico, y el 61% confundió los conceptos de posición, velocidad y aceleración al menos una vez. Tales conceptos erróneos eran raros entre los estudiantes que sabían que las propiedades intrínsecas de un objeto no afectan su caída libre. Para investigar más profundamente las creencias de sentido común, se entrevistó a 22 estudiantes sobre sus respuestas en la prueba de diagnóstico. Los estudiantes invariablemente reiteraron las respuestas que habían dado anteriormente y fueron lentos para cambiarlas a medida que las preguntas se discutían con mayor profundidad. Se les pidió a los estudiantes que justificaran sus respuestas y opiniones, y el entrevistador introdujo reiteradamente información contraria y pidió comparaciones entre diferentes situaciones físicas en un esfuerzo por probar la estabilidad de las creencias de los estudiantes. Durante las entrevistas con varios de los estudiantes, se dieron demostraciones típicas en el aula de las situaciones físicas descritas en algunas de las charlas sobre la prueba de diagnóstico. Las manifestaciones parecían no tener más efecto en sus opiniones que simples discusiones sobre los fenómenos. Como regla general, los estudiantes se mantuvieron firmes ante creencias erróneas incluso cuando se enfrentaban a fenómenos que contradecían esas creencias. Cuando se reconocía o señalaba una contradicción, al principio tendían a no cuestionar sus propias creencias, sino a argumentar que la instancia observada estaba gobernada por alguna otra ley o principio y el principio que usaban se aplicaba a un caso ligeramente diferente. Un estudiante argumentó que en la tarea (IV), la bola después del lanzamiento comienza su movimiento en un arco circular antes de tomar la ruta parabólica correcta. Después de observar el movimiento de una pelota en el aire liberado de un brazo electromagnético que gira uniformemente en un círculo vertical, sostuvo que, a pesar de ver a la pelota seguir una trayectoria parabólica, la "bola oscilará de la misma manera que antes de que se desconectó por un corto mientras ... [que] no podemos ver a simple vista ". Otro estudiante había argumentado a favor de un camino recto en la pregunta (26) de la tarea (IX). Después de ver un movimiento parabólico simulado de un disco sobre una mesa de aire, argumentó que "si la mesa fuera lo suficientemente larga, el disco eventualmente pasaría directamente ... tal vez incluso en la dirección del aire [soplado de una manguera en el puck] ... después de que la fuerza debida al aire supera la velocidad inicial que tomaría el disco en esta dirección [la del cohete antes de que se dispararan los motores] ". Las entrevistas cuidadosas de los estudiantes que acaban de presenciar una manifestación son suficientes para poner en duda la efectividad de las típicas demostraciones de física en el aula al alterar las creencias físicas erróneas. Dudamos de que una demostración pueda ser efectiva a menos que se realice en un contexto que provoque y ayude a resolver conflictos entre el sentido común y conceptos científicos específicos. Después de largas discusiones, la mayoría de los estudiantes que mostraron creencias obstinadas fueron capaces de justificar algunos, principalmente no porque hayan visto algo en conflicto con sus creencias, sino porque se dieron cuenta de la inconsistencia de su pensamiento cuando se les pidió que reflexionasen sobre sus propios argumentos. Para estudiar la variedad de conceptos estudiantiles de manera ordenada, hemos catalogado nuestros resultados de A a D en la Sec. IV que sigue. A. Conceptos generales sobre el movimiento Esta subsección se refiere principalmente a cómo los estudiantes "definen" sus conceptos de fuerza, gravedad y movimiento. Las subsecciones subsecuentes se ocuparán de cómo usan los conceptos para explicar los efectos dinámicos. La mayoría de los estudiantes entrevistados habían adquirido un conocimiento de memoria de las leyes de Newton, ya sea del curso de física en el que se inscribieron en ese momento o de un curso anterior. Podrían enunciar las leyes de Newton a petición, pero por lo general no podían ver cómo se aplicaban las leyes a una pregunta en particular. Cuando se le pidió que justificara por qué un proyectil sigue una ruta parabólica, un estudiante respondió: "No sé. Me han enseñado que va en una parábola, pero nunca entendí por qué". En la vida cotidiana, el término "fuerza" se usa en una variedad caótica de contextos: fuerza policial, fuerza económica, fuerza de argumentación, a menudo con asociaciones vagas y ambiguas. Por lo tanto, es de esperar que los estudiantes principiantes sean propensos a usar el término "fuerza" libremente para una variedad de conceptos diferentes, algunos de los cuales ni siquiera son dinámicos. Un estudiante afirmó que "la aceleración es una fuerza. Suena como una fuerza". En la prueba preliminar, el 65% de los estudiantes mantuvo la creencia precientífica de que "cada movimiento tiene una causa". En su búsqueda de una causa de movimiento, los estudiantes entrevistados dieron los siguientes nombres a una supuesta causa: “Una fuerza de inercia". "Una fuerza potencial". "La fuerza de la velocidad". "La velocidad crea una fuerza". "Energía o fuerza a la que le disparaste". "Todavía tiene algo de fuerza dentro". "La fuerza detrás de esto... viniendo del lanzamiento". "El poder también tiene una fuerza". Algunos estudiantes compararon la magnitud de una fuerza con las magnitudes de los conceptos cinemáticos: "La velocidad es igual a la fuerza de tracción". "La velocidad inicial es mayor que la fuerza". "La energía del estallido tiene que ser mayor que la fuerza". Los estudiantes no usaron una clasificación de fuerzas Newtoniana. Más bien, ellos distinguieron una fuerza que: "solo comienza la moción" o "solo está cambiando la dirección del movimiento" o "No tiene nada que ver con [cambiar] la velocidad, solo tiene que mantener la pelota en movimiento". Para algunos estudiantes, el efecto de una fuerza puede no aparecer en el instante en que se aplica, o el efecto puede ser autoconsumido o disipado por resistencias externas: "La fuerza actúa solo después de... haber superado la velocidad inicial". "Esta fuerza no puede quedarse para siempre... Nada permanece para siempre". "El cañón tiene la fuerza suficiente para llevar [una bala de cañón] solo tan lejos". "La fuerza disminuye... debido a la atracción de la gravedad en la dirección [opuesta]” Muchos estudiantes creen que los objetos inanimados pueden servir como barreras para detener o redirigir el movimiento, pero no como agentes de una fuerza. Como explicó un estudiante, "Hubo una fuerza cuando sostenías [una pelota] en tu mano... [Pero cuando la pelota está sentada sobre una mesa], no hay una fuerza sobre la pelota... esto es diferente. La pelota quiere bajar, pero la mesa solo la sostiene... evitando que se mueva". El mismo estudiante argumentó que no se requiere una fuerza para que los objetos caigan, ya que "siempre quieren bajar". Como explicó, "no hay fuerza sobre la bola [cayendo]... Había una fuerza cuando la sostenías, pero cuando la dejas ir, no hay más fuerza y la bola puede caerse...la bola quiere bajar, pero la sostienes... así que cuando la dejas ir, vuelve al suelo, y ahí está la gravedad". Aquí el entrevistador intervino para preguntar si la gravedad es una fuerza; el estudiante respondió: "No, no sé... supongo que no, ya que [después de lanzar una pelota] se acelera por un corto tiempo... para alcanzar la velocidad de caída. Entonces la pelota debe ir a velocidad constante porque no hay fuerza para detenerlo o tal vez para acelerarlo... Así que supongo que no, la gravedad no es una fuerza ". Algunos estudiantes creen que la gravedad es un tipo de ímpetu adquirido por la caída de objetos. Como dijo un alumno, "la gravedad aumenta a medida que los objetos caen... porque su velocidad se hace cada vez mayor". Escucharemos más de esta idea más adelante. Todos los estudiantes entrevistados aceptaron la existencia de un vacío, pero algunos sostuvieron que el movimiento es imposible en ausencia de un medio material. Como explicó un estudiante, "Si liberas un cuerpo en el vacío, se queda donde está... No hay movimiento en el vacío... porque la gravedad no actúa en el vacío. La gravedad actúa solo si hay aire... un cuerpo se mueve hacia abajo debido al aire que empuja hacia abajo sobre el cuerpo... El aire también empuja en todas direcciones, esto es fricción... Pero el empuje hacia abajo es mayor que la fricción y es por eso que un cuerpo cae". "Cuanto más pesado es un cuerpo, menor es el efecto de la fricción... La masa de un cuerpo ayuda al aire a empujar hacia abajo... [En el agua, la velocidad de caída es menor que en el aire] porque la fricción en el agua es mayor que en el aire. El agua empuja hacia abajo más que el aire, pero la velocidad es menor porque la fricción en el agua tiene un efecto mayor que en el aire [debido a la densidad del agua], más grande que el empuje hacia abajo". Con respecto a los aspectos cinemáticos del movimiento, el problema más común y crítico para los estudiantes fue la imposibilidad de discriminar entre las diversas cantidades cinemáticas. Esto fue claro entre los estudiantes entrevistados, aunque la mayoría de ellos ya había completado un estudio de cinemática en sus clases de física. Más del 30% de los estudiantes mantuvieron en el ensayo previo que dos partículas tienen la misma velocidad cuando ocupan simultáneamente la misma posición, incluso si las dos partículas se movían con diferentes velocidades constantes. Cuando los entrevistados no justificaron o refutaron su concepto erróneo, se les pidió que asumieran que las dos partículas [tarea (I) de la prueba de diagnóstico] se mueven con velocidades constantes de 10 y 15 mph, respectivamente. Luego se les preguntó cuál sería la velocidad común de las dos partículas en el instante en que se encontraron. Un estudiante respondió: "Dado que se encontraron en la [posición 2 de la tarea (I)], ambos deberían tener la misma velocidad... Es un valor entre 10 y 15 mph". [Cuando se les recuerda que las dos bolas se mueven con velocidades constantes], "entonces supongo que no pueden tener la misma velocidad. [Ball] A siempre irá a 10 mph, y B a 15 mph. Pero cuando están en [posición] 2, ¿cómo podrían encontrarse si no tienen la misma velocidad? ¿No lo harían, al menos en el instante en que se encontraron? Enfrentados con el mismo problema, otros dos estudiantes argumentaron, AL: "Desde que se conocieron... se encuentran durante un cierto período, sin importar cuán pequeño sea... durante ese período, están en la misma posición, deben tener la misma velocidad, de lo contrario, ¿cómo podrían haberse conocido?" SC: "Su velocidad sería de 13 mph más o menos... pero tienen velocidades constantes... B cubre una distancia más larga que A, pero ambos llegan allí [posición 2] en el mismo punto... y durante el mismo tiempo... ¡Oh, no! Deberían tener velocidades diferentes a 2". Enfrentados con el mismo problema, otros dos estudiantes argumentaron, AL: "Desde que se conocieron... se encuentran durante un cierto período, sin importar cuán pequeño sea... durante ese período, están en la misma posición, deben tener la misma velocidad, de lo contrario, ¿cómo podrían haberse conocido?" SC: "Su velocidad sería de 13 mph más o menos... pero tienen velocidades constantes... B cubre una distancia más larga que A, pero ambos llegan allí [posición 2] en el mismo punto ... y durante el mismo tiempo ... ¡Oh, no! Deberían tener velocidades diferentes a 2". El resto del protocolo para SC, que no relatamos, proporcionó un bello ejemplo de equilibrio intelectual, ya que reconoció una contradicción en su pensamiento y continuó, con alguna ayuda del entrevistador, para discriminar entre velocidades promedio e instantáneas. B. Movimiento libre de partículas Los estudiantes con creencias aristotélicas produjeron los argumentos más extraños. Así, un estudiante argumentó que el bloque X de la tarea (XI) se detendría instantáneamente después de que las fuerzas externas dejaran de conducirlo porque "se necesitan ruedas para mantenerlo funcionando". Los argumentos proporcionados por los pensadores ímpetu eran más plausibles. Los estudiantes GT y ST mostraron caminos derechos para que la pelota salga del tubo de la tarea (V). Sin embargo, tenían dos creencias erróneas típicas sobre el tipo de velocidad que tendría la bola a lo largo del camino: GT: "...la pelota antes quería ir en línea recta, pero como [el tubo] no la suelta, la pelota adquiere una potencia que hará que la pelota se sacuda [cuando abandone el tubo] y adquiera una nueva velocidad más grande que la que tenía antes... Esta potencia depende de cuánto tiempo gire la bola dentro del tubo... Permitirá que la bola se acelere hasta que se desgaste. Luego, la bola gira a velocidad constante". ST: [Cuando la bola se mueve dentro del tubo], "adquiere una potencia que espera ser liberada. La velocidad de rotación [dentro del tubo] crea una fuerza o una potencia... que hace que la bola primero se acelere, luego después la potencia desaparece, [la bola] comienza a desacelerarse".... La mayoría de los estudiantes de ímpetu creían que el ímpetu comienza a desgastarse en el instante en que la bola sale del tubo, mientras que otros sostienen que este ímpetu se mantiene hasta que se encuentra cierta resistencia. Para ese ímpetu, los estudiantes usaron los nombres potencia, fuerza, aceleración, velocidad, momento, inercia o energía indiscriminadamente. Otros dos estudiantes, AC y SC, habían mostrado trayectorias curvas para la bola de la tarea (V), y argumentaron que el movimiento se mantiene mediante una especie de ímpetu circular. AC: "Cuando entrena algo para hacer algo durante bastante tiempo... esta cosa [la pelota] hará lo mismo [moverse en un camino curvo] para lo que se entrenó a hacer". SC: "La pelota va así [camino curvado] porque todavía tenía algo de impulso cuando la estaba girando en un círculo, y quiere ir en línea recta, así que no va en círculo [de vuelta al interior del tubo] y no en una línea recta. En cambio, va [en una curva] hasta que el impulso se agote... luego va derecho". Un compromiso entre la "tendencia natural" de la pelota para ir derecho y el movimiento para el que fue entrenado fue compartido de manera diferente por menos del 1% de los estudiantes. Esos estudiantes argumentaron que, como resultado del movimiento circular dentro del tubo, la bola de la tarea (V) adquiere una tendencia a moverse radialmente hacia fuera, es decir, a abandonar el tubo en una dirección centrífuga. El camino real que sigue la bola fuera del tubo será un compromiso entre la tendencia centrífuga adquirida y su tendencia tangencial natural. Un estudiante que había mostrado un camino de compromiso en la prueba previa explicó: "La pelota sale en la dirección de la resultante de la aceleración de la rotación [la tendencia a moverse tangencialmente al tubo] y la fuerza centrífuga que tomaría la pelota [radialmente hacia afuera]". Incidentalmente, el mismo estudiante había argumentado que si la bola de la tarea (V) dejaba un tubo suspendido en el aire, pero en ausencia de gravedad, la bola "permanecería en su lugar. No se movería más allá del punto donde la dejaste". "Sin embargo, cuando el tubo se coloca sobre una mesa horizontal, el movimiento lineal de la bola fuera del tubo es posible debido a la presencia de un soporte rígido o guía: la mesa. Por otro lado, el estudiante argumentó que el movimiento lineal en el aire fino también podría haber sido posible fuera del tubo, o más allá del borde de la mesa, si el tubo o la mesa en la que se apoya el tubo fueran "lo suficientemente largos como para... entrenar la pelota para ir por ese camino". El 28% de los estudiantes en tareas (IX) de la prueba preliminar mostró una especie de conservación de ímpetu. Esos estudiantes creían que en la etapa final del movimiento del cohete, después de que se apagaran los motores, el cohete volvería a la dirección de movimiento que tenía antes de encender los motores. Los estudiantes entrevistados que demostraron tal creencia argumentaron que cuando el cohete navegaba en el espacio en ausencia de fuerzas externas, estaba dotado de un tipo de ímpetu que lo llevaba en la dirección especificada. Cuando se encienden los motores, continuaron, una fuerza actúa en contra de ese ímpetu y toma el cohete en una dirección de compromiso. "Cuando apagas los motores", argumentó un estudiante, "solo hay una componente horizontal [la que es paralela a la dirección inicial] de la velocidad, y el cohete va en esa dirección". El trece por ciento de los estudiantes había argumentado que en la segunda etapa (cuando los motores están encendidos) el cohete adquiere un nuevo ímpetu que se suma al anterior en la etapa final. Como resultado, el cohete se mueve en la dirección de la resultante de los dos impulsos después de que los motores se apagan. Los estudiantes con creencias de Impétus difirieron no solo con respecto a cómo se mantienen la velocidad y la dirección del movimiento impresionado, sino también con respecto a cómo se adquiere un ímpetu, y si se disipa y cómo se disipa. Estas diferencias se revelan mejor en la Sec. IV C y D. C. Movimiento unidimensional bajo una fuerza constante En esta subsección examinamos las creencias de los estudiantes sobre el movimiento bajo una fuerza constante, incluyendo la caída gravitacional libre y la caída restringida a las pendientes. En la prueba preliminar, el 14% de los estudiantes compartía la creencia de que una partícula sujeta a una fuerza constante se mueve con una velocidad constante. De los estudiantes que sostienen que bajo una fuerza constante la velocidad de una partícula aumenta continuamente, el 40% cree que el aumento en la velocidad es proporcional a la magnitud de la fuerza y la distancia recorrida. De todos los estudiantes, el 47% cree que el intervalo de tiempo requerido para viajar una distancia específica bajo una fuerza constante es inversamente proporcional a la magnitud de la fuerza. Ninguno de los estudiantes mostró la creencia aristotélica de que una fuerza motriz constante mueve un objeto físico solo a una distancia limitada. Pero el 27% de los estudiantes sostuvo que una fuerza no puede seguir acelerando un objeto indefinidamente, y que el objeto alcanza un límite de velocidad crítico determinado por la magnitud de la fuerza y la masa del objeto. Con respecto a la tarea (XI), el alumno CM argumentó que "si la masa del bloque X es mayor que la fuerza de [tracción] de Y, el bloque X permanece en su lugar... no podría moverse". Para CM, como para Aristóteles, la masa de un objeto es una fuerza resistiva incluso en superficies sin fricción. Se preguntó a los estudiantes que compartieron esta creencia durante las entrevistas que imaginaran que el bloque X tiraba de diferentes superficies, por ejemplo, superficies de madera pulidas y sin pulir, arena, hielo, etc., y para comparar los movimientos que el bloque sufriría en las diversas superficies. CM, como algunos estudiantes más, sostuvo que la masa del bloque siempre resiste el movimiento de la misma manera, excepto en superficies como el hielo, pero solo porque "el hielo es resbaladizo". Los estudiantes que creían que una partícula bajo una fuerza constante siempre alcanzaba un límite de velocidad proporcionaban diversos argumentos para su creencia. GT: "El Bloque X primero acelera hasta que alcanza una velocidad igual al tirón de Y... luego continúa a esa velocidad... Esa velocidad máxima siempre es igual a la fuerza que apliques. [Por ejemplo, si aplique una fuerza de 10 lbs. Para el bloque X], la velocidad máxima sería igual a 10 pies / s. " BM: "Una fuerza constante acelera un cuerpo... pero solo hasta que el cuerpo alcance la velocidad que habría utilizado todo el poder de la fuerza. [El cuerpo luego se mueve a velocidad constante]". AP: "¿No hay un límite para todo?... ¿Cómo podría un objeto ir más y más rápido todo el tiempo ... debe haber un límite". PA: "La gravedad baja [de un objeto en caída libre], pero hay algo que lo hace nivelar. No sé lo que es. Simplemente no parece razonable que su velocidad pueda seguir aumentando indefinidamente". AL: "Galileo hizo el experimento [de caída libre] en Pisa y dijo que [los objetos que caen] alcanzan un límite de velocidad. Supongo... porque Galileo lo hizo, o al menos si lo que sé sobre él es cierto, esto debe ser cierto." KC: "Respondí que hay una velocidad máxima [en caída libre] porque basé mi respuesta en lo que un amigo me dijo. Es paracaidista. Me dijo que debido al aire, pueden alcanzar un límite de velocidad". Las dos últimas declaraciones nos recuerdan que los estudiantes están demasiado preparados para justificar sus creencias apelando a la autoridad, uno de los logros de la enseñanza del conocimiento memorístico pasivo. Siete entrevistados creían que después de que el bloque X de la tarea (XI) alcance su velocidad máxima, esa velocidad se mantendrá si el bloque Y permanece conectado al bloque X. Además, algunos creen que cambiar la magnitud de la fuerza motriz no cambia la magnitud del límite de velocidad. Por ejemplo, GT argumentó que si "duplicas el tirón en el bloque X [la velocidad máxima] permanece igual, solo el tiempo ... y la distancia ... para alcanzar ese máximo se reducirán a la mitad". Seis estudiantes entrevistados que habían argumentado a favor de una velocidad máxima en caída libre dijeron que esta velocidad "es igual a la gravedad ... 32 pies / s". Por otro lado, algunos estudiantes creían que "la gravedad no actúa instantáneamente desde el momento en que [establece un objeto libre para caer], lleva un tiempo". JS y CM presentaron argumentos similares: JS: "La fuerza cero actúa sobre la bola [en el instante en que se lanza]. A medida que baja, la fuerza de la gravedad aumenta... y es por eso que la velocidad aumenta". CM: [Una bola que cae libremente] "va cada vez más rápido porque la gravedad tira más y más a medida que desciende. Es como un imán. Cuanto más cerca esté el objeto del imán, más difícil será atraído... La gravedad tira más fuerte , cuanto más se acerca la pelota a la tierra ". Por otro lado, algunos estudiantes creen que la gravedad no actúa de la misma manera en una caída libre y limitada. La distinción, sin embargo, no está clara. Algunos estudiantes, como PD, creen que en caída libre, pero no en pendientes, los objetos se mueven con la misma aceleración independientemente de sus propiedades físicas. PD: "Los cuerpos más pesados se deslizan por una pendiente más rápido que los más livianos... incluso si se ignoran la fricción y la resistencia del aire... En las pendientes, la gravedad no actúa igual [en caída libre]... de alguna manera hay una diferencia, pero no sé lo que es". Para algunos estudiantes, la gravedad se manifiesta por una fuerza constante pero no por una aceleración constante. Objetos de diferente masa no pueden caer con la misma aceleración. CM: "Gravedad significa la misma fuerza en cualquier objeto... tira tan fuerte... de la misma manera... quiero decir con la misma fuerza en todos los objetos". PM: "La gravedad significa que la misma fuerza tira de diferentes objetos... Sé que la gravedad es 9.8 para todos los cuerpos". JM: "La aceleración de la gravedad es constante. Luego, si duplicas la masa... y dado que tienes la misma aceleración... dos unidades de masa van a la mitad de una unidad de masa". Algunos estudiantes incluso creyeron que el peso y la "gravedad" son dos fuerzas diferentes. KB argumentó que "la velocidad [de caída libre] se debe al peso y la gravedad se debe a la resultante de ambos". Para estudiantes como KB, el peso aumenta con la masa de un objeto que cae, mientras que la "gravedad es constante para todos". O, otro estudiante dice, PA: "Los objetos más pesados caen más rápido porque sé esto... porque tenemos dos niños... y cuando bajamos por un tobogán de agua que es razonablemente sin fricción... voy más rápido cuando tengo un niño sobre mis hombros que cuando bajo solo... La gravedad es la misma para todos los objetos... Es lo mismo tirar por todos lados para diferentes objetos... Pero al lado de la gravedad está el peso... [Sin embargo, si dos objetos de diferentes masas caen juntos], el más pesado cae más rápido primero hasta cierto punto... luego el otro alcanza y se nivela... y van juntos a la misma velocidad el resto del tiempo". Este proceso de "recuperación" se revela mejor en la Sec. IV D. En cuanto a por qué sucede, los estudiantes no pudieron dar una explicación mejor que "Sé que simplemente sucede" o "parece lógico". D. Movimiento bidimensional bajo una fuerza constante Muchos estudiantes tienen alguna noción de movimiento parabólico, pero pocos de ellos lo reconocen como la consecuencia de una fuerza constante. Así, el 66% de los estudiantes previamente probados pudieron identificar la ruta parabólica correcta para el proyectil de la tarea (VI), pero solo el 20% de esos estudiantes pudieron identificar el camino similar para el cohete disparando sus motores en la tarea (IX). Las entrevistas confirmaron que los estudiantes tenían grandes dificultades para identificar un principio común en las dos tareas. Fig. 2. Trayectorias de proyectiles dependiendo de cómo se impartió un ímpetu: (a) para un objeto lanzado a mano, (b) para un objeto lanzado desde un avión y (c) para un objeto proyectado fuera de una mesa. La mayoría de los estudiantes mantienen conceptos de impulso, pero las diferencias en sus conceptos son evidentes en sus comentarios sobre el movimiento del proyectil. Algunos de ellos creen que el movimiento de un proyectil no solo está determinado por su velocidad inicial, sino también por cómo se impartió esa velocidad. JT afirmó que una pelota lanzada en el aire con una velocidad inicial v va horizontalmente por un tiempo, viajando una distancia que es mayor si la pelota es lanzada a mano, más pequeña si es lanzada desde un avión que vuela a esa velocidad, y mucho más pequeña si se proyecta fuera de una mesa con velocidad v (Fig. 2). Otro estudiante que abogó por los mismos caminos trató de explicar la diferencia. AC: "[En caso (a)] le estás dando al balón una velocidad en una dirección recta... mientras más fuerte lo arrojes, más irá recto. [En los casos (b) y (c)] no estás dándole potencia, no le diste a la pelota potencia para ir en línea recta primero como lo hiciste [en el caso (a)]. Aquí, [caso (a)] le estás dando una energía, una cierta energía para que siga recto... allí, porque el avión simplemente lo estaba cargando [y porque la mesa estaba dirigiendo el balón]... el avión no le da [a la pelota] una potencia para ir derecho". Los estudiantes RS y DL argumentaron que la pelota de la Fig. 2 va como se muestra en los casos (a) y (c), pero no en el caso (b). En el último caso, la bola iría directamente en ángulo con la horizontal, como se muestra en la Fig. 3. DL: [El camino seguido por la pelota] "es la resultante de la velocidad que le dan el avión y la gravedad ... [pero si los motores del avión se apagan repentinamente, o la pelota se lanza a mano o se proyecta desde una tabla] el avión / bola es así [Fig. 2 (a)] porque la velocidad horizontal supera la gravedad ... la fuerza horizontal que es un producto del estallido ... es mayor que la gravedad ... aquí [cuando el la bola se suelta del avión volador] esta bola se acaba de caer ... primero fue transportada por el avión y se acaba de caer. No se le da ninguna explosión ni nada ". AL: [Argumentó que un proyectil cae directamente a menos que se lance con una velocidad cuya magnitud está por encima de un cierto nivel crítico, sin importar desde qué ángulo se lance ese proyectil. Además, argumentó que no importa cómo se lance un proyectil, nunca comienza su movimiento de manera tangencial a la velocidad inicial, y eso es "porque la gravedad lo está derribando". Fig. 3. Velocidad de "compromiso" vy trayectoria de un proyectil liberado con velocidad inicial u sujeto a "gravedad g". Algunos estudiantes, como RS, argumentaron que el proyectil podría comenzar el movimiento en la dirección de la velocidad inicial, pero solo si esa velocidad es "mayor que la gravedad" (Fig. 4). Fig. 4. Camino de un proyectil sujeto a "gravedad g" y liberado con velocidad inicial u. (a) "menor que o igual a g", o (b) "mayor que g". Los estudiantes que argumentaron a favor de los caminos de la Fig. 2 se dividieron en cuanto a cómo varía el ímpetu. Algunos, como RS, mantuvieron que el ímpetu, de ahí la velocidad del proyectil impreso, permanece constante a lo largo de la parte horizontal del camino. Otros, como JS, sostuvieron que el ímpetu comienza a desgastarse desde el instante en que un proyectil impresionado se desconecta del motor original. En consecuencia, la velocidad del proyectil disminuye a lo largo de la parte recta del camino que está en la dirección de la velocidad inicial. RS: "Su velocidad permanece constante... debido a la potencia... debido a la fuerza detrás de ella... hasta que la potencia comienza a desgastarse... y la velocidad inicial es superada por la gravedad. Entonces [la bola comienza a curvarse y] su velocidad sigue aumentando a causa de g ... Sigue curvando hasta que la potencia desaparece [o como lo pone AL, "hasta que la velocidad horizontal se vuelve cero"]... luego la gravedad toma el control... y la bola cae recta abajo a velocidad constante ". JS: "La pelota va primero en línea recta debido a la fuerza detrás de ella... Esta fuerza es constante ... ¡Oh, no! No puede ser, porque se ralentiza aquí [a lo largo de la parte horizontal del camino] La fuerza, entonces, debe disminuir hasta aquí [donde comienza la curvatura], porque la gravedad actúa sobre ella... de aquí en adelante [la parte vertical recta del camino] no hay más fuerza detrás de ella... solo la gravedad la atrae abajo." Algunos estudiantes, como SL, mantuvieron que el ímpetu permanece constante, o como TS, que el ímpetu puede acumularse durante el movimiento. SL: "Debido a la cantidad de energía o fuerza con la que lo disparas a... el empuje del disparo hace que la bola siga en línea recta... Pero la gravedad tira de la bola ... tira cada vez más. ... hasta que [la gravedad] es igual a esta cantidad de fuerza [ímpetu]. La bola comienza a curvarse hacia abajo... sigue curvando debido a la cantidad de energía que todavía la impulsa hacia adelante... pero la gravedad se está volviendo cada vez más grande" TS: "La fuerza [ímpetu] aumenta a medida que la pelota cae, porque la gravedad está empujando hacia abajo ahora en la misma dirección del movimiento... luego proporciona a la pelota más y más fuerza a medida que desciende... pero la gravedad, la atracción de la gravedad es constante". Se dieron argumentos similares a los anteriores para los proyectiles lanzados en ángulo con la horizontal (Fig. 5). Fig. 5. Rutas de impulso típicas para proyectiles lanzados en una dirección oblicua JT: [En el camino hacia arriba], "la pelota va hacia arriba debido a la fuerza ... que la pelota recibe cuando la disparas ... Esta fuerza disminuye en el camino hacia arriba ... pero la pelota se mueve a velocidad constante ... La fuerza no tiene nada que ver con la velocidad, solo tiene que mantener la bola en movimiento ... [En el camino de descenso] ya no necesitas esa fuerza ... La pelota se caería, me refiero siempre cae si no hay fuerza, entonces debe haber una fuerza que mueva la bola hacia arriba, pero esta fuerza no puede permanecer igual porque la bola quiere bajar ... y esto toma un poder de la fuerza, por lo que disminuye [a un valor que no es grande] lo suficiente como para llevar la pelota hacia arriba ... pero lo suficiente como para llevarla hacia un lado en lugar de [caer directamente] ". Para JT, esa bola mantiene una velocidad constante durante todo su movimiento. RS: [Alrededor de la trayectoria (c) de la Fig. 5], "la fuerza detrás de ella disminuye ... pero no completamente ... La bola cae a velocidad constante ... la potencia inicial tiende a tomar la bola [horizontalmente] pero la gravedad tira hacia abajo [verticalmente] de modo que el camino [en el camino hacia abajo] es la resultante de ambos [ímpetu y gravedad]. Para la mayoría de los estudiantes, un ímpetu mantiene el movimiento en la dirección de la velocidad de proyección o en la dirección de la resultante de esa velocidad y otras fuerzas existentes. Sin embargo, para el 15% de los estudiantes, un ímpetu también mantiene la trayectoria del movimiento, como si un objeto impresionado "entrenado para hacer algo" se dota de un recuerdo, o se condiciona "a hacer lo que está capacitado para hacer". V. UNA TAXONOMÍA DE CONCEPTOS DE SENTIDO COMÚN SOBRE EL MOVIMIENTO Para organizar nuestro conocimiento sobre los conceptos de CS y proporcionar una guía para aplicarlo a la instrucción, en esta sección desarrollamos una breve taxonomía comentada de los conceptos CS más significativos. Sería poco práctico categorizar las muchas variaciones de cada concepto que se encuentra entre los estudiantes, por lo que hemos intentado dar formulaciones de los conceptos que expresan las creencias más comunes. Para desarrollar una taxonomía, necesitamos principios de clasificación. Afortunadamente, la mecánica newtoniana nos proporciona un esquema de clasificación ya preparado, y podemos clasificar los conceptos de CS sobre el movimiento como alternativas a los conceptos newtonianos específicos. En consecuencia, reconocemos dos categorías generales: principios de movimiento, que corresponden a las Leyes del movimiento de Newton e influencias sobre el movimiento, que corresponden a leyes de fuerza específicas en la mecánica newtoniana. A. Principios del movimiento (1) Descripción del movimiento: los conceptos cinemáticos CS comúnmente tienen las siguientes características. (a) Los conceptos de "intervalo de tiempo" e "instante de tiempo" no se diferencian. Un "instante" se considera como un intervalo de tiempo muy corto. (b) La velocidad se define como la distancia dividida por el tiempo. Por lo tanto, la velocidad promedio no se diferencia de la velocidad instantánea. (c) Los conceptos de distancia, velocidad y aceleración no están bien diferenciados. (2) En ausencia de fuerzas, cada objeto permanece en reposo (con respecto a la tierra). En un sistema de sentido común, este principio juega un papel análogo a la Primera Ley de Newton. La adopción tácita de la tierra como un marco de referencia preferido es especialmente significativa, ya que indudablemente se basa en la experiencia perceptiva directa. Una de las maravillas del sistema perceptivo humano es el hecho de que a partir de diversos aportes sensoriales crea una representación de un ambiente en reposo mientras el sujeto observador se mueve, en lugar de uno en el que el observador está siempre en reposo mientras el entorno se mueve. Por supuesto, no se puede negar el testimonio de los sentidos, sino que la teoría newtoniana nos dice cómo se debe reinterpretar para que sea consistente con un rango más amplio de experiencia. Este ejemplo sugiere que para tratar de manera más efectiva con creencias particulares de CS, el diseño de instrucción debe depender de cómo esas creencias se basan en la percepción, pero ese es un asunto para futuras investigaciones. (3) El principio causal del movimiento: cada movimiento tiene una causa. Este es un análogo CS de la segunda ley de Newton. (a) El movimiento se inicia con (i) una fuerza aplicada al objeto por un agente externo; (ii) Gravedad, una tendencia intrínseca a caerse. (b) El movimiento es sostenido por (i) acción continua de una fuerza o gravedad aplicada, (ii) una fuerza interna (Impetus) en el objeto. (c) Movimiento puede ser opuesto por (i) resistencia intrínseca (peso o masa) del objeto, (ii) resistencia de un medio que rodea el objeto, (iii) obstáculos que "se interponen en el camino". La acción de un medio resistivo o un obstáculo no es una fuerza activa, porque no inicia ni sostiene el movimiento. Sin embargo, puede llamarse una fuerza reactiva para ayudar a los estudiantes a desarrollar un concepto de fuerza general. (4) La tercera ley de Newton es inconsistente con las intuiciones de sentido común. Maloney [17] ha estudiado y clasificado las reglas generadas por los estudiantes para tratar situaciones en las que se aplica la tercera ley. Descubrió que la mayoría de los estudiantes caracterizan la interacción recíproca entre dos objetos por algún tipo de principio de dominancia: (a) La masa mayor ejerce la fuerza mayor, o más frecuentemente, (b) el objeto que causa el movimiento del otro ejerce la fuerza mayor, porque supera la oposición del otro. (5) El principio de superposición newtoniano (Vector de suma de fuerzas) tiene dos análogos CS: (a) Dominación: el movimiento está determinado por la mayor de dos fuerzas competidoras. Este principio tiene un origen natural en la experiencia de que, para mover un objeto pesado, uno tiene que empujar más y más duro hasta que el empuje "supera" la resistencia, y se necesita menos esfuerzo para mantener el movimiento. Un estudiante necesita reinterpretar esta experiencia para aceptar la teoría newtoniana. Las declaraciones de los libros de texto, como "la resistencia se puede descuidar", podrían ser interpretadas por los estudiantes como la confirmación del principio de dominación. (b) Compromiso: la moción se determina mediante un compromiso entre fuerzas competidoras. Por supuesto, el principio de superposición puede considerarse como una especie de compromiso, pero las ideas de compromiso de los estudiantes probablemente sean vagas o impliquen un ímpetu. A veces, los principios de dominancia y compromiso se usan juntos, como vimos en relación con la figura 4. B. Influencias sobre el movimiento (1) Una fuerza aplicada es un empuje o tirón ejercido por un agente en contacto directo con el objeto. Para algunos, solo los seres vivos son reconocidos como agentes de la fuerza. El efecto de una fuerza aplicada se caracteriza comúnmente por los siguientes principios causales: (a) Resistencia inercial: una fuerza no puede mover un objeto a menos que sea mayor que el peso del objeto. El peso no se distingue de la masa. (b) Una fuerza constante produce una velocidad constante, a veces expresada como F = mv. (c) La aceleración se debe al aumento de la fuerza. (d) Una fuerza constante tiene un efecto limitado dependiendo de su magnitud. La limitación puede ser de dos tipos: (i) La fuerza se desgasta, debido a su consumo por el movimiento o su disipación por agentes resistivos. Además, su efecto puede no ser instantáneo, en el sentido de que el efecto puede no comenzar hasta algún momento después de que se aplica la fuerza. (ii) La fuerza F acelera el objeto hasta que alcanza una velocidad crítica proporcional a F, que el objeto mantiene luego si la fuerza todavía se aplica o no. (e) Una fuerza de largo alcance debe ser transmitida por un medio, como un objeto y agente de conexión de cuerda. Por lo tanto, las fuerzas de largo alcance no pueden actuar sobre un objeto en el vacío. (2) Una fuerza interna (o ímpetu) mantiene el movimiento de un objeto independiente de agentes externos. Como ha observado Clement2, según este principio, los estudiantes frecuentemente infieren la existencia de una fuerza en la dirección del movimiento de un objeto. (a) Un impulso puede ser impartido por una fuerza aplicada y transmitirse de un objeto a otro. (b) El ímpetu de un objeto es proporcional a su masa y velocidad, como lo expresa la ecuación F = mv. (c) Un ímpetu puede desgastarse o acumularse de la misma manera que el efecto de una fuerza aplicada. (3) La resistencia se opone a una fuerza aplicada o consume el ímpetu de un objeto en movimiento. Los siguientes tipos de resistencia no siempre se distinguen: (a) La inercia (peso o masa) es una resistencia intrínseca de un objeto al movimiento. (b) Fricción debido al contacto con una superficie sólida. (b) La resistencia del fluido depende de la densidad del fluido, así como del tamaño, forma y peso del objeto. (4) Los obstáculos pueden redirigir o detener el movimiento, pero no pueden ser agentes de una fuerza aplicada. Minstrell5 ha analizado los conceptos de los estudiantes de las fuerzas reactivas. (5) La gravedad es una tendencia de los objetos a caerse. En esta concepción, la gravedad no es necesariamente una fuerza. Sin embargo, los principios causales de las fuerzas aplicadas que señalamos anteriormente pueden atribuirse también a la gravedad. Como vimos en nuestra discusión de la física aristotélica, una consecuencia importante de esos principios es la creencia de que los objetos más pesados caen más rápido. Esta creencia es tan común que merece ser examinada cuidadosamente en las clases de física. En las secciones anteriores notamos otras creencias sobre la gravedad, y Gunstone y White observan más.6 Pero más importante que las creencias particulares sobre la gravedad puede ser la incertidumbre de los estudiantes sobre lo que "realmente es la gravedad". Entonces, la mejor estrategia de enseñanza puede ser la directa que persiga convencer a los estudiantes de que la gravedad es una fuerza, en particular una fuerza de largo alcance. La idea de una fuerza de largo alcance es difícil de entender para los estudiantes y, como lo fue para muchos intelectos grandiosos en la historia. Históricamente, el estudio de los imanes de Gilbert fue lo más importante para convencer a la gente de la realidad de las fuerzas de largo alcance. Los instructores de Física pueden extraer una lección pedagógica de esto.