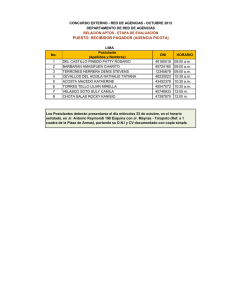
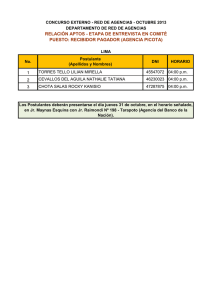
EJEMPLO EJERCICIO DE MAXIMIZACIÓN PROGRAMACION LINEAL Doña María trabaja en un negocio de comercio de conservas y maneja dos promociones: La promoción A consta de 1 carabela, 1 Mirella, y genera una utilidad de 50 soles; la promoción B consta de 2 carabela y 1 Mirella, y genera una utilidad de 80 soles. Diariamente cuenta con 120 carabela y 90 Mirella. ¿Cuántas promociones de cada tipo debe vender para generar la mayor utilidad? Recursos Carabela Mirella Utilidad Productos o servicios 1 2 1 1 50 80 Recursos disponibles 120 90 Definir las variables: X1= Cantidad de promociones A, a vender diariamente X2= Cantidad de promociones B, a vender diariamente Formular la función Objetiva: La función objetivo es maximizar la utilidad generada por las promociones. Dado que cada promoción A genera una utilidad de 50 soles y cada promoción B genera una utilidad de 80 soles, la función objetivo se puede expresar como. Maximizar: Z=50 x1 + 80 x2 Restricciones: Las restricciones están dadas por las cantidades limitadas de carabela y Mirella. Restricción de carabelas Cada promoción A usa 1 carabela y cada promoción B usa 2 carabelas. Doña María dispone de 120 carabelas. 1 x1 + 2 x2 ≤120 Restricción de Mirella Cada promoción A usa 1 Mirella y cada promoción B usa 1 Mirella. Doña María dispone de 90 Mirella. 1 x1 + 1 x2 ≤90 Restricciones de no negatividad: Las cantidades de promociones vendidas no pueden ser negativas. x1, x2 ≥0