Transformada de Laplace
CÁLCULO II
Departamento de Matemática Aplicada II
E.E. Telecomunicación
Definición Propiedades de la Transformada de Laplace La función Delta de Dirac Aplicación a las Ecuaciones Diferenciales Observaciones sobre la nota
Table of contents
1
Definición
2
Propiedades de la Transformada de Laplace
3
La función Delta de Dirac
4
Aplicación a las Ecuaciones Diferenciales
5
Observaciones sobre la notación
6
Ejercicios propuestos
Definición Propiedades de la Transformada de Laplace La función Delta de Dirac Aplicación a las Ecuaciones Diferenciales Observaciones sobre la nota
Definición
Se llama Transformada de Laplace de la función f (t), t ≥ 0, a la función
Z ∞
L {f (t)} = F (s) =
e−st f (t)dt ,
0
siempre y cuando la función esté definida.
Ejemplo. Sea f (t) = eat , entonces
L {f (t)} = L {e } =
at
Z ∞
∞
e−st eat dt =
0
Por tanto,
1 (a−s)t
e
a−s
0
si a > s ⇒
1
(e∞ − e0 ) = ∞ ⇒ @ L {eat }
a−s
si a < s ⇒
1
−1
1
(e−∞ − e0 ) =
=
.
a−s
a−s
s−a
Es decir,
L {eat } =
1
s−a
/
s>a.
Definición Propiedades de la Transformada de Laplace La función Delta de Dirac Aplicación a las Ecuaciones Diferenciales Observaciones sobre la nota
Definición
Sea F (s) = L {f (t)}, llamaremos Transformada Inversa de Laplace,
L −1 {F (s)} = f (t).
Observación
La transformada de Laplace es una herramienta que permite resolver problemas de
valor inicial de manera más sencilla. La idea es reemplazar un problema de valor
inicial en el dominio del tiempo t por una ecuación algebraica en el dominio de s
(la frecuencia en análisis de circuitos).
Definición Propiedades de la Transformada de Laplace La función Delta de Dirac Aplicación a las Ecuaciones Diferenciales Observaciones sobre la nota
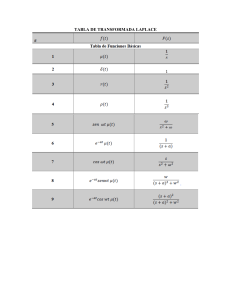
Algunas transformadas:
f (t)
L {f (t)} = F (s)
f (t)
L {f (t)} = F (s)
eat
1
s−a
k
k
s
t
1
s2
tn
n!
sn+1
sen(at)
a
s2 +a2
cos(at)
s
s2 +a2
senh(at)
a
s2 −a2
cosh(at)
s
s2 −a2
1
√
t
pπ
s
Definición Propiedades de la Transformada de Laplace La función Delta de Dirac Aplicación a las Ecuaciones Diferenciales Observaciones sobre la nota
Sean L {f (t)} = F (s), L {g(t)} = G(s) y α, β ∈ R. Entonces,
Linealidad
L {αf (t) + βg(t)} = αL {f (t)} + βL {g(t)}
L −1 {αF (s) + βG(s)} = αL −1 {F (s)} + βL −1 {G(s)}
Primera Traslación
L {eat f (t)} = F (s − a)
L −1 {F (s − a)} = eat f (t)
Segunda Traslación
g(t) =
f (t − a),
0,
L −1 {e−as F (s)} =
t>a
⇒ L {g(t)} = e−as F (s)
t<a
f (t − a),
0,
t>a
t<a
Definición Propiedades de la Transformada de Laplace La función Delta de Dirac Aplicación a las Ecuaciones Diferenciales Observaciones sobre la nota
Cambio de escala
L {f (at)} = a1 F
s
a
L −1 {F (as)} = a1 f
t
a
Transformada de las derivadas
L {f 0 (t)} = sF (s) − f (0)
L {f 00 (t)} = s2 F (s) − sf (0) − f 0 (0)
..
.
L {f (n (t)} = sn F (s) − sn−1 f (0) − . . . − sf (n−2 (0) − f (n−1 (0)
L {tn f (t)} = (−1)n F (n (s)
L −1 {F (n (s)} = (−1)n tn f (t)
Definición Propiedades de la Transformada de Laplace La función Delta de Dirac Aplicación a las Ecuaciones Diferenciales Observaciones sobre la nota
Transformada de las integrales
Rt
L { 0 f (x) dx} = F (s)
s
L −1 { F (s)
s }=
L { f (t)
t }=
Rt
R∞
s
0
f (x) dx
F (x) dx,
siempre que ∃ lı́mt→0 f (t)
t
R∞
L −1 { s F (x) dx} = f (t)
t
Teorema de Convolución
Rt
L { 0 f (x)g(t − x) dx} = F (s)G(s)
L −1 {F (s)G(s)} =
Rt
0
f (x)g(t − x) dx
Definición Propiedades de la Transformada de Laplace La función Delta de Dirac Aplicación a las Ecuaciones Diferenciales Observaciones sobre la nota
Ejemplo. Calcular L −1 { s23s+7
−2s−3 }
En primer lugar, se hace la descomposición en fracciones simples:
A
B
3s + 7
=
+
s2 − 2s − 3
s+1 s−3
⇒
A+B =3
⇒ A = −1,
−3A + B = 7
Aplicando las propiedades de linealidad:
−1
4
3s + 7
} = L −1 {
+
}=
L −1 { 2
s − 2s − 3
s+1 s−3
1
1
= −L −1 {
} + 4L −1 {
} = −e−t + 4e3t
s+1
s−3
B = 4,
Definición Propiedades de la Transformada de Laplace La función Delta de Dirac Aplicación a las Ecuaciones Diferenciales Observaciones sobre la nota
Ejemplo. Calcular L {e3t t2 }
Puede plantearse de dos formas:
Partiendo de que L {t2 } = s2!3 = s23 = F (s), utilizando la primera traslación
se obtiene
2
L {e3t t2 } = F (s − 3) =
.
(s − 3)3
1
Por otra parte, partiendo de L {e3t } = s−3
= F (s) , y teniendo en cuenta
que
2
−1
y F 00 (s) =
,
F 0 (s) =
(s − 3)2
(s − 3)3
se concluye que
L {e3t t2 } = (−1)2 F 00 (s) =
2
.
(s − 3)3
Definición Propiedades de la Transformada de Laplace La función Delta de Dirac Aplicación a las Ecuaciones Diferenciales Observaciones sobre la nota
Ejemplo. Calcular L { sen(t)
t }
Como lı́mt→0 sen(t)
= lı́mt→0 cos(t)
= 1, se tiene que
t
1
L{
sen(t)
}=
t
Z ∞
F (x) dx,
con F (s) = L {f (t)} = L {sen(t)} =
s
1
s2 + 1
Entonces,
sen(t)
L{
}=
t
Z ∞
s
∞
dx
π
= arctan(x) = − arctan(s) = arctan
x2 + 1
2
s
Ejemplo. Hallar L {h(t)}, siendo h(t) =
Rt
L {h(t)} = L {sen(2t)}L {cos(t)} =
0
1
s
sen(2x) cos(t − x) dx
2
s
s2 + 4 s2 + 1
=
2s
(s2 + 4)(s2 + 1)
Definición Propiedades de la Transformada de Laplace La función Delta de Dirac Aplicación a las Ecuaciones Diferenciales Observaciones sobre la nota
Delta de Dirac
Se llama Delta de Dirac, δ(t), al lı́mite lı́m f (t), donde
→0
1
, si 0 ≤ t ≤ f (t) =
0
si t > En algunos textos se conoce como “función” impulso (señal de amplitud infinita y
duración cero), pero no es una función sino una distribución que verifica:
Z ∞
δ(t − a)f (t)dt = f (a)
si f es continua y a ≥ 0
0
Utilizando esa propiedad, se prueba que la transformada de Laplace de δ(t) es:
L {δ(t)} = 1
Además, la “primitiva” de la Delta de Dirac es la función escalón.
Definición Propiedades de la Transformada de Laplace La función Delta de Dirac Aplicación a las Ecuaciones Diferenciales Observaciones sobre la nota
Aplicación a la resolución de EDOs
Sea una EDO de segundo orden lineal con coeficientes constantes
a0 y 00 + a1 y 0 + a2 y = f (t),
a0 6= 0
Aplicando la Transformada de Laplace a ambos lados, se convierte la EDO en una
ecuación algebraica, cuya solución viene dada por L {y(t)} = ys , de forma que la
solución de la ecuación diferencial será y(t) = L −1 {ys }
Ejemplo. Halla la solución del problema de valor inicial:
y 00 + y = t,
y(0) = 1,
y 0 (0) = −2
1
s2
1
1
1 + s2 (s − 2)
A Bs + C
s2 ys −s+2+ys = 2 ⇒ ys (s2 +1) = 2 +(s−2) =
= 2+ 2
2
2
s
s
s (s + 1)
s
s +1
1
s
3
con A = 1, B = 1, C = −3 ⇒ ys = 2 + 2
−
⇒
s
s + 1 s2 + 1
1
s
1
y(t) = L −1 { 2 } + L −1 { 2
} − 3L −1 { 2
} = t + cos(t) − 3 sen(t)
s
s +1
s +1
L {y 00 +y} = L {t} ⇒ L {y 00 }+L {y} = L {t} ⇒ s2 ys −sy(0)−y 0 (0)+ys =
Definición Propiedades de la Transformada de Laplace La función Delta de Dirac Aplicación a las Ecuaciones Diferenciales Observaciones sobre la nota
Ejemplo. Halla la solución del problema de valor inicial:
y 00 + y = cos(t),
y(0) = 0,
y 0 (0) = 1
L {y 00 } + L {y} = L {cos(t)} ⇒ s2 ys − sy(0) − y 0 (0) + ys =
ys (s2 + 1) − 1 =
s
s2 + 1
⇒ ys =
s2 + s + 1
2
(s2 + 1)
con A = 0, B = 1, C = 1, D = 0 ⇒ ys =
=
s
s2 + 1
As + B
Cs + D
+
2
s2 + 1
(s2 + 1)
1
s
+
⇒
s2 + 1 (s2 + 1)2
1
s
t
} + L −1 {
} = sen(t) + sen(t)
y(t) = L −1 { 2
2
2
s +1
2
(s + 1)
⇒
Definición Propiedades de la Transformada de Laplace La función Delta de Dirac Aplicación a las Ecuaciones Diferenciales Observaciones sobre la nota
Ejemplo. Halla la solución del problema de valor inicial:
y 00 − 4y 0 + 4y = t3 e2t ,
y(0) = 0,
y 0 (0) = 0
L {y 00 } − 4L {y 0 } + 4L {y} = L {t3 e2t } ⇒
3!
s2 ys − sy(0) − y 0 (0) − 4sys + 4y(0) + 4ys =
ys =
6
4
(s − 2) (s2 − 4s + 4)
y(t) = L −1 {
6
(s − 2)
=
6
(s − 2)
4 ⇒
(s − 2)
6 ⇒
1 5 2t
6 } = 20 t e
Definición Propiedades de la Transformada de Laplace La función Delta de Dirac Aplicación a las Ecuaciones Diferenciales Observaciones sobre la nota
Observaciones sobre la notación
En la asignatura Análisis de circuitos lineales, entre otras, se habla de la función
escalón unidad u(t) definida por :
1, si t ≥ 0
u(t) =
0
si t < 0
En nuestra notación, como nos restringimos a funciones definidas en el intervalo
[0, ∞), se corresponde con la función constante 1 y, por tanto, no aparece escrita
explicitamente. Por ejemplo, para t ≥ 0, k u(t) ≡ k,1 ≡ k.
Puede probarse que la “derivada” de la función escalón u(t) es la Delta de Dirac
δ(t) .
En cuanto al estudio de las fracciones simples cuando intervienen raı́ces complejas
conjugadas, es decir, de la forma:
F (s) =
As + B
α
β
As + B
=
=
+
2
2
(s − a) + b
(s − (a + bj))(s − (a − bj))
s − (a + bj) s − (a − bj)
Definición Propiedades de la Transformada de Laplace La función Delta de Dirac Aplicación a las Ecuaciones Diferenciales Observaciones sobre la nota
debe tenerse en cuenta que:
α=
A Aa + B
−
j,
2
2b
β=
A Aa + B
+
j = ᾱ
2
2b
Aa + B
A
yη=−
, es decir, α = γ + ηj, se tiene que la
Si denotamos γ =
2
2b
transformada inversa de Laplace del término es:
L −1 {F (s)} = Aeat cos(bt) +
Aa + B at
e sen(bt) = 2eat (γ cos(bt) − η sen(bt))
b
Si tenemos en cuenta que |α| =
p
cos(θ) =
γ 2 + η 2 , y elegimos θ tal que:
γ
,
|α|
sen(θ) =
η
|α|
la transformada inversa anterior puede escribirse también como:
L −1 {F (s)} = 2|α|eat cos(bt + θ)
Definición Propiedades de la Transformada de Laplace La función Delta de Dirac Aplicación a las Ecuaciones Diferenciales Observaciones sobre la nota
Ejercicios propuestos
1
Halla las Transformadas de Laplace de las siguientes funciones:
f (t) = t2 + 6t − 3
1
3
f (t) = 3e−4t + cos(5t) + t3 + 8
2
4
sen(t)
f (t) =
t
2
Halla las siguientes Transformadas Inversas de Laplace:
1
L −1 { 2
}
s + 6s + 13
6s
−
4
L −1 { 2
}
s − 4s + 20
3
Usando la Transformada de Laplace, resuelve
y 00 − 2y 0 + 5y = −8e−t , y(0) = 2 , y 0 (0) = 12
y 00 − 6y 0 + 13y = 2e3t cos(2t) , y(0) = 1 , y 0 (0) = 1
y 00 − y = 4et − 2e−t , y(0) = 1 , y 0 (0) = 4
y 00 − 2y 0 = 1 , y(0) = 2 , y 0 (0) = 1
4
1
. Calcula L −1 {F (s)} y deduce L −1 {F (5 (s)}
(s + 1)4
utilizando propiedades de la transformada de Laplace.
Sea F (s) =