MATEMATICAS BASICAS TEORIA 1

Matemáticas Básicas
UNIVERSIDAD PERUANA
CAYETANO HEREDIA
FACULTAD DE CIENCIAS E INGENIERÍA
DEPARTAMENTO ACADÉMICO DE CIENCIAS EXACTAS
MATEMÁTICAS BÁSICAS
TEORIA SEMANA 1
Números Reales
Aceptaremos la existencia de un conjunto llamado conjunto de números reales y denotado
por R. Los números reales se emplean en todas las áreas de la matemática y sus aplicaciones.
Sobre R se define una relación de igualdad que verifica las siguientes propiedades



Para todo 𝑎 ∈ ℝ se tiene 𝑎 = 𝑎. (Refleja)
Para todo 𝑎, 𝑏 ∈ ℝ si 𝑎 = 𝑏 entonces 𝑏 = 𝑎. (Simétrica)
Para todo 𝑎, 𝑏, 𝑐 ∈ ℝ si 𝑎 = 𝑏 𝑦 𝑏 = 𝑐 entonces 𝑎 = 𝑐. (Transitiva)
Además, el conjunto de los números reales es cerrado respecto a las operaciones de adición
o suma (denotada por +) y multiplicación o producto (denotada por ・). Esto significa que
dados dos números reales cualesquiera, la suma y la multiplicación de ellos es también un
número real. Estas operaciones satisfacen las siguientes propiedades, dados a, b y c números
reales arbitrarios, se verifican





Conmutatividad
𝑎 + 𝑏 = 𝑏 + 𝑎, 𝑎. 𝑏 = 𝑏. 𝑎
Asociatividad
𝑎 + (𝑏 + 𝑐) = (𝑎 + 𝑏) + 𝑐, 𝑎. (𝑏. 𝑐) = (𝑎. 𝑏). 𝑐
Elemento Neutro o Identidad 𝑎 + 0 = 𝑎, 𝑎. 1 = 𝑎
Elemento Inverso
𝑎 + (−𝑎) = 0, 𝑎. 𝑎−1 = 1 𝑠𝑖 𝑎 ≠ 0
Distributividad
𝑎. (𝑏 + 𝑐) = 𝑎. 𝑏 + 𝑎. 𝑐
Note que el cero (0) no tiene inverso multiplicativo ya que no existe un número que
multiplicado por cero dé uno.
A partir de la suma, se define la resta a − b = a + (−b).
De forma semejante, se define la división en términos de la multiplicación, para cualquier
número b ∈ R, b ≠ 0, 𝑎 ÷ 𝑏 = 𝑎/𝑏 = 𝑎 × 𝑏 −1
𝑎
1
Es común denotar la división por 𝑏, de donde, si b ≠ 0 tenemos b−1 = 𝑏.
A continuación, se listan algunas importantes propiedades válidas en los números reales. La
demostración de ellas, son consecuencia de los axiomas de cuerpo. Para a, b, c y d números
reales arbitrarios se verifican







𝑎. 0 = 0
𝑎 = 𝑏 𝑠𝑖 𝑦 𝑠ó𝑙𝑜 𝑠𝑖 𝑎 + 𝑐 = 𝑏 + 𝑐
𝑆𝑖 𝑐 ≠ 0, 𝑠𝑒 𝑡𝑖𝑒𝑛𝑒 𝑎 = 𝑏 𝑠𝑖 𝑦 𝑠ó𝑙𝑜 𝑠𝑖 𝑎. 𝑐 = 𝑏. 𝑐
𝑎. 𝑏 = 0 𝑠𝑖 𝑦 𝑠𝑜𝑙𝑜 𝑠𝑖 𝑎 = 0 𝑜 𝑏 = 0
−(−𝑎) = 𝑎
−(𝑎 + 𝑏) = −𝑎 − 𝑏
−(𝑎. 𝑏) = (−𝑎). 𝑏 = 𝑎. (−𝑏)
1
Matemáticas Básicas


𝑃𝑎𝑟𝑎 𝑎 ≠ 0 𝑠𝑒 𝑡𝑖𝑒𝑛𝑒 (𝑎−1 )−1 = 𝑎
𝑃𝑎𝑟𝑎 𝑎 ≠ 0, 𝑏 ≠ 0 𝑠𝑒 𝑡𝑖𝑒𝑛𝑒 (𝑎. 𝑏)−1 = 𝑎−1 . 𝑏 −1

𝑃𝑎𝑟𝑎 𝑏 ≠ 0, 𝑑 ≠ 0 𝑠𝑒 𝑡𝑖𝑒𝑛𝑒 𝑏 + 𝑑 = 𝑏𝑑 ,
𝑎 𝑐 𝑎. 𝑐
𝑦
. =
𝑏 𝑑 𝑏. 𝑑
𝑎 𝑐 𝑎. 𝑑
𝑆𝑖 𝑎𝑑𝑒𝑚á𝑠 𝑐 ≠ 0, 𝑒𝑛𝑡𝑜𝑛𝑐𝑒𝑠, ÷ =
𝑏 𝑑 𝑏. 𝑐
𝑎
𝑐
𝑎𝑑+𝑏𝑐
𝑎
𝑏
𝑐
−𝑑 =
𝑎𝑑−𝑏𝑐
𝑏𝑑
Conjunto ℕ = {1, 2, 3, ⋯ }, se denomina como conjunto de los números Naturales.
En algunas situaciones de la vida diaria, tales como:
▪ Determinar el número que sumado con 5, dé por resultado 2.
▪ Tener un sobregiro de $ 100 en una cuenta corriente.
▪ Disminuir la temperatura de 25 ºC a 20 ºC en un cierto instante de tiempo.
▪ Deber una cierta suma de dinero.
Nos encontramos con la dificultad de que no existen números naturales que puedan resolver
dichos problemas. Las soluciones se encuentran en un nuevo conjunto denominado conjunto
de los números Enteros 𝑍 = {⋯ , −3, −2, −1, 0, 1, 2, 3, ⋯ }, del alemán Zahl (número).
¿Existe algún número que multiplicado por 2 sea 1? En general, dados dos números enteros
m y n cualesquiera, ¿existe un número entero x que multiplicado por n (n ≠ 0) sea igual a m?
La respuesta negativa a estas preguntas obligó a los matemáticos a una ampliación del
conjunto, introduciendo un nuevo conjunto numérico denominado conjunto de los números
𝑝
racionales, denotado por y definido por: Q = {f / f = 𝑞 , p ∈ Z, q ∈ Z, q ≠ 0}, del inglés
Quotient (cociente).
Un número racional es aquel que puede expresarse como una fracción p q entre dos números
enteros: p (numerador) y q (denominador), con denominador q diferente de cero. Pero
también existen números que no pueden ser representados como una fracción, a este conjunto
lo denominamos I: conjunto de los números Irracionales. Tales números existen, por
ejemplo: √2, √3, e, 𝜋, etc.
Tanto los números racionales como los irracionales forman el conjunto de los números reales
ℝ = ℚ ∪ 𝐈. La siguiente figura muestra cómo se relacionan los conjuntos numéricos
mencionados:
2
Matemáticas Básicas
Recta de los números reales. Los números reales pueden ser representados por puntos en
una recta.
A cada punto sobre la recta le corresponde un número real único, y a cada número real le
corresponde un punto único en la recta.
El sistema de los números reales puede ser completamente descrito por un conjunto de
axiomas. Con estos axiomas podemos derivar todas las propiedades de los números reales
asociadas con las operaciones de suma, resta, multiplicación, y división, así como también
los conceptos algebraicos asociados con la factorización, la solución de ecuaciones y la
potenciación.
Ejemplo 1. Determinar y justificar Verdadero (V) o Falso (F).
a) 3𝑥(𝑥 + 5) = −5𝑥 −2 + 2
b) 5 − 𝑥 + 𝑦 2 = 5 + 𝑥 − 𝑦
𝑥
𝑥
𝑥
𝑥
c) 𝑥 − 2 + 3 = −𝑥 + 2 − 3
d) 2𝑥 − 5 + 𝑦𝑧 = 2𝑥 − 2 + 𝑧𝑥 − 3
Ejemplo 2. Operaciones con números reales.
1. Simplificar:
5
2
a) 7+ 1
5
3
b) 7
1
−
3 2/9
2 2/9
2. Simplificar:
𝑥
b) 9 − 9
a) 3[-2(3) + 6(2)]
e)
0
0
f) 0
7
𝑥
6
𝑦
7
c) 𝑦
d) 0
g)0 × 0
h) 2 − 4 + 6.
3
1
1
Observación
𝑓(𝑥) =
𝒙
𝒇(𝒙) =
𝟏
𝒙
1
, 𝑠𝑖 𝑥 ≠ 0
𝑥
−2
−1
−1/2
0
+1/2
+1
+2
−1/2
−1
−2
∄
+2
+1
+1/2
3
Matemáticas Básicas
Exponentes y radicales.
Para n entero positivo, xn es la abreviación del producto de n factores: x 3  x  x  x.
La letra n en xn se le denomina exponente y a x se le llama base.
Si n es un entero positivo tenemos:

𝑥 𝑛 = 𝑥. 𝑥. 𝑥 … . 𝑥
⃡𝑛 𝑓𝑎𝑐𝑡𝑜𝑟𝑒𝑠

𝑥 −𝑛 = 𝑥 𝑛 = 𝑥.𝑥.𝑥.…𝑥
1
1
⃡𝑛 𝑓𝑎𝑐𝑡𝑜𝑟𝑒𝑠


1
𝑥 −𝑛
𝟎
= 𝑥𝑛
𝒙 = 𝟏 𝒔𝒊 𝒙 ≠ 𝟎.
;
𝟎𝟎 𝒏𝒐 𝒆𝒔𝒕á 𝒅𝒆𝒇𝒊𝒏𝒊𝒅𝒐
Si r n = x donde n es un entero positivo, entonces r es una raíz n-ésima de x:
n
x.
Ejemplo 3.
32 = 9 y así 3 es una raíz segunda (raíz cuadrada) de 9.
a) Hallar el valor numérico de 𝑎2 + 𝑎𝑏 + 𝑏 2
si 𝑎 = 2 , 𝑏 = 3 .
b) Hallar el valor numérico de 18𝑎𝑏 + 72𝑎2 𝑏 2 − 6𝑎4 + 81𝑏 4 si 𝑎 = 1 , 𝑏 = 1⁄3
𝑛
La raíz n-ésima de x se denota mediante radical √𝑥 :
𝑛
√𝑥
𝑝𝑜𝑠𝑖𝑡𝑖𝑣𝑎 𝑠𝑖 𝑥 𝑒𝑠 𝑝𝑜𝑠𝑖𝑡𝑖𝑣𝑎
es {
}.
𝑛𝑒𝑔𝑎𝑡𝑖𝑣𝑎 𝑠𝑖 𝑥 𝑒𝑠 𝑛𝑒𝑔𝑎𝑡𝑖𝑣𝑎 𝑦 𝑛 𝑒𝑠 𝑖𝑚𝑝𝑎𝑟
4
Matemáticas Básicas
Ejemplo 4.
a)
3
3
1
b) √27
√−8
c) √−8
Si x es positivo, la expresión x p/q, donde p y q son enteros y q es positivo, se define
q
xp
A continuación, se enlistan las leyes básicas de los exponentes y radicales.
1.
x m  x n  x m n
3.
x n 
1
xn
1
 xn
n
x
xm
6.
1
xm
8. ( xy) n  x n y n
4.
xm
 x mn
n
x
( x m ) n  x mn
5.
7.
n
x
xn
9.    n
y
 y
11.
x1 / n  n x
13.
n
15.
m n
17.
m
x y 
n
x 0  1, x  0
2.
x
10.  
 y
n
 y
 
x
1
x 1 / n  n
x
12.
n
n
n
xy
x  mn x
14.
x
x
n
n y
y
16.
xm/n  n xm
x m  x.
Ejemplo 5. Realizar las operaciones respectivas para convertir TODOS los exponentes
positivos y simplificar.
8𝑎3 𝑏 −4
a) 𝐾1 = 2𝑎−5 𝑏5
𝑧 2 𝑦 7 𝑥 −3
b) 𝐾2 = √𝑥 4 𝑦 −3 𝑧 4
(8𝑠3 𝑡 3 )
2/3
c) 𝐾3 = (𝑠4 𝑡 −8 )1/4
Ejemplo 6. Realizar las operaciones respectivas para convertir TODOS los exponentes
positivos y simplificar.
𝑧𝑦 −2 𝑥𝑥 4
a) 𝐾1 = 𝑥 8 𝑦 3 𝑧 −4
𝑧 −2 𝑦 7 𝑥 −8
−4/3
b) 𝐾2 = ( 𝑥 4 𝑦 3 𝑧 4 )
5
Matemáticas Básicas
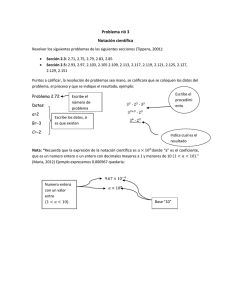
Notación científica.
Los científicos usan notación exponencial como una forma compacta de escribir números
muy grandes y números muy pequeños.
Por ejemplo, la estrella más cercana además del Sol, Proxima Centauri, está
aproximadamente a 40 000 000 000 000 de km de distancia.
La masa del átomo de hidrógeno es alrededor de 0,00000000000000000000000166 g.
Estos números son difíciles de leer y escribir, de modo que los científicos los expresan en
notación científica.
Para representar tales números se usa la notación científica en la forma:
𝑎 𝑥10𝑛
donde 1 ≤ 𝑎 < 10 y n toma un número entero.
Ejemplo 7. En notación científica escriba cada uno de los números siguientes.
a) 56 920
b) 0.000093
6