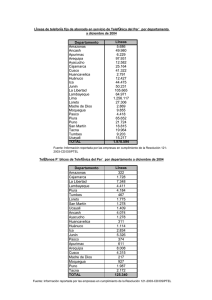
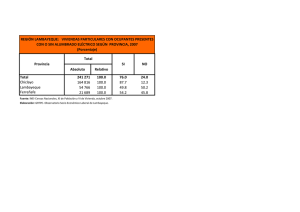
Prueba de entrada (2021 - 2) Pregunta 1: (Distribución binomial) De todas las flores plantadas por una empresa de jardinería, el 85% sobrevive. Si se plantan 15 flores ¿Cuál es la probabilidad de que 12 o más sobrevivan? Pregunta 2: (Distribución exponencial) El tiempo que transcurre antes de que una persona sea atendida en una cafetería es una variable aleatoria que sigue una distribución exponencial con media de 5 minutos. ¡Cuál es la probabilidad de que una persona sea atendida antes de que transcurran 4 minutos? Pregunta 3: (Distribución poisson) Un corredor de bolsa adquiere 80 acciones diferentes, concertando con sus clientes una ganancia de 1200 euros por acción. Por experiencias anteriores, se sabe que los beneficios de cada acción son independientes y se distribuyen uniformemente en el intervalo [1000, 2000]. ¿Qué probabilidad tiene el corredor de no perder dinero? Pregunta 4: Problema de Transporte. Una empresa energética del Perú dispone de cuatro plantas de generación para satisfacer la demanda diaria eléctrica en cuatro ciudades, La Oroya, Ancash, Lambayeque, y Huancavelica. Las plantas 1,2,3 y 4 pueden satisfacer 80, 30, 60 y 45 millones de KW al día respectivamente. Las necesidades de las ciudades de La Oroya, Ancash, Lambayeque y Huancavelica son de 70, 40, 70 y 35 millones de Kw., al día respectivamente. Los costos asociados al envío de suministro energético por cada millón de KW entre cada planta y cada ciudad son los registrados en la siguiente tabla. Planta 1 Planta 2 Planta 3 Planta 4 La Oroya 5 3 6 4 Ancash 2 6 1 3 Lambayeque Huancavelica 7 3 6 1 2 4 6 6 Formule un modelo de programación lineal que permita satisfacer las necesidades de todas las ciudades al tiempo que minimice los costos asociados al transporte.