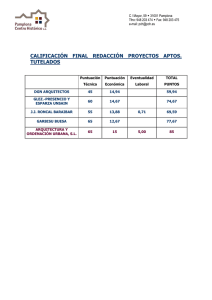
3. La información siguiente es un subconjunto de datos obtenidos en un experimento para estudiar la relación entre el Ph del suelo x y y A 1 La concentración /EC Root Responses of Three Gramineae Species to Soil Acidity in an Oxisol and and Ultisol Soil Science 1973 295 302. a. ¿Cuál es la función de regresión estimada para el modelo? b. Usando el modelo ajustado, ¿qué valor de y se pronosticaría cuando el pH del suelo es de 4.5 con intervalos de confianza y predicción al 95%? X Y 4,01 1,2 4,07 0,78 4,08 0,83 4,1 0,98 4,18 0,65 4,2 0,76 4,23 0,4 4,27 0,45 4,3 0,39 4,41 0,3 4,45 0,2 4.50 0,24 4,58 0,1 4,68 0,13 4,7 0,07 4,77 0,04 # REGRESION POLINOMICA #pH pH<- read.table("C:\Users\admin\Documents\pH.txt", header=TRUE) #GRAFICO EXPLORATORIO pH <- read.table ("pH.txt", header =TRUE) head(pH) attach(pH) plot(y ~ x, data= pH, col= "blue", pch= 19) # AJUSTE ANALITICO DEL MODELO ## polinomio impar no aumenta en R2 m2 <- lm(y ~ poly(x, 2), data=pH) #polinomio de grados #ir cambiando hasta que se ajuste idealmente summary(m2) > summary(m2) Call: lm(formula = y ~ poly(x, 2), data = pH) Residuals: Min 1Q Median 3Q Max -0.15463 -0.03791 -0.01087 0.05565 0.14327 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 0.47000 0.02333 20.145 3.47e-11 *** poly(x, 2)1 -1.27440 0.09332 -13.656 4.37e-09 *** poly(x, 2)2 0.40211 0.09332 4.309 0.000849 *** --Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 0.09332 on 13 degrees of freedom Multiple R-squared: 0.9404, Adjusted R-squared: 0.9312 F-statistic: 102.5 on 2 and 13 DF, p-value: 1.096e-08 Significancia del coeficiente P p-value: 1.096e-08 Si el valor P es < 0, 05 significa que el coeficiente es estadísticamente significativo, por lo que podemos qe nuestro p valor es muy significativo para explicar la relación entre el pH y la concentración. Error estándar residual: Este valor es 0,09332. Es una medida de qué tan lejos, en promedio, están las predicciones de los valores reales. Un error pequeño indica que el modelo ajusta bastante bien los datos, como se puede evidenciar en nuestro ejemplo. R ajustado es 0.9404: lo que significa que el 94.04% de la variación en la concentración se explica por el modelo es decir indica que el modelo está haciendo un buen trabajo al predecir los valores de concentración basados en el pH. # AJUSTE grafico DEL MODELO pred6 <- predict(m2) ## prediccion de los datos de etanol pred6 <- as.vector(pred6) ## convertir en vector i = order(x) ## ordenamos de forma creciente plot(y ~ x, col= "blue", pch = 19) lines(pred6[i] ~ x[i], col= "red", lwd = 3) #ajuste grafico del modelo #ANALISIS DE LOS RESIDUOS # NORMALIDAD require(car) qqPlot(m2$residuals, pch=20, ylab="Residuos", xlab= "Cuantiles normales", main="QQplot para residuos del modelo") # HOMOCEDASICIDAD E INDEPENDENCIA res <- as.vector(m2$residuals) plot(res~pred6, xlab="Valores ajustados", ylab="Residuos") ##PREDICE VALORES AJUSTADOS DEL MODELO abline(h=0, col="red", lwd=3) # PREDICCIÓN DE DATOS NUEVOS CON INTERVALOS DE CONFIANZA Y PREDICCIÓN newpH <- c(4.5) predict(m2, newdata = data.frame(x = newpH), interval = "confidence", level = 0.95) predict(m2, newdata = data.frame(x = newpH), interval = "prediction", level = 0.95) fit lwr upr 1 0.1670726 0.09016821 0.2439769 fit lwr upr 1 0.1670726 -0.04870549 0.3828506 Esto indica que, para un pH de 4.5, el modelo predice un valor promedio de y aproximadamente 0.167 con un intervalo de confianza del 95% que va desde 0.090 hasta 0.244.