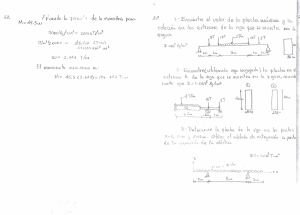
W ≔ 100 kip Viga W14x90 lbf Wp ≔ 90 ―― ft in V0 ≔ 18 ― s l ≔ 20 ft x0 ≔ 0 in I ≔ 999 in 4 E ≔ 29000 ksi Para el calculo de la rigidez a flexion de la viga el peso propio se puntualizara en el centro del claro, por lo tanto se sumara a la masa del bloque como una sola carga puntual. Por lo tanto: P ≔ W + Wp ⋅ l = 101.8 kip La deflexion maxima para viga con sus extremos empotrados y una carga puntual en el centro del claro es: P ⋅ l3 Δ = ――― 192 EI Sabemos que: F=K ⋅ Δ P K = ――― P ⋅ l3 ――― 192 E ⋅ I F=P 192 E ⋅ I K = ――― l3 192 E ⋅ I kip = 4828.5 K ≔ ――― ―― ft l3 Propiedades dinamicas Frecuencia natural w≔ ‾‾‾‾ K⋅g rad ――= 39.0648 ―― P s Periodo natural 2π = 0.1608 s T ≔ ―― w Frecuencia 1 1 f ≔ ―= 6.2173 ― T s ⎛ ⎛ V0 + ξxw ⎞ ⎞ x ((t)) = e -ξwt ⎜x0 ⋅ cos ((w ⋅ t)) + ⎜―――⎟ ⋅ sin ((w ⋅ t))⎟ w ⎝ ⎝ ⎠ ⎠ Como el desplazamiento inicial es cero y no hay amortiguamiento: x0 ⋅ cos ((w ⋅ t)) = 0 e -ξwt = 1 ⎛ V0 ⎞ x ((t)) ≔ ⎜―⎟ ⋅ sin ((w ⋅ t)) ⎝w⎠ El desplazamiento maximo se dara cuando: ⎛π⎞ sen ⎛⎝w ⋅ txmax⎞⎠ = sin ⎜―⎟ ⎝2⎠ π w ⋅ t = ―rad 2 π ― 2 txmax ≔ ―= 0.0402 s w Tambien se puede calcular como: T txmax ≔ ―= 0.0402 s 4 La maxima respuesta x ⎛⎝txmax⎞⎠ = 0.461 in ⎛ V0 ⎞ x ((t)) = ⎜―⎟ ⋅ sin ((w ⋅ t)) ⎝w⎠ t ≔ 0 s , 0.01 s ‥ 2 s 0.54 0.45 0.36 0.27 0.18 0.09 0 -0.09 0 0.2 0.4 0.6 0.8 1 -0.18 -0.27 -0.36 -0.45 -0.54 t ((s)) 1.2 1.4 1.6 1.8 2 x ((t)) ((in ))