APLICACIONES SOBRE LA ECUACIÓN DE BERNOULLI

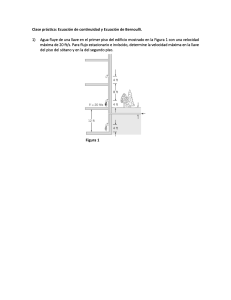
APLICACIONES
SOBRE LA
ECUACIÓN DE
BERNOULLI
PAZ HUMBO LUIS ALEXANDER
Docente:
Dr. José Carlos Albán Palacios
INTRODUCCIÓN
La ecuación de
Bernoulli es una
herramienta
fundamental en la
dinámica de fluidos
que describe el
comportamiento de
un fluido ideal en
movimiento. Esta
ecuación se puede
aplicar en una
variedad de
situaciones
prácticas y teóricas.
Aquí hay algunas
aplicaciones
comunes:
Diseño de Aeronaves:
La ecuación de Bernoulli se utiliza para
entender cómo el aire fluye sobre las alas
de un avión. La diferencia de presión entre
la parte superior e inferior del ala genera
sustentación, permitiendo que el avión se
mantenga en el aire.
Ingeniería de Tuberías y Sistemas de Agua:
En sistemas de tuberías, la ecuación ayuda
a calcular la presión y la velocidad del agua
en diferentes puntos de la tubería. Es
esencial para diseñar sistemas de
distribución de agua y para el análisis de la
pérdida de carga debido a fricción y otros
factores.
Medidores de Flujo:
Dispositivos como el tubo de Venturi
y el medidor de flujo de orificio usan
la ecuación de Bernoulli para medir
la velocidad del fluido. Estos
medidores se basan en el principio
de que la velocidad de un fluido
aumenta y la presión disminuye en
un estrechamiento de la tubería.
Sistemas de Ventilación:
La ecuación se aplica en
el diseño de sistemas de
ventilación y
calefacción, ayudando a
asegurar que el aire se
distribuya de manera
efectiva y que las
presiones en diferentes
partes del sistema sean
adecuadas para
mantener el flujo
deseado.
Hidrología y Gestión de Recursos Hídricos:
En la gestión de ríos y
presas, la ecuación de
Bernoulli se usa para
modelar y analizar el
flujo de agua, así como
para calcular el impacto
de diferentes
estructuras en el caudal
y la presión del agua.
Sistemas de Enfriamiento y Calefacción:
En sistemas de
enfriamiento y
calefacción, la ecuación
de Bernoulli se utiliza
para analizar el flujo de
aire a través de
intercambiadores de
calor y otros
componentes, ayudando
a mejorar la eficiencia
del sistema.
APLICACIONES SOBRE LA ECUACIÓN DE
BERNOULLI EN LA INGENIERÍA DE MINAS
1. Transporte de Minerales por Tuberías (Tuberías de Lodo):
En la ingeniería de minas, la
ecuación de Bernoulli tiene
varias aplicaciones cruciales,
particularmente en la gestión y
optimización de sistemas de
fluidos y transporte de
materiales. Aquí te detallo
algunas aplicaciones
específicas:
Diseño de Sistemas de
Transporte: En la minería, el
transporte de mineral en forma
de lodo a través de tuberías es
común. La ecuación de Bernoulli
ayuda a calcular la presión
necesaria para mover el lodo a
través de las tuberías,
considerando las pérdidas por
fricción y cambios en la velocidad
del fluido.
1
Un sistema de transporte de lodo en una mina utiliza una
tubería de 2000 metros de longitud y 0.4 metros de
diámetro para transportar una mezcla de mineral y agua
con una densidad de 1300 kg/m³. El caudal es de 0.1 m³/s y
la velocidad del lodo en el inicio de la tubería es de 1.5 m/s.
La pérdida de carga por fricción a lo largo de la tubería se
estima en un 10% de la presión dinámica.
Determina la presión en la entrada y salida:
Entrada: La presión en la entrada es de 150 kPa.
Salida: Usa la ecuación de Bernoulli para calcular la
presión en la salida.
2. PROBLEMA
En la figura fluye agua de la sección 1 en la
sección 2. La sección 1 tiene 25 mm de
diámetro, la presión manométrica es de
345 kpa y la velocidad de flujo es de 3 m/s.
La sección 2 tiene 50 mm de diámetro, está
a dos metros sobre la sección 1.
Suponiendo que no hay pérdidas, calcule la
presión P2. (g=10m/s²)
3. Estimación de Velocidades en Chancadores y Molinos:
Procesamiento de Minerales: Durante el
procesamiento de minerales en chancadores
y molinos, la ecuación de Bernoulli puede ser
utilizada para estimar las velocidades de los
fluidos (aire o agua) que afectan el
rendimiento de estos equipos.
3
El aire en un chancador se mueve con
una presión de entrada de 95 kPa y
una velocidad de 5 m/s. Si la presión
en la salida es de 70 kPa, calcula la
velocidad del aire en la salida. La
densidad del aire es de 1.2 kg/m³.
4. PROBLEMA
En un torrente de agua se sumerge un tubo doblado,
según se muestra en la figura. La velocidad de la
corriente con respecto al tubo es v=2.5m/s. La parte
superior del tubo se encuentra a h°=12cm sobre el
nivel del agua del torrente z tiene un pequeño
agujero. Hasta que altura h subirá el chorro de agua
que sale por el agujero.
5. PROBLEMA
El agua que se encuentra en un
depósito cerrado, está sometido a
una presión manométrica de 0,3
kg/cm² ejercido por aire
comprimido, introducido en la
parte superior del depósito. En la
pared lateral del mismo hay un
pequeño orificio situado 5 m por
debajo del nivel del agua. Hallar la
velocidad con la cual sale el agua
por este orificio. La sección
superior es mucho mayor que el
orificio.
6. PROBLEMA
En la concentración de la
tubería mostrada en la
figura, el agua fluye
constantemente con la
velocidad V1=0.5 m/s y
V2=1.125 m/s. Dos tubos
piezométricos están unidos
a la tubería en los puntos 1
y 2. Determine la altura H.
7. Modelado de Flujos en Celdas de Flotación:
Separación de Minerales: En las celdas de flotación,
donde se utilizan burbujas para separar minerales, la
ecuación de Bernoulli se aplica para entender y
optimizar el flujo de los fluidos, lo que puede afectar la
eficiencia del proceso de separación.
En una celda de flotación, el flujo de agua se mueve a
través de la celda y experimenta cambios en la presión.
Se sabe que:
La presión del agua en la entrada de la celda es de
150 kPa.
La velocidad del agua en la entrada es de 2 m/s.
La presión del agua en la salida de la celda es de 100
kPa.
La densidad del agua es 1000 kg/m3.
Pregunta:
Calcula la velocidad del agua en la salida de la celda.
8. PROBLEMA
Para el sifón de la figura mostrado en el
problema, calcule el flujo volumétrico de
aceite que sale del tanque.
9. PROBLEMA
Fluye agua continuamente de un tanque abierto como
se muestra en la figura. La altura del punto 1 es de 10
m, y la de los puntos dos y tres es de 2 m. El área
transversal en el punto 2 es de 6x10-⁴ m² ; en el punto 3
es de 3x10-⁴ m². El área del tanque es muy grande en
comparación con el área transversal del tubo.
Suponiendo que puede aplicar la ecuación de Bernoulli,
determine la rapidez de descarga en litros por
segundo. (g=10 m/s², √10 = 3.16)
10. PROBLEMA
Determine la
presión en el
tubo superior si
en la parte
inferior
presenta 89 kpa,
y fluye aceite a
razón de 0.9
m³/s.
GRACIAS