CINEMÁTICA y DINÁMICA 1º BACHILLER

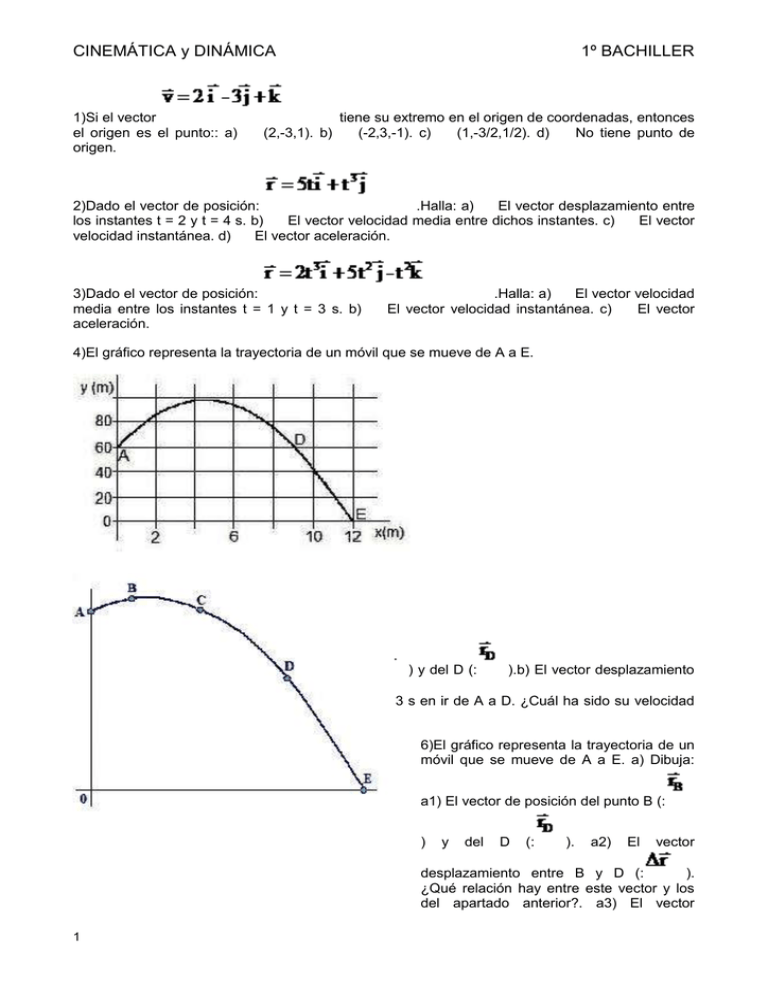
CINEMÁTICA y DINÁMICA
1)Si el vector
el origen es el punto:: a)
origen.
1º BACHILLER
tiene su extremo en el origen de coordenadas, entonces
(2,-3,1). b)
(-2,3,-1). c)
(1,-3/2,1/2). d)
No tiene punto de
2)Dado el vector de posición:
.Halla: a)
El vector desplazamiento entre
los instantes t = 2 y t = 4 s. b)
El vector velocidad media entre dichos instantes. c)
El vector
velocidad instantánea. d)
El vector aceleración.
3)Dado el vector de posición:
media entre los instantes t = 1 y t = 3 s. b)
aceleración.
.Halla: a)
El vector velocidad
El vector velocidad instantánea. c)
El vector
4)El gráfico representa la trayectoria de un móvil que se mueve de A a E.
5)Dibuja: a) El vector de posición del punto A (:
entre A y D (:
media?.
) y del D (:
).b) El vector desplazamiento
) c) Sabiendo que ha tardado 3 s en ir de A a D. ¿Cuál ha sido su velocidad
6)El gráfico representa la trayectoria de un
móvil que se mueve de A a E. a) Dibuja:
a1) El vector de posición del punto B (:
)
y
del
D
(:
).
a2)
El
vector
desplazamiento entre B y D (:
).
¿Qué relación hay entre este vector y los
del apartado anterior?. a3) El vector
1
CINEMÁTICA y DINÁMICA
1º BACHILLER
velocidad en el punto C (:
), así como
sus componentes. b) Sabiendo que el
movimiento total es la composición de dos
movimientos (uno en dirección x , de
ecuación: x = 3t y otro en dirección y de
ecuación: y = 6 + 6t - 4,9t2), halla la
ecuación de la trayectoria. c) Halla la
distancia 0-E.
7)El vector de posición de un móvil es
(m), siendo t el tiempo en segundos.
Calcula el vector velocidad instantánea en el momento en que su aceleración es 10 m/s2.
8)Un cuerpo se desplaza 5 m cada segundo hacia el norte y 2 m cada segundo hacia el este. Si
su posición inicial es (3,0), ¿cuál de las siguientes ecuaciones representa correctamente la
posición en función del tiempo?:a)
, b)
9)El vector de posición de una barca que cruza un lago es:
su trayectoria es:a) y = 2x + 6 b) y = 6x + c) y = 3x + 6
c)
. La ecuación de
10)En un movimiento rectilíneo uniformemente acelerado:a)La velocidad aumenta con el tiempo b)
La velocidad disminuye con el tiempo c) La aceleración aumenta con el tiempo.
11)En un movimiento rectilíneo uniformemente retardado:a)La velocidad es negativa, b)La
velocidad es positiva. c) La aceleración es negativa. d) La aceleración y la velocidad tienen
sentidos opuestos.
12)Un móvil inicia su movimiento en la posición x0 = 3 m, en el instante t0 = 0 y tiene un
movimiento
rectilíneo
cuya
gráfica
velocidad-tiempo
es
la
de
la
figura.
13)Determina: a)La ecuación de x en función de t, para el primer tramo y la posición en la que se
encuentra a los 5 s b) La aceleración y el desplazamiento para el tercer tramo
14)Un móvil, que se encontraba en la posición 0
cuando empezamos a contar el tiempo, tiene la
siguiente gráfica v-t.a) ¿Qué información se deduce de
dicha gráfica?. b) Representa la gráfica x-t.
15)Un automóvil pasa por la posición x = 25 m, con
una velocidad de – 10 m/s, en el instante en que
empezamos a contar el tiempo. Su aceleración es de
0,50 m/s2. a)
Escribe la ecuación del movimiento y
represéntala. b)
Escribe y representa la ecuación
2
CINEMÁTICA y DINÁMICA
1º BACHILLER
de su velocidad.c)
¿Cuál es su posición y velocidad
a los 20 s?. ¿Y a los 30 s?. d)
¿Cuál ha sido su
desplazamiento en el intervalo de 0 a 30 s?. ¿Qué
espacio ha recorrido?. e)
Describe el movimiento
que ha tenido el móvil.
16)En la figura se representan las gráficas
v-t de dos móviles que se mueven sobre la
misma recta.En el instante t = 0, el móvil A
se encuentra en la posición x0 = 20 m y el
B en la x0 = 80 m. ¿En qué instante y
posición chocan?.
Un niño corre a una velocidad constante de 2 m/s hacia un perro. Cuando está a 4 m de él, el
perro empieza a correr, alejándose en línea recta, con una aceleración de 0,2 m/s2. ¿En qué
instante y posición logrará alcanzar el niño al perro?. Explica las soluciones del problema.
Representa las gráficas x-t de ambos.
17)Un cuerpo se deja caer libremente desde una altura de 800 m. Simultáneamente se dispara un
segundo cuerpo, verticalmente desde el suelo, con una velocidad inicial de 200 m/s.
Calcular:a)
El tiempo que tardan en cruzarse. b)
La distancia a la que se cruzan.
18)Una grúa eleva un objeto pesado a velocidad constante de 10 m/s. Cuando el objeto se
encuentra a 5 m sobre el suelo, rompe el cable, quedando aquél en libertad. Se pregunta: a)
¿Hasta qué altura seguirá subiendo el objeto?. b)
¿Cuánto tiempo tardará en llegar al suelo
desde que se rompió la cuerda?.
19)¿Con qué velocidad se debe lanzar un objeto, inicialmente en reposo, de 2 kg de masa, si se
quiere que alcance una altura de 10 m?.
20)Dos objetos son lanzados verticalmente en sentidos opuestos, pero con velocidades iguales en
módulo. Razona la veracidad o falsedad de las siguientes propuestas, supuesto que no hay
rozamiento: a)
Llegan al suelo con la misma velocidad. b)
Tardan lo mismo en llegar al
suelo. c)
La velocidad con la que lleguen al suelo depende de la masa de cada uno.
21)En invierno, un estudiante de Física mira a la calle a través de un ventanal. En el instante t = 0
aparece una pelota por la parte inferior de la ventana, con velocidad desconocida. La pelota tarda
un tiempo t1= 0,5 s en desaparecer por la parte superior de la ventana y sigue subiendo, fuera ya
de la visual del estudiante, hasta el instante t2 = 0,7 s en que la pelota, que ahora cae, vuelve a
asomar por la parte superior de la ventana. Con estos datos, ¿qué valores calculará el estudiante
para la altura de la ventana y para la velocidad inicial de la pelota?.
22)Una bola cae desde 50 m de altura para incrustarse en la arena hasta una profundidad de 60
cm: a)¿Con qué velocidad entra en contacto con la arena?. b)¿Qué desaceleración, supuesta
constante, produce la arena?. c)¿Cuánto tiempo transcurre desde que entra en contacto con la
arena hasta que se frena?.
23)Partiendo del reposo, una esfera de 10 g cae libremente, sin rozamiento, bajo la acción de la
gravedad, hasta alcanzar una velocidad de 10 m/s. En ese instante comienza a actuar una fuerza
constante hacia arriba, que consigue detener la esfera en 5 segundos. a)
¿Cuánto vale esta
fuerza?. b)
¿Cuál fue el tiempo total transcurrido en estas dos etapas?.
24)Un ascensor sube con una velocidad constante de 2 m/s. Cuando se encuentra a 10 m sobre
el nivel del suelo los cables se rompen. Prescindiendo del rozamiento,a)
Calcula la máxima
altura a la que llega la cabina. b)
Si los frenos de seguridad actúan automáticamente, cuando
la velocidad del descenso alcanza el valor de 4 m/s, determina la altura en la que actúan los
frenos.Se deja caer libremente un cuerpo de 10 gramos y cuando su velocidad es de
3
CINEMÁTICA y DINÁMICA
fuerza.b)
recorrida.
1º BACHILLER
se le opone una fuerza que detiene su caída en 4 s. Calcula: a)
La distancia recorrida hasta el instante de aplicar la fuerza.c)
El valor de la
Distancia total
25)Desde un punto situado a una altura h, se lanza un objeto verticalmente hacia arriba con una
velocidad de 29,4 m/s. Desde el mismo punto se deja caer otro objeto, 4 s después de haber
lanzado el primero. ¿En qué instante y lugar alcanza el primer objeto al segundo?. ¿Qué
velocidad tiene cada uno de ellos en ese instante?.
26)Un cuerpo se deja caer libremente desde una torre y pasa por los puntos P1 y P2 en los
tiempos t1 y t2 respectivamente. Sabiendo que t2- t1 = 2 s y que su energía cinética en P2 es doble
que en P1, calcula: a)
El tiempo t1. b)
La distancia a la que están separados entre sí los
puntos P1 y P2 . Nota: Tomar g = 9,81 m/s
27)Un arquero lanza una flecha con una velocidad de 20 m/s y una inclinación de 30º respecto a
la horizontal. a) Halla la posición en la que se encontrará al cabo de 1,5 s y la velocidad que lleva
en ese momento. b) Halla la altura máxima. c) Calcula si alcanzará el centro de una diana que se
encuentra a 30 m de distancia y a una altura de 2,5 m sobre el punto de lanzamiento.
28)Desde un lugar situado a 30 m de altura, se lanza un proyectil con una velocidad inicial de 108
km/h y un ángulo de 40º respeto de la horizontal. a) Escribe las ecuaciones del movimiento. b)
Calcula el alcance y la altura máxima.c) Calcula la posición y velocidad a los 3 s del lanzamiento.
29)Un avión vuela a 500 m de altura con una velocidad horizontal de 720 km/h. En el instante en
que sobrevuela un punto P deja caer un objeto. Halla: a) La posición y velocidad del objeto a los 5
s. b) El punto de choque y la velocidad del objeto cuando llega al suelo.
30)Sobre una mesa de 0,65 m de altura, se mueve con velocidad constante de 4 m/s, una bola,
hasta que cae por uno de sus extremos. Halla: a) La ecuación de la trayectoria. b) La posición y la
velocidad a los 0,1 s. c) ¿Qué velocidad tendría a los 0,5 s?.
31)Un depósito elevado de agua tiene un orificio a 36 m de altura. Suponiendo que el agua sale a
una velocidad constante de 10 m/s, halla: a) El tiempo que tarda en llegar al suelo. b) La distancia
horizontal que alcanza. c) El ángulo y la velocidad de impacto con el suelo.
32)Desde una altura de 9 m, se lanza un objeto oblicuamente hacia abajo, con una velocidad
inicial de 20 m/s, en una dirección que forma un ángulo α con la horizontal, tal que sen α = - 0,6 y
cos α = 0,4. Halla: a) Las ecuaciones que nos permiten determinar su posición. b) El tiempo que
tarda en llegar al suelo y el punto en que lo hace. c) ¿Cuál ha sido el desplazamiento del
proyectil?. ¿Coincide con el espacio recorrido?. ¿Por qué?
33)Un esquiador especialista en la modalidad de salto, desciende por una rampa, que
supondremos un plano inclinado que forma 13º con la horizontal y de 50 m de longitud. El extremo
inferior de la rampa, se encuentra a 14 m sobre el suelo horizontal. Ignorando los rozamientos y
partiendo del reposo, calcula : a)
La velocidad que tendrá al abandonar la rampa de
lanzamiento. b)
La distancia horizontal que recorrerá en el aire antes de llegar al suelo.
34) Si un móvil da 10 vueltas cada 8 s, analiza las siguientes propuestas: a)
Su período es 1,25
s. b)
Su velocidad angular es 7,85 rad/s. c)
Su velocidad angular es 1,25 rpm.
35)Desde un mismo punto de una circunferencia, parten dos móviles en sentidos opuestos. El
primero recorre la circunferencia en 2,40 h y el segundo recorre un arco de 6º30’ por minuto.
Determina en que punto se encontrarán y el tiempo invertido.
36)¿En qué casos un movimiento circular tiene aceleración tangencial?. ¿Y normal?. ¿Y
angular?.¿Por qué?.
4
CINEMÁTICA y DINÁMICA
1º BACHILLER
37)¿Cómo afecta a la velocidad la existencia de aceleración tangencial?. ¿Y la existencia de
aceleración normal o centrípeta?.
38)Indica que tipo de movimiento describe un cuerpo si: a)
b)
Tiene
constante.
=0y
= constante. c)
Ambas son 0. d)
Tiene │
Tiene │
│= constante y
= 0.
│= constante y
=
39)¿Qué fuerza debe aplicarse a un cuerpo de masa 4 kg, que se mueve con una velocidad de 5
m/s, para que describa una circunferencia de 50 cm de radio sin que varíe el módulo de su
velocidad?. ¿Qué dirección deberá tener dicha fuerza?.
40)Un disco que giraba a 33 r.p.m., se para en 10 s. a) ¿Cuál es su aceleración de frenado? b)
¿Cuántas vueltas da hasta pararse? c) ¿Cuánto vale la aceleración tangencial y normal de un
punto situado a 10 cm del centro, a los 5 s de empezar a frenar?.
41)Un móvil puntual describe una circunferencia de 50 cm de radio. Partiendo con una velocidad
inicial de 0,2 m/s, se mueve con una aceleración angular constante de 0,6 rad/s2. Halla, al cabo de
9 s: a) El desplazamiento angular y el arco recorrido. ¿En qué posición se encuentra?. b) Su
aceleración tangencial, normal y total y dibújalas.
42)a) Dos ruedas, una de 1 cm de radio y otra de 0,25 cm de radio, giran solidariamente. La
primera da 20 vueltas en 4 s:
a)
Las dos tienen la misma velocidad lineal.
b)
La segunda también da 20 vueltas en 4 s.
c) La segunda da 5 vueltas en 4 s.
44)Una rueda dentada de 10 cm de radio hace girar a otra rueda dentada de 2 cm de radio. Si la
primera da 20 vueltas en 4 s, determina: a) Las velocidades angulares (en rad/s) de ambas
ruedas. b) El período y la frecuencia de la rueda pequeña.
45)Un cuerpo de 200 g de masa, gira en un plano vertical, a razón de 5 rad/s, atado al extremo de
una cuerda de 60 cm de longitud. Calcula: a) El valor de la tensión en el punto más alto de la
trayectoria. b) El valor de la tensión en el punto más bajo de la trayectoria. c) La distancia
recorrida por el cuerpo y el ángulo descrito por la cuerda en 0,2 s.
46)Calcular la profundidad de un pozo sabiendo que al dejar caer una piedra desde la boca del
mismo, escuchamos el impacto de la piedra con el fondo al cabo de 3 segundos. Dato: La
velocidad del sonido en el aire es de 340 m/s. Sol: 40´65 m
47)Expresa la velocidad lineal de un punto de la superficie terrestre situado a 30º de latitud norte.
(Considerar la Tierra como una esfera de radio R= 6.300 Km.) Sol: 396´65 m/s
48)El vector posición de un punto, en función del tiempo, viene dado por:
r(t)= t·i + (t2+2) j
(S.I.). Calcular: a) La posición, velocidad y aceleración en el instante t= 2 s.; b) El ángulo que
forman el vector velocidad y aceleración en el instante t= 2 s.; c) La aceleración media entre 0 y 2
segundos. Sol: r(2)= 2i + 6j m; V(2)= i + 4j m/s; a(2)= 2j m/s2; 14º; a= 2j m/s2
5
CINEMÁTICA y DINÁMICA
1º BACHILLER
49)El vector posición de un móvil viene dado por: r = 2·t2·i – 4·j (S.I.). Calcular: a) la velocidad
media entre 3 y 6 segundos; b) la velocidad instantánea; c) la aceleración a los 2 segundos y d) el
módulo de la aceleración tangencial. Sol: 18i m/s; 4ti m/s; 4i m/s2; 4 m/s2
50)Un pájaro parado en un cable a 5 metros sobre el suelo deja caer un excremento libremente.
Dos metros por delante de la vertical del pájaro, y en sentido hacia ella, va por la calle una
persona a 5 Km/h. La persona mide 1,70 m. Calcula; a) si le cae en la cabeza y b) a qué velocidad
debería ir para que le cayera encima.Sol: No le cae; 2´47 m/s
51)Un avión, que vuela horizontalmente a 1.000 m de altura con una velocidad constante de 100
m/s, deja caer una bomba para que dé sobre un vehículo que está en el suelo. Calcular a qué
distancia del vehículo, medida horizontalmente, debe soltar la bomba si éste: a) está parado y b)
se aleja del avión a 72 Km/h.Sol: 1414 m; 1131´2 m
52)Por la ventana de un edificio, a 15 metros de altura, se lanza horizontalmente una bola con una
velocidad de 10 m/s. Hay un edificio enfrente, a 12 metros, más alto que el anterior. A) ¿choca la
bola con el edificio de enfrente o cae directamente al suelo?. B) si tropieza contra el edificio ¿a
qué altura del suelo lo hace?. Tomar g= 10 m/s2.Sol: Da en el edificio de enfrente; 7´8 m
53)Calcular los módulos de la velocidad, aceleración tangencial y aceleración normal de un
cuerpo situado: a) en el ecuador y b) a 30º de latitud norte. (Suponer la Tierra esférica con un
radio de 6.300 Km)Sol: 458´15 m/s; 0 ; 0´033 m/s2; 396´6 m/s; 0; 0´0288 m/s2
54)Desde una azotea a 20 m de altura del suelo se lanza verticalmente hacia arriba una piedra
con velocidad de 25 m/s. Al mismo tiempo desde el suelo, se lanza otra piedra, también
verticalmente hacia arriba, con una velocidad de 30 m/s. Calcula: a) la distancia del suelo a la que
se cruzan y el tiempo que tardan en cruzarse; b) las velocidades de cada piedra en ese
instante.Sol: 41´6 m; 4 s; -14´2j m/s; -9´2j m/s
55)Una rueda de 15 cm de radio se pone en movimiento con una aceleración angular de 0,2
rad/s2. Halla el tiempo que tarda la rueda en dar 20 vueltas. Sol: 35´4 s
56)La velocidad de un móvil viene dada por las ecuaciones : Vx= 3 + 2·t2 y Vy= 3·t (S.I.). Calcular:
a) La velocidad al cabo de 1 segundo; b) La aceleración instantánea y su módulo.Sol: 5i + 3j m/s;
4ti +3j m/s2; (16t2 + 9)1/2 m/s2
57)Se dispara un proyectil formando un ángulo α con la horizontal y con una velocidad V.
Encontrar la ecuación del alcance máximo. (No dar a g valor numérico).Sol: x= V2sen 2α/g
58)Desde lo alto de una torre de 30 m de altura se deja caer una piedra 0,2 segundos después de
haber lanzado hacia arriba otra piedra desde la base a 15 m/s. Calcula el punto de encuentro
entre ambas piedras. Tomar g= 10 m/s2.
59)Un niño da un puntapié a un balón que está a 20 cm del suelo, con un ángulo de 60º sobre la
horizontal. A 3 metros, delante del niño, hay una alambrada de un recinto deportivo que tiene una
altura de 3 metros. ¿Qué velocidad mínima debe comunicar al balón para que sobrepase la
alambrada?.Sol: 8´64 m/s
60)La posición de un móvil viene dada por: x = 2t ; y = 2t2 – 1 , en el S.I.. Calcular: a) la ecuación
de la trayectoria; b) la velocidad instantánea; c) la aceleración a los 10 segundos.Sol: y= ½ x2 –1
m ; 2i + 4tj m/s; 4j m/s2
61)La velocidad de un móvil que sigue una trayectoria rectilínea viene dada por la ecuación: V(t) =
(t2-8t)j , en unidades del S.I.. Calcular: a) La aceleración media entre los instantes t = 2 s y t = 4 s.
; b) La aceleración instantánea en t = 3 s. y c) Las componentes intrínsecas de la aceleración en
cualquier instante.Sol: -2j m/s2; -2j m/s2; an=0 , atan= 2t – 8 m/s2
6
CINEMÁTICA y DINÁMICA
1º BACHILLER
62)Se lanza un proyectil desde lo alto de un acantilado de 150 metros de altura a 400 m/s con una
inclinación de 30º. Calcular : a) El tiempo que tarda en caer al suelo y b) La altura máxima que
alcanza.Sol: 40´73 s; 2150 m
63)Desde un punto situado a 100 m. sobre el suelo se dispara horizontalmente un proyectil a 400
m/s. Tomar g= 10 m/s2. Calcular: a) Cuánto tiempo tardará en caer; b) Cuál será su alcance; c)
Con qué velocidad llegará al suelo. Sol: 4´47 s; 1788´8 m; V= 400i – 44´7j m/s
64)Un coche se acelera desde el reposo con aceleración constante de 8 m/s2. ¿Con qué rapidez
marchará a los 10 segundos? ¿Cuánto habrá recorrido entonces? ¿Cuál es su velocidad media en
el intervalo de t = 0s a t = 10 s? Resp: a) 80 m/s b) 400 m
c) 10i m/s(i apunta en el sentido
de avance del móvil)
65)Un objeto con velocidad inicial de 5 m/s, que avanza siempre en el mismo sentido, tiene una
aceleración constante de 2 m/s2. Cuando su velocidad sea de 15 m/s, ¿qué distancia habrá
recorrido? (justifica bien el uso de tus ecuaciones)Resp: 50 m
66)Un vehículo pasa por un control de velocidad a 54 km/h. Entonces frena, de manera uniforme,
y se detiene a los 50 metros. Calcula la aceleración media del vehículo entre estos 2 instantes.
Calcula el tiempo de frenado. Calcula la aceleración instantánea del móvil en un instante
cualquiera de la fase de frenado. Escribe las ecuaciones vectoriales que dan posición y velocidad
del móvil en cada instante t Calcula la velocidad instantánea del móvil en los segundos 1s, 3s, 6s
y 9s desde que empezó a frenar. Suponiendo que los frenos transmiten al coche siempre la
misma aceleración, y que a 40 metros del punto donde comenzó a frenar se abre un precipicio ¿a
qué velocidad debería circular al pasar por el control, como máximo, para evitar una muerte
segura? Resp:
a) -2,25i m/s2 b) 6,67 s
c) -2,25i m/s2 e) v(1) = 12,75i m/s,
v(3) =
2
8,25i m/s
v(6) = 1,5i m/s v(9) = 0 d) r(t) = (15t - 1,125t )i m v(t) = (15 - 2,25t)i m/s f) v0 =
13,42i m/s
67)En t = 5s un perro está corriendo en línea recta para coger una pelota, a 5 m/s. En t = 8s su
velocidad es de 1 m/s en sentido contrario (vuelve con la pelota en la boca). Halla la aceleración
media del perro durante este intervalo. Suponiendo que el perro siga un movimiento de
aceleración constante (M.R.U.A.), ¿cuál es esta aceleración? ¿Con qué velocidad empezó a
correr el perro? ¿En que instante se paró el perro para coger la pelota? Si el perro empezó a
correr desde el punto en que su amo le lanzó la pelota, ¿a qué distancia se encontraba la pelota
cuando la recogió?. ¿Con qué velocidad llegará el perro triunfante al punto donde está el amo?
Resp: a) a5→8 = -2i m/s2
b) -2i m/s2
c) V(0) = 15i m/s d) A los 7,5s tras empezar a correr.
e) A 56,25 m. Llegará a -15i m/s
68)Un objeto sube por un plano inclinado, encontrándose a una velocidad de 10 m/s cuando está
a 6 metros del origen, y de 15 m/s cuando está a 10 m. ¿Cuál es su aceleración, supuesta
uniforme? ¿Qué tiempo tarda en recorrer esos 4m?. Resp:
15,63m/s2 en sentido de subida.
Tarda 0,32 s.
69)Un tranvía que parte del reposo, adquiere, al cabo de 20 m recorridos con movimiento
rectilíneo uniformemente acelerado, la velocidad de 36 km/h. Continúa con esta velocidad durante
1 min al cabo del cual, frena y disminuye uniformemente su velocidad hasta parar a 650 m del
punto de salida. Calcular la aceleración y el tiempo empleado en la primera fase del
movimiento.Calcular la aceleración y el tiempo empleado en la tercera fase del movimiento. Resp:
a) a = 2.5 ms-2, t = 4 s; b) a = 1.67 ms-2 y Δt = 6s.
70)Un automóvil está esperando que cambie la luz roja. Cuando la luz cambia a verde el auto
acelera uniformemente, durante 6 s, a razón de 2 m/s2; después de lo cual se mueve con
velocidad constante. En el instante en que el auto comienza a moverse, un camión que marcha
7
CINEMÁTICA y DINÁMICA
1º BACHILLER
en el mismo sentido, con movimiento uniforme de 10 m/s, lo pasa. ¿A qué tiempo y a qué
distancia se encontrarán nuevamente el auto y el camión?. Resp:
18 s; 180 m.
71)Se patea un balón de fútbol, verticalmente hacia arriba, con la rapidez inicial de 20 m/s. ¿Qué
altura alcanza el balón?¿Cuánto tarda en alcanzarla? ¿Cuánto tiempo está el balón en el
aire?¿Cuándo está la pelota a 15 m por encima del suelo? ¿Con qué velocidad llega de nuevo al
punto donde fue pateada? Resp:
a) 20,41 m
b) 2,05s y 4,1s.
c) A los 0,99s y
los 3,11s.
d) -20j m/s
72)Un rifle dispara una bala verticalmente hacia arriba, y esta vuelve al punto de partida al cabo
de 10s. Halla la velocidad inicial y la altura alcanzada.Resp:
49 m/s; 122,5 m.
73)Un estudiante, decidido a comprobar por sí mismo las leyes de la gravedad, se deja caer,
cronómetro en mano, desde un rascacielos de 280 m de altura. Cinco segundos más tarde
aparece en escena un superhombre y se lanza desde el tejado para salvar al estudiante.
74)¿Cuál debe ser la velocidad inicial del superhombre para que coja al estudiante justamente
antes de que éste llegue al suelo? ¿Cuál debería ser la altura del rascacielos para que ni aún el
superhombre pudiese salvar al estudiante?. Resp: a) 9.69 10 m/s; b) 1.23 102 m.
75)Una grúa eleva un objeto con la rapidez constante de 10 m/s. cuando el objeto se encuentra a
5m del suelo se rompe el cable, quedando aquel en libertad. ¿Hasta qué altura seguirá subiendo
el objeto? ¿Cuánto tiempo tardará en caer al suelo desde que se rompió la cuerda? Resp:
10.1 m; 2.45 s.
76)Una maceta cae desde una repisa de un edificio de apartamentos. Una persona de un
apartamento inferior, que dispone de un cronómetro observa que la maceta tarda 0.2 s en cubrir
la longitud de la ventana, que es de 4 m. ¿A qué altura sobre el borde superior de la ventana está
la repisa de la cual cayó la maceta Resp: A 18'46 m.
77)Desde un puente sobre un arroyo pirenaico un excursionista lanza una piedra verticalmente
hacia arriba a la velocidad inicial de 6m/s.¿Hasta qué altura se eleva la piedra?¿Cuánto tarda en
volver a pasar por el nivel del puente?. ¿Con qué velocidad lo hace?Si la piedra cae al río 1,94 s
después de haber sido lanzada,¿qué altura hay desde el puente a la superficie del agua?¿con
qué velocidad llega la piedra al agua?¿cuánto tardaría el excursionista en llegar al agua si se
dejara caer desde el puente?
Resp: a) 1,84 m b) 1,22s; a 6m/s c) 6,86 m d) 13,06 m/s e)
1,18s
78)Un cañón se ajusta con un ángulo de tiro de 600. Dispara una bala con una velocidad de 300
m/s¿A qué altura llegará la bala?¿Cuánto tiempo estará en el aire?¿Cuál es el alcance horizontal?
Resp: a) 34,44 m b) 0,53 s c) 79,53 m
79)Un motorista, equipado con su traje de buzo, salta con su moto desde el borde de un
acantilado de 183 m de altura, valiéndose de una rampa de inclinación 300 situada en el borde de
este.Si su rapidez era de 180 km/h. ¿cuánto avanza horizontalmente el motorista antes de
alcanzar el agua? Resp:
397,07 m
80)Se dispara un cañón con un ángulo de tiro de 150, saliendo la bala con rapidez de 200 m/s. Se
desea saber El alcance del proyectil. Velocidad con la que llega a tierra, en magnitud y dirección.
¿Tropezaría con una colina de 300 m de altitud que estuviera a la mitad de su alcance?En caso
afirmativo, ¿qué solución podríamos dar si quisiéramos dar en el mismo blanco sin cambiar de
cañón?Resp a) 2040,82 m b) 200 m/s a 150 bajo la horizontal c) Sí d) α=75o
81)Una avioneta vuela a 1500 m del suelo. En un cierto instante lanza un paquete de ayuda
humanitaria con un ángulo de 300 bajo la horizontal. Debido a la velocidad de vuelo del avión, la
rapidez del paquete en el momento de ser lanzado es de 100 km/h (respecto a tierra). ¿cuánto
tarda la ayuda en llegar al suelo y cuál será su recorrido horizontal? Resp: 16,14s y 388,30 m
8
CINEMÁTICA y DINÁMICA
1º BACHILLER
82)Una pelota de béisbol se lanza hacia un jugador con una velocidad inicial de 20 m/s, que forma
un ángulo de 450 con la horizontal. En el momento de lanzar la pelota, el jugador está a 50 m del
lanzador. ¿con qué velocidad y en qué sentido deberá correr el jugador para coger la pelota a la
misma altura que se lanzó? Resp: Debe correr a 3,18 m/s, hacia el lanzador.
83)El famoso cañón Berta (de la Primera Guerra Mundial) tenía un alcance máximo de 100 km.
Despreciando el rozamiento del aire, calcula:Velocidad del proyectil al salir por la boca del
cañón.Si ajustamos el cañón con un ángulo de 300 y el proyectil hace blanco en su descenso
sobre un objeto situado a 500 m de altura, ¿a qué distancia se encontraba dicho objeto?¿Cuál es
la velocidad de impacto? Resp: a) 989,95 m/s
b) 85,29 km
c) 984,92 m/s
84)Se dispara un proyectil , con α = 370. El disparo se hace desde un punto a 192m del borde de
un precipicio de 160m. El proyectil salva justamente dicho borde: Calcular la velocidad inicial del
proyectil. Hallar la distancia x que separa el punto de impacto del precipicio. Soluciones:
a)
44,24 m/s
b) 127,51 m
85)Un albañil trabaja sobre un tejado cuyos aleros miden 15m cada uno y forman un ángulo de 80º
entre sí. En un cierto instante deposita un martillo en el punto superior del tejado, pero este
desliza cayendo alero abajo. Sabiendo que el martillo resbala acelerando a razón de 6 m/s2.¿Con
qué rapidez sale despedido por el borde del tejado?¿cuánto tiempo tarda en llegar al borde?
86)Si el martillo cae a 7m de la casa,¿Cuánto tiempo tarda en caer en total?(desde la parte
superior del tejado)¿Cuál es la altura de la casa?Sugerencia: Resuelve los apartados a) y b) con
un sistema de coordenadas y cámbialo por otro para resolver c) y d).Resp:
a) 13,41 m/s b)
2,23 s c) 3,04 s d) 11,53 m
(1)Desde una terraza de 45m de altura se lanza un objeto en una dirección horizontal y perpendicular a la
pared del edificio de enfrente. Si la anchura de la calle es de 30m y el objeto impacta contra dicho edificio a
una altura de 15m del suelo:calcula la velocidad inicial aplicada a dicho objeto.¿cuál es el vector
velocidad del objeto en el momento del impacto?Resp: a) 12,12 m/s
b) 12,12i – 24,21j
m/s.Un automóvil marcha a 72 km/h. ¿ Qué aceleración negativa es preciso comunicarle para que
se detenga en 100 m ? ¿ Cuánto tiempo tardará en parar ? ¿ Cuál será la fuerza de frenado si la masa
del coche es de 1500 kg ?
( Sol.: -2 m/s2 ; 10 s ; -3000 N )
(2)Un autocar de 5 toneladas se mueve por una carretera horizontal sin rozamientos, y aumenta su
velocidad desde 54 km/h a 90 km/h en 2 minutos. ¿ Qué fuerza tuvo que hacer el motor ? ( S:
416,7 N )
(3)Un bloque de 5 kg está sostenido por una cuerda y es arrastrado hacia arriba con una aceleración
de 2 m/s2. Calcula la tensión de la cuerda. Si después de iniciado el movimiento la tensión de la
cuerda se reduce a 49 N, ¿que sucederá? ( Sol.: 59 N ; continuará con M.R.U. )
(4)Por la garganta de una polea pasa una cuerda de cuyos extremos cuelgan dos masas de 495 y 505
g. Si se desprecia el rozamiento de la cuerda y la masa de la polea, ¿ con qué velocidad se moverá la
masa mayor al cabo de 2 s ? ¿ Y la masa menor ? ( Sol.: 0,2 m/s y 0,2 m/s, son los módulos )
(5)Un avión comercial de 75 Tm necesita una pista de 2 km para conseguir la velocidad de
despegue. Si ésta es de 180 km/h, ¿ cuánto vale la fuerza de sus motores ? Despreciar los
rozamientos. (S: 46875 N )
(6)¿ Qué cantidad de movimiento posee un camión de 15 toneladas cuando se mueve con una
velocidad de 72 km/h ? ¿ Durante cuánto tiempo debe actuar una fuerza constante de 500 N para
detenerlo ? ¿ Qué espacio recorrerá hasta parar ? ( Sol.: 300.000 kg·m/s ; 600 s ; 6 km )
(7)Una piedra atada a una cuerda de 50 cm de longitud gira uniformemente en un plano vertical.
Hallar a qué número de revoluciones por minuto se romperá la cuerda sabiendo que su carga de
rotura es igual a 10 veces el peso de la piedra.
( Sol.: 126,89 rpm )
(8)Un hombre de 70 kg se encuentra en la cabina de un ascensor, cuya altura es de 3 m. Calcular: a/
La fuerza que soportará el suelo del mismo cuando ascienda con una aceleración de 2 m/s2.- b/ La
misma fuerza cuando descienda con la misma aceleración. c/ Si se desprende la lámpara del techo
en el primer caso, ¿ cuánto tiempo tarda en chocar con el suelo del ascensor ?
( Sol.: 826 N ;
545,8 N ; 0,7 s )
9
CINEMÁTICA y DINÁMICA
1º BACHILLER
(9)Una grúa eleva un peso de 2000 kp con un cable cuya resistencia a la ruptura es de 3000 kp. ¿
Cuál es la máxima aceleración con que puede subir el peso ?
( Sol.: 4,9 m/s2 )
(10)A una masa de 500 gramos se la hace girar en un plano horizontal mediante una cuerda de un
metro de longitud. Calcular : a/ La velocidad con que debe girar el cuerpo para que la cuerda forme
con la vertical un ángulo de 45º.- b/ El valor de la fuerza centrípeta en esas condiciones.- c/ La
tensión que ejerce la cuerda.
( Sol.: 2,63 m/s ; 4,9 N ; 7 N )
(11)Se deja caer libremente un cuerpo de 10 g de masa, y cuando su velocidad es de 20 m/s se le
opone una fuerza que detiene su caída en 4 s. a/ ¿ Cuánto debe valer dicha fuerza ? b/ ¿ Qué
espacio habrá recorrido hasta el momento de aplicar la fuerza ? c/ ¿ Qué espacio total habrá
recorrido hasta el momento de detenerse ?
(Sol.: 0,148 N ; 20,4 m ; 60,4 m )
(12)El motor de un automóvil ejerce una fuerza de tracción de 120 kp y el automóvil arrastra un
remolque con una cuerda. El automóvil tiene una masa de 800 kg y el remolque 1000 kg. Si se
desprecian los rozamientos, calcular: a/ La aceleración del movimiento.- b/ La tensión de la
cuerda. c/ La velocidad del conjunto cuando habiendo partido del reposo haya recorrido 20 m. (
Sol.: 0,65 m/s2; 652,7 N ; 5 m/s )
(13)Un dinamómetro está suspendido del techo de un ascensor. Del otro extremo pende un cuerpo
de 2 kg. Halla la fuerza que señala el dinamómetro cuando: a/ Sube con velocidad constante.- b/
Arranca con aceleración de un metro por segundo cuadrado. (Sol.: 19,6 N ; 21,6 N)
(14)De los extremos de una cuerda que pasa por la garganta de una polea fija de eje horizontal
penden dos masas de 4 kg cada una. Si inicialmente estaban a la misma altura, ¿qué masa habrá que
añadir a una de las dos, para que al cabo de 2 s las separe una distancia de 1,8 m? (Sol.: 0,385 kg)
(15)Una pelota de 120 g choca perpendicularmente contra un frontón cuando su velocidad es de 25
m/s, rebotando con la misma celeridad en un tiempo de 0,02 s. Calcula: a/ La variación del
momento lineal.- b/ La fuerza media de la pelota contra el frontón. (Sol.: 6 kg m/s ; 300 N)
(16)Calcula la velocidad de retroceso de un cañón de una t al disparar una granada de 10 kg con una
velocidad de 500 m/s. (Sol.: -5,05 m/s)
(17)Un cuerpo de 2 kg cae desde 20 m de altura sin velocidad inicial. ¿Cuánto ha variado su
momento lineal?
(Sol.: 39,60 kg m s-1)
(18)Un futbolista golpea el balón de manera que su pie está en contacto con el balón 0,15 s. El
balón, de masa 0,8 kg, sale disparado con una velocidad de 25 m/s formando 30 º con el suelo.
Calcula: a/ El momento lineal con el que sale el balón.- b/ la fuerza media que ejerce el jugador en
la patada. Sol.: 17,31i +10j kg m s-1 ; 133 N)
(19)Un cuerpo de 5 kg se desliza por una rampa inclinada 30º sobre la horizontal. La longitud de la
rampa es de 10 m y el coeficiente de rozamiento del cuerpo contra la rampa es de 0,2. Calcula: a/
La aceleración de caída del cuerpo por la rampa.- b/ La velocidad con que llega al suelo.
(
Sol.: 3,3 m/s2; 8,12 m/s)
(20)¿ Cuál es la velocidad a que puede ir un automóvil por una curva sin peralte, de radio 40 m, sin
derrapar, suponiendo que el coeficiente de rozamiento entre las ruedas y el suelo vale 0,5. ( Sol.: 14
m/s )
(21)¿ Durante cuánto tiempo debe actuar una fuerza horizontal de 90 N sobre un cuerpo de 20 kg
para que alcance una velocidad de 20 m/s sobre una superficie horizontal si el coeficiente de
rozamiento es 0,25 ? (Sol.: 9,75 s )
(22)Por un plano inclinado 30º sobre la horizontal se lanza hacia arriba un cuerpo de 5 kg, con una
velocidad de 10 m/s, siendo el coeficiente de rozamiento entre el cuerpo y el plano 0,2. a/ ¿Cuál
será la aceleración de su movimiento? b/ ¿Qué espacio recorre hasta que se para ? c/ ¿Qué tiempo
tarda en pararse ? Una vez que se para empieza a descender, ¿ con qué velocidad pasa por el punto
de partida? (Sol.: 6,5 m/s2; 7,6 m; 1,5 s ; 7 m/s )
(23)Una vieja máquina de vapor de 15 t arrastra una “composición” (así llaman a un tren los
ferroviarios) de dos vagones de 10 t cada uno. El tren arranca y el conjunto es arrastrado por una
fuerza de 50 kN. a/ Calcula la aceleración del tren.- b/ Calcula la fuerza que tienen que resistir los
enganches que unen los vagones. Piensa que la máquina tiene que tirar de dos vagones, pero el
primer vagón sólo tiene que tirar del segundo. (Sol.: 1,4 m/s2; 28 kN; 14 kN)
10
CINEMÁTICA y DINÁMICA
1º BACHILLER
(24)Un rifle de 4 kg dispara una bala de 20 g con una velocidad de 200 ms-1. ¿Cuál es la velocidad
de retroceso del arma? ¿Cuál es el momento lineal de la bala?
(Sol.: 1 m/s; 4 N s)
(25)Una ametralladora dispara balas de 20 g. Cada bala que sale del arma lleva un momento lineal
igual a 4,0 N s. a/ ¿Cuál es el momento lineal total de las 300 balas que dispara durante 60 s? ¿Qué
fuerza ha sido necesario aplicar al arma para proporcionar todo ese momento lineal?
(Sol.: 1,2
kN; 20 N)
(26)Cuando un futbolista golpea fuertemente un balón parado, lo “acompaña” impulsándolo durante
un tiempo, que en este caso es 8 ms. El balón, cuya masa es 0,43 kg, sale disparado con una
velocidad de 100 km/h.
(27)Calcula: a/ el momento lineal que imprime al balón; b/ la fuerza media F durante el contacto. (
Sol.: 12 N s; 1 kN)
(28)Un coche a 80 km/h choca de frente contra una pared, se deforma mucho y acaba parándose.
Todo lo que hay dentro del coche, incluido el conductor que va bien sujeto con el cinturón de
seguridad, recorre una distancia de 1,0 m antes de detenerse por completo. a/ Calcula la duración
del choque. b/ Calcula la aceleración del coche durante el frenado. (Sol.:90 ms; 25g)
(29)Dos bloques A y B, de 4 kg y 2 kg de masa respectivamente, se encuentran yuxtapuestos y
apoyados en una superficie horizontal. Se ejerce una fuerza horizontal sobre el bloque A, el cual
empuja a su vez al bloque B, que está en contacto con él. El conjunto experimenta una aceleración
de 2 m/s2 como consecuencia de la fuerza aplicada. ¿Cuál es la fuerza que soporta cada bloque?
(FA = 12 N; FB = 4 N)
(30)¿Qué fuerza han de ejercer los frenos de un coche de 1600 kg, que marcha con una velocidad de
108 km/h, para detenerse en un recorrido de 30 m? (Sol.: 24000 N)
(31)Un avión de 75 t necesita una pista de 2 km para conseguir la velocidad de despegue que, en
este caso, es de 180 km/h. ¿Qué fuerza han de ejercer los motores para conseguirla? ¿Qué tiempo
transcurre desde que inicia el recorrido hasta que despega? (Sol.: 46875 N; 80 s)
(32)Un cuerpo de 2 kg de masa se desliza por unb plano horizontal. Al pasar por un punto su
velocidad es de 10 m/s y se para 12 m más allá por el efecto del rozamiento. Calcula el coeficiente
de rozamiento. (Sol.: 0,425)
(33)Se lanza hacia arriba un bloque de 1 kg, a lo largo de la recta de máxima pendiente de un plano
inclinado 30º respecto del plano horizontal. El módulo de la velocidad inicial es 2 m/s y el
coeficiente de rozamiento es 0,3. Determine: a/ la distancia recorrida por el plano hasta que se
detiene y b/ la velocidad cuando se encuentra a la mitad de su recorrido. (Sol.: 0,268 m; 1,42 m/s)
(34)Dos bloques, ambos de masa 5 kg, están unidos por una cuerda de masa despreciable e
inextensible y deslizan hacia abajo por un plano inclinado que forma 60º con la horizontal. El
coeficiente de rozamiento con el plano del bloque que va delante es 0,6 y el del otro 0,7. la cuerda
se mantiene tensa durante el descenso y paralela a la línea de máxima pendiente. Determine: a/ la
aceleración de cada bloque, b/ la tensión de la cuerda y c/ el valor que debería tener el ángulo del
plano para que deslizasen por la pendiente con velocidad constante. Dato: g = 9,8 m s-2.
(Sol.:
5,3 m s-2 ; 1,24 N ; 33º )
(35)Un globo tripulado de masa total m = 900 kg desciende verticalmente con una aceleración a
=2,0 m/s2. Determine la carga (lastre) que es preciso arrojar para que el movimiento descendente se
convierta en vertical ascendente con el mismo módulo de velocidad. Considere que en la operación
el empuje se mantiene
(36)constante. Dato: g = 9,8 m s-2 . ( Sol.: 305 kg )
(37)Un cuerpo de 5 kg se desliza por una rampa inclinada 30º sobre la horizontal. La longitud de la
rampa es de 10 m y el coeficiente de rozamiento del cuerpo contra la rampa es de 0,2. Calcula: a/
La aceleración de caída del cuerpo por la rampa.- b/ La velocidad con que llega al suelo.
(
Sol.: 3,3 m/s2; 8,12 m/s)
(38)¿ Cuál es la velocidad a que puede ir un automóvil por una curva sin peralte, de radio 40 m, sin
derrapar, suponiendo que el coeficiente de rozamiento entre las ruedas y el suelo vale 0,5. ( Sol.: 14
m/s )
11
CINEMÁTICA y DINÁMICA
1º BACHILLER
(39)¿ Durante cuánto tiempo debe actuar una fuerza horizontal de 90 N sobre un cuerpo de 20 kg
para que alcance una velocidad de 20 m/s sobre una superficie horizontal si el coeficiente de
rozamiento es 0,25 ? (Sol.: 9,75 s )
(40)Por un plano inclinado 30º sobre la horizontal se lanza hacia arriba un cuerpo de 5 kg, con una
velocidad de 10 m/s, siendo el coeficiente de rozamiento entre el cuerpo y el plano 0,2. a/ ¿Cuál
será la aceleración de su movimiento? b/ ¿Qué espacio recorre hasta que se para ? c/ ¿Qué tiempo
tarda en pararse ? Una vez que se para empieza a descender, ¿ con qué velocidad pasa por el punto
de partida? (Sol.: 6,5 m/s2; 7,6 m; 1,5 s ; 7 m/s )
(41)Una vieja máquina de vapor de 15 t arrastra una “composición” (así llaman a un tren los
ferroviarios) de dos vagones de 10 t cada uno. El tren arranca y el conjunto es arrastrado por una
fuerza de 50 kN. a/ Calcula la aceleración del tren.- b/ Calcula la fuerza que tienen que resistir los
enganches que unen los vagones. Piensa que la máquina tiene que tirar de dos vagones, pero el
primer vagón sólo tiene que tirar del segundo. (Sol.: 1,4 m/s2; 28 kN; 14 kN)
(42)Un rifle de 4 kg dispara una bala de 20 g con una velocidad de 200 ms-1. ¿Cuál es la velocidad
de retroceso del arma? ¿Cuál es el momento lineal de la bala?
(Sol.: 1 m/s; 4 N s)
(43)Una ametralladora dispara balas de 20 g. Cada bala que sale del arma lleva un momento lineal
igual a 4,0 N /s. a/ ¿Cuál es el momento lineal total de las 300 balas que dispara durante 60 s?
¿Qué fuerza ha sido necesario aplicar al arma para proporcionar todo ese momento lineal?
(Sol.: 1,2 kN; 20 N)
(44)Cuando un futbolista golpea fuertemente un balón parado, lo “acompaña” impulsándolo durante
un tiempo, que en este caso es 8 ms. El balón, cuya masa es 0,43 kg, sale disparado con una
velocidad de 100 km/h. Calcula: a/ el momento lineal que imprime al balón; b/ la fuerza media F
durante el contacto. ( Sol.: 12 N s; 1 kN)
(45)Un coche a 80 km/h choca de frente contra una pared, se deforma mucho y acaba parándose.
Todo lo que hay dentro del coche, incluido el conductor que va bien sujeto con el cinturón de
seguridad, recorre una distancia de 1,0 m antes de detenerse por completo. a/ Calcula la duración
del choque. b/ Calcula la aceleración del coche durante el frenado. (Sol.:90 ms; 25g)
(46)Dos bloques A y B, de 4 kg y 2 kg de masa respectivamente, se encuentran yuxtapuestos y
apoyados en una superficie horizontal. Se ejerce una fuerza horizontal sobre el bloque A, el cual
empuja a su vez al bloque B, que está en contacto con él. El conjunto experimenta una aceleración
de 2 m/s2 como consecuencia de la fuerza aplicada. ¿Cuál es la fuerza que soporta cada bloque?
(FA = 12 N; FB = 4 N)
(47)¿Qué fuerza han de ejercer los frenos de un coche de 1600 kg, que marcha con una velocidad de
108 km/h, para detenerse en un recorrido de 30 m? (Sol.: 24000 N)
(48)Un avión de 75 t necesita una pista de 2 km para conseguir la velocidad de despegue que, en
este caso, es de 180 km/h. ¿Qué fuerza han de ejercer los motores para conseguirla? ¿Qué tiempo
transcurre desde que inicia el recorrido hasta que despega? (Sol.: 46875 N; 80 s)
(49)Un cuerpo de 2 kg de masa se desliza por unb plano horizontal. Al pasar por un punto su
velocidad es de 10 m/s y se para 12 m más allá por el efecto del rozamiento. Calcula el coeficiente
de rozamiento. (Sol.: 0,425)
(50)Se lanza hacia arriba un bloque de 1 kg, a lo largo de la recta de máxima pendiente de un plano
inclinado 30º respecto del plano horizontal. El módulo de la velocidad inicial es 2 m/s y el
coeficiente de rozamiento es 0,3. Determine: a/ la distancia recorrida por el plano hasta que se
detiene y b/ la velocidad cuando se encuentra a la mitad de su recorrido. (Sol.: 0,268 m; 1,42 m/s)
(51)Dos bloques, ambos de masa 5 kg, están unidos por una cuerda de masa despreciable e
inextensible y deslizan hacia abajo por un plano inclinado que forma 60º con la horizontal. El
coeficiente de rozamiento con el plano del bloque que va delante es 0,6 y el del otro 0,7. la cuerda
se mantiene tensa durante el descenso y paralela a la línea de máxima pendiente. Determine: a/ la
aceleración de cada bloque, b/ la tensión de la cuerda y c/ el valor que debería tener el ángulo del
plano para que deslizasen por la pendiente con velocidad constante. Dato: g = 9,8 m s-2.
(Sol.:
5,3 m s-2 ; 1,24 N ; 33º )
(52)Un globo tripulado de masa total m = 900 kg desciende verticalmente con una aceleración a
=2,0 m/s2. Determine la carga (lastre) que es preciso arrojar para que el movimiento descendente se
12
CINEMÁTICA y DINÁMICA
1º BACHILLER
convierta en vertical ascendente con el mismo módulo de velocidad. Considere que en la operación
el empuje se mantiene constante. Dato: g = 9,8 m s-2 . ( Sol.: 305 kg )
(53)Calcular la masa de un cuerpo que al recibir una fuerza de 20 N adquiere una aceleración de 5
m/s2. Sol: 4 kg.
(54)Calcular la masa de un cuerpo que aumenta su velocidad en 1,8 km/h en cada segundo cuando
se le aplica una fuerza de 600N. Sol: 1200 kg.
(55)Una fuerza tiene de módulo 4 N y forma un ángulo con el eje positivo x de 30º. Calcula las
componentes cartesianas. Sol: 3,5 i+2j
(56)El peso de un cuerpo en la Tierra es de 400 N. ¿Cuánto pesará ese cuerpo en la Tierra? Datos:
gluna = 1.63 m/s2. Sol: 2408 N.
(57)Dos cuerpos de igual masa caen desde 1 km de altura al suelo lunar y al suelo terrestre,
respectivamente. Si no se tiene en cuenta el rozamiento en la atmósfera terrestre, ¿en qué relación
se encuentran las velocidades al llegar al suelo? ¿Influye en la masa? Sol: v T = 2.45·vL. No
influyen las masas.
(58)El peso de un cuerpo en la Tierra, donde g = 9.81 m/s2, es 800 N. ¿Cuál es su masa y el peso en
la superficie de Júpiter? Dato: gJ = 25.1 m/s2. Sol: 81.5 kg, 2047 N.
(59)Halla la fuerza necesaria para detener en 8 s con deceleración constante: a) Un camión de 3000
kg que marcha a la velocidad de 80 km/h por una carretera recta y horizontal. b) Una pelota de 0.5
kg que va con una velocidad de las mismas características que el camión del apartado anterior. Sol:
a) –8333 N; b) –1.4 N.
(60)Un coche de 500 kg, que se mueve con velocidad constante de 120 km/h entra en una curva
circular de 80 m de radio. a) ¿Qué tipo de aceleración lleva? b) ¿Qué fuerza habrá que ejercer sobre
el coche para que no se salga de la curva? c) ¿Quién ejerce esta fuerza sobre el coche? Sol: a)
Centrípeta; b) 6931 N; c) El suelo mediante la fuerza de rozamiento.
(61)A un cuerpo de 20 kg le aplicamos una fuerza de 98 N. Halla la aceleración del cuerpo. ¿Qué
velocidad tendrá a los 5 s? Sol: 24.5 m/s2.
(62)¿Con qué fuerza hay que impulsar un cohete de 300 t, para que suba con aceleración de 11
m/s2? Sol: 6.24·106 N.
(63)¿Durante cuanto tiempo ha actuado una fuerza de 60 N inclinada 60º respecto a la horizontal,
sobre una masa de 40 kg situada en una superficie horizontal y sin rozamiento, para que alcance una
velocidad de10 m/s? Sol: 13.3 s.
(64)Un coche de 650 kg es capaz de adquirir una velocidad de 100 km/h en 8 s desde el reposo.
Calcula cuál será la fuerza total que actúa sobre él en la dirección del movimiento para conseguir
este resultado. Sol: 2256 N.
(65)Un elevador de 2000 kg de masa, sube con una aceleración de 1 m/s2. ¿Cuál es la tensión del
cable que lo soporta? Sol: 22000 N
(66)Una lámpara cuelga del techo de un ascensor que sube con una aceleración de 1.35 m/s2. Si la
tensión de la cuerda que sujeta la lámpara es de 72 N. a) ¿Cuál es la masa de la lámpara? b) ¿Cuál
será la tensión de la cuerda si el ascensor subiera frenando con la misma aceleración? Sol: a) 6.5 kg;
b) 54.9 N.
(67)Se arrastra un cuerpo de 25 kg por una mesa horizontal, sin rozamiento, con una fuerza de 70 N
que forma un ángulo de 60º con la mesa. a) ¿Con qué aceleración se mueve el cuerpo? b) ¿Qué
tiempo tardará en alcanzar una velocidad de 2 m/s, suponiendo que parte del reposo? Sol: a) 1.4
m/s2; b) 1.4 s.
(68) Un vehículo de 800 kg asciende por una pendiente que forma un ángulo de 15º con la
horizontal, recorriendo 32 m sobre el plano en 5 s. Suponiendo despreciable el rozamiento, calcular
la aceleración del vehículo y la fuerza que ejerce el motor. Sol: 2.56 m/s2 y 4077 N
(69)Se arrastra un cuerpo de 8 kg por una mesa horizontal, sin rozamiento, con una fuerza de 32 N
que forma un ángulo de 60º con la mesa. a) ¿Con qué aceleración se mueve el cuerpo? b)Si en el
instante de aplicar la fuerza se movía con una velocidad de 3 m/s, ¿qué velocidad habrá alcanzado a
los 5 s? Sol: a) 2 m/s2; b) 13 m/s.
13
CINEMÁTICA y DINÁMICA
1º BACHILLER
(70)Se arrastra un cuerpo de 45 kg por una mesa horizontal por la acción de una fuerza de 170 N
que forma un ángulo de 60º con la mesa. Si el coeficiente de rozamiento es 0.23, calcular: a) ¿Con
qué aceleración se mueve el cuerpo? b) ¿Qué tiempo tardará en alcanzar una velocidad de 6 m/s,
suponiendo que parte del reposo? Sol: a) 0.38 m/s2; b) 15.8 s.
(71)Calcula el coeficiente de rozamiento cinético para que un cuerpo descienda por un plano
inclinado 45 a velocidad constante. Sol: 1.
(72)Se arrastra un cuerpo de 36 kg por una mesa horizontal con una fuerza de 100 N paralela a la
mesa. Si el coeficiente de rozamiento es de 0.2, calcular: a) ¿Con qué aceleración se mueve el
cuerpo? b) ¿Qué tiempo tardará en alcanzar una velocidad de 1.3 m/s, suponiendo que parte del
reposo? Sol: a) 0.81 m/s2; b) 1.6 s.
(73)Un cuerpo de masa m = 10 kg esta apoyado sobre una superficie horizontal sin rozamiento. Una
persona tira del bloque con una soga fija al bloque, en dirección horizontal, con una fuerza de 20 N.
Calcular la aceleración del bloque, suponiendo despreciable la masa de la soga, y nulo el
rozamiento con el suelo. Sol: 2 m/s2.
(74)Dejamos caer una bola de 2 kg de masa y la Tierra la atrae con una fuerza (Peso de la bola) de
19.62 N. a) Con qué aceleración cae la bola. b) Si la masa de la Tierra es de 5.97·1024 kg. ¿Qué
aceleración adquiere la Tierra? Sol: a) 9.81 m/s2; b) 3.29·10–24 m/s2.
(75)Tenemos dos muelles de igual longitud, pero de constantes k 1 = 20 N/m y k2 = 20 N/m,
respectivamente. ¿Qué fuerza hay que realizar para alargar cada uno 10 cm? Sol: 2 N.
(76)Un muelle de constante k = 9 N/m se estira 3 m, ¿Calcular la fuerza a la que está
sometido el muelle? Sol: 27 N.
(77)El resorte de un dinamómetro de laboratorio se ha alargado 11.7 cm a tope de escala, que es 2
N. ¿Cuál es la constante del resorte con el que ha sido fabricado ese dinamómetro? ¿Cuánto se
alargará al aplicarle la fuerza de 0.4 N? Sol: 17.1 N/m, 2.3 cm.
(78)Un muelle de longitud 20 cm tiene una constante elástica de 6 N/m. a) ¿Qué intensidad tiene
una fuerza que produce un alargamiento igual a su longitud inicial? b) ¿A qué alargamiento da lugar
una fuerza de 0.28 N? c) ¿Qué longitud tendría el muelle del apartado anterior? Sol: a) 1.2 N; b) 4.7
cm; c) 24.7 cm.
(79)Un dinamómetro se alarga 4 cm a tope de escala, que es 1 N. ¿Cuál es su constante de
recuperación y cuanto marca si se alarga 2.5 cm? Sol: 25 N/m, 0.625 N.
(80) Un muelle horizontal de longitud l se comprime aplicando una fuerza de 50 N, hasta que su
longitud es de 15 cm. Si le aplicamos una fuerza de 100 N, su longitud queda
(81)reducida a 5 cm. a) ¿Cuál es la longitud inicial del muelle? b) ¿Cuánto vale su constante? Sol:
a) 0.25 cm; b) 500 N/m.
(82)Un resorte de 30 cm se alarga 5 cm al aplicarle una fuerza de 2.5 N. Calcula la constante y la
longitud del resorte cuando se le aplica otra fuerza de 4 N. Sol: 50 N/m, 38 cm.
(83)Que velocidad tendrá un tren, que partió del reposo, si sobre el actuó una fuerza de 104 N
durante 4 minutos. Su masa es 5·104 kg. Sol: 48 m/s.
(84) Una bala de 50 g y velocidad 200 m/s penetra 10 cm en una pared. Suponiendo una
(85)deceleración uniforme. Hallar: a) El tiempo que tarda en penetrar la pared b) La fuerza
constante que le opone la pared. Sol2·105 m·s–2, 1·10–3 s y 1·104 N.
(86)Un ciclista marcha a 15 km/h y choca de frente contra un vehículo aparcado. La
(87)duración del choque es de 0.3 s. Si el ciclista más la bicicleta tienen una masa de 92 kg
(88)¿Qué fuerza se ejerce durante el choque? ¿Hacia donde y con qué velocidad será desplazado el
ciclista? Sol: 1288 N, 15 km/h.
(89)Una fuerza de 20 N actúa sobre un cuerpo de masa 5 g durante 10 s, el cual inicia su
movimiento desde el reposo. ¿Qué espacio recorrerá el cuerpo en ese tiempo? Tomar gravedad 10
m/s2. Sol: 200 km.
(90)Sobre una bala de 10 kg, introducida en un cañón, actúa la pólvora con una fuerza de
(91)105 N. Hallar: a) La aceleración. b) El tiempo que tarda en recorrer los 2 m de longitud del
cañón y la velocidad de salida. Sol: a) 10000 m·s–2; b) 0.02 s y 200 m·s–1.
14
CINEMÁTICA y DINÁMICA
1º BACHILLER
(92)Una pelota de 300 g llega perpendicularmente a la pared de un frontón con una velocidad de 15
m/s y sale rebotada en la misma dirección a 10 m/s. Si la fuerza ejercida por la pared sobre la pelota
es de 150 N, calcula el tiempo de contacto entre la pelota y la pared. Sol: 0.05 s.
(93)Se quiere subir un cuerpo de 200 kg por un plano inclinado 30º con la horizontal. Si el
coeficiente de rozamiento cinético entre el cuerpo y el plano es 0,5 calcular: a) El valor de la fuerza
de rozamiento. b) La fuerza que debería aplicarse al cuerpo para que ascendiera por el plano a
(94)velocidad constante. Sol: a) 848.7 N; b) 1828.7 N
(95)Si un automóvil describe una curva de 50 m de radio, ¿cuál debe ser el mínimo valor del
coeficiente de rozamiento por deslizamiento entre las ruedas y el suelo para que el vehículo pueda
tomar la curva a 90 km/h? Sol: 1.27.
(96)Un camión de 13000 kg toma una curva de 200 m de radio a una velocidad de 50 km/h.
Suponiendo que no hay peralte, indicar la fuerza de rozamiento de las ruedas sobre el asfalto para
mantener el movimiento circular. ¿Qué valor tendrá la aceleración normal? Sol: 12539 N y 0.96
m/s2.
(97)Si un hombre de 60 kg se pesara en una pequeña báscula de baño, colocada sobre el suelo de un
ascensor que desciende con movimiento uniformemente acelerado de aceleración 0.4 m/s2, ¿qué
marcaría la báscula? Expresar el resultado en kp. ¿Cuál sería la respuesta si el ascensor descendiera
con una velocidad constante de 2m/s? Sol: 57.55 kp; 60 kp.
(98)Calcular la fuerza que ejerce sobre el suelo una persona de 90 kg que está en un
(99)ascensor, en los siguientes casos: a) sube con velocidad constante de 3 m·s–1. b) está parado.
c) baja con una aceleración constante de 1 m·s–2. d) baja con velocidad constante de 3 m·s–1. Sol:
a) 882 N; b) 882 N; c) 792 N; d) 882 N.
(100)Damos una patada a un balón parado con una fuerza media de 500 N. El balón, después de
recibir el golpe, sale lanzado con un ángulo de 45º con la horizontal y vuelve a tocar tierra a la
distancia de 40 m. Calcula el tiempo que dura el golpe dado al balón, cuya masa es de 0.42 kg.
Desprecia en todo momento el rozamiento del aire. Sol: 1.66·10–2 s.
(101)Arianne es el cohete espacial europeo. En el despegue, los dos motores propulsores laterales
producen una fuerza de 6713 kN cada uno. Si suponemos que la masa, 725 t, se mantiene constante
durante los 5 primeros segundos, calcula la velocidad que adquiere el cohete en ese tiempo,
expresada en km/h. Sol: 156.8 km/h.
(102)Dos masas unidas por un hilo inextensible y sin peso cuelgan de los extremos de una polea de
masa despreciable. En ausencia de rozamientos y despreciando los efectos debidos a la rotación de
la polea, calcula la aceleración si las dos masas son de 2 y 5 kg, respectivamente, así como la
tensión de la cuerda. Sol: 4.2 m/s–2; 28 N.
(103)Se ata una bola al extremo de una cuerda de 50 cm de longitud y se hace girar en el aire con
una velocidad de módulo constante. Si la cuerda forma un ángulo #= 30º con la vertical, calcula el
módulo de la velocidad de la bola y el tiempo que tarda en dar una vuelta completa. Sol: 20.8 m/s
(104)Una masa de 300 g gira en un círculo horizontal de 60 cm sobre una mesa sin rozamiento a
velocidad constante de una vuelta por segundo. La masa está unida mediante una cuerda que pasa
por un pequeño orificio de la mesa a otra masa m. ¿Cuál debe ser el valor de m para que el sistema
se mantenga en equilibrio? Sol: 0.72 kg.
15