La velocidad de soli.. - Tecnologia e Informatica en la ESO y
Anuncio

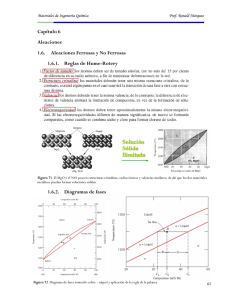
La velocidad de solidificación va a depender de la velocidad de nucleación y la de crecimiento de los núcleos . Estos procesos a al vez dependen de: La fuerza inductora del proceso , que es función de la velocidad de enfriamiento y el mecanismo de difusión, que depende de la temperatura provoca el movimiento de los agentes nucleantes por el material. La velocidad de nucleación se ve favorecida por un enfriamiento rápido. A temperaturas mas alejadas de la Te, creamos núcleos más rápidamente. Tenemos en el gráfico de la pagina 66 que el proceso de difusión crece a acercarnos a la Te y que la fuerza inductora es mayor al tener una Temperatura muy por debajo de la Te. La velocidad de nucleación se ve favorecida principalmente por la fuerza inductora y por tanto tenemos una velocidad pico en T2 ( lejos de Te ) La velocidad de crecimiento se ve favorecida por la Difusión, por tanto la velocidad pico esta muy cerca de Te Las propiedades mecánicas del material metálico son mejores al disminuir el grano medio del material. Para conseguirlo hay dos formas. 1º Aumentar la velocidad de nucleación, mediante un subenfriamiento o introduciendo agentes nucleantes. 2º Fragmentar los granos ya formados durante el crecimiento, mediante agitación intensa. Se define desde el punto de vista microestructural a una fase como parte homogénea de un material que difiere en composición, estado o estructura. En el caso del agua pura, tenemos tres fases,. Representamos su diagrama. En el caso de la congelación del agua ( procese del hielo ) tenemos dos fases a 0ºC, la líquida y la sólida. Tenemos tres líneas importantes en este diagrama. 1º Línea de Solidificación 2º Línea de Vaporación 3º Línea de Sublimación Y la unión de los tres crea este punto mágico donde coexisten las tres fases. Se le denomina punto triple. Pero si el punto es mágico, más lo es el propio diagrama. Veamos que ocurre con la línea de solidificación por encima de una atmósfera. Que se tuerce, que cambia la pendiente y esto que consecuencias tiene? Esto simplemente es un milagro. Pensemos en el fondo del mar. Si la pendiente no fuese negativa, a medida que bajamos al fondo, la presión aumenta además. Por otro lado, la temperatura es menor porque los rayos de sol ( su energía ) se queda en las capas mas superficiales ) . En este caso, baja temperatura y elevada presión tenemos que el agua cambiaría de estado ( hielo y fondos marinos congelados ) Pero gracias a esa pendiente negativa, según aumenta la presión, la temperatura para congelarse debe ser cada vez más pequeña, por tanto , el agua sigue en estado líquido permitiendo la existencia de vida en capas de agua inferiores. Regla de Fases de Gibbs Relaciona las variables que se pueden modificar en un diagrama de equilibrio. Se cumple que: f+g=c+2 Esto es: f = Número de fases existentes en el sistema g = Número de grados de libertad ( presión, temperatura y composición en sistemas de mas de un componente ) que se pueden modificar sin que varíe la fase del sistema. c = Número de componentes del sistema Ejemplos. Agua en el punto triple. Tenemos f = 3 y c = 1 ( el agua ), por tanto 3 + g = 1 + 3 -> El grado de libertad es cero. NO se puede tocar la presion o la temperatura sin que varíe el estado 2º Ejemplo. Un punto en estado líquido. En este caso, f = 1, c = 1 y g = 2. Se puede tocar la presión y la temperatura sin que varié el estado. Como en los procesos industriales, la presión es la atmosférica, se resta una variable y se utiliza la fórmula: f + g = c + 1. Diagramas de equilibrio en Aleaciones Al mantenerse la presión constante, podemos eliminar esta variable de la gráfica y hacerlo que solo dependa de la temperatura Un ejemplo lo tenemos en un diagrama de fases en una aleación de solubilidad total. Para interpretar este diagrama pensemos que en vertical nos movemos en temperatura y en horizontal en % de material, de esta forma, a la izquierda tenemos el 100 % de A y a la derecha el 100% de B. En el centro tenemos un 50% de cada uno. ¿ Cómo se produce la Solidificación ? A diferencia del metal puro donde se mantenía la temperatura en en proceso de cambio de estado, al existir dos componentes con distintos puntos de fusión, se va a originar un margen de temperaturas donde va a existir dicho proceso. Si nos fijamos en el diagrama , trazando una vertical , tenemos una temperatura inicial Ti y una Temperatura final Tf. La Ti es inferior a Ta, por tanto los cristales que se van a formar van a estar compuestos principalmente por átomos de A. Según bajamos, nos acercamos a la temperatura de fusion del material B, y los cristales que se va a formar van a contener, ahora, mayor proporción de átomos B. Entre las dos Temperaturas vamos a tener cristales mas líquido. Regla de la Horizontal que se encuentra una determinada aleación de composición química conocida. Así. - En el punto a, la aleación constituida por un 50% de a y 50% de B forma una solución sólida (alfa) de solubilidad total. - En un punto como el B la aleación se encuentra en un estado bifásico en el que coexisten un sólido y un líquido. - Y en el punto C la aleación se encuentra en estado líquido. La composición química de las dos fases se determina mediante la llamada regla de la horizontal: se traza una recta isoterma a la temperatura correspondiente al punto B y en sus puntos de corte con las líneas líquidus y sólidus se construyen rectas perpendiculares verticales; los puntos de intersección de estas últimas rectas con el eje de abcisas indican la composición de ambas fases. Regla de los segmentos inversos: Se utiliza la regla de los segmentos inversos para hallar el tanto por 1 en peso de la fase líquida. Para un punto situado en la bifase, tenemos: Cla y Clb como porcentajes de liquido de A y B Csa y Csb los porcentajes de solido en A y B y por último Wl tanto por 1 de la fase líquida y Ws el tanto por 1 de la fase sólida. Vamos a deducir como obtener el porcentaje de líquido de la solución. Se puede decir que: El porcentaje de liquido total x el porcentaje de liquido de A + El porcentaje de sólido x Porcentaje de sólido de A es el porcentaje total del elemento A Esto es: Wl * Cla + (1-Wl ) * Csa = Ca de donde wl = ( Csa - Ca ) / ( Csa - Cla ) Veamos el ejemplo de la pagina 71 Para la temperatura T2, tenemos que Csa = 85 y Cla = 35. Como el porcentaje total es 50 %, tenemos: wl = (85 - 50) / (85 - 35 ) = 0.7 y por tanto ws es 0,3. Si nos fijamos bien en el segmento, tenemos que dividimos el segmento desde el centro a el punto de solido (Csa - Ca ) entre el segmento total ( Csa - Cla ). Por esto se llama regla de los segmentos inversos. A mayor longitud el segmento que va a la línea de sólido, a mayor porcentaje de líquido. Aleaciones Eutécticas Qué es la temperatura de solidificación sino la temperatura a la que ya " no se encuentra cómoda el material en estado líquido " No tomemos esta definición como formal, pero si nos vale para entender un efecto curioso en aleaciones concretas. Se da la circunstancia de que para una determinada composición existe una estabilidad asombrosa en estado líquido y por tanto se "retarda" el proceso de solidificación. A la temperatura a la que ocurre esto, se la denomina temperatura Eutéctica. Veamos esto en un diagrama Si el componente es puro (a la izquierda del diagrama), la temperatura de fusión ( TA ) es aprox 1380ºC. Para B puro (a la derecha del diagrama) la fusión tiene lugar a 1485ºC. Si añadimos algo de B a A, por ejemplo, un 20% ( flecha roja) la temperatura de fusión (cristalización) se acerca a los 1360ºC. Hemos conseguido reducir la temperatura a la que empieza la solidificación Para una mezcla de 60% (flecha azul) en B, tenemos un proceso parecido. Cuando la concentración , para esta aleación, es del 50%, tenemos la temperatura mas baja, dando lugar al punto Eutéctico. ver procesos en http://www.uned.es/cristamine/mineral/quimica/quim_term_diag.htm domingo 26 Diagramas de equilibrio de aleaciones eutécticas con solubilidad parcial En el diagrama de la página 74 tenemos dos un punto eutectico E y dos sólidos diferentes α y β, cada uno de ellos con mayor proporción de los elementos A y B, de forma que α tendrá mas elemento A y β mas del B. El gráfico anterior corresponde a dos elementos que no son nada soluble, y esto no es lo normal. En el tipo I, se produce la solidificación a T constante con formación de compuesto α y β. Estos compuestos van cambiado su composición según se enfrían ( aplicar regla de segmentos inversos ) Para el tipo III. En este caso, en T2 se produce solidificación , formándose sólido de tipo α, terminado en T3, sin producirse el elemento β. Ejemplo: Sobre el diagrama de fases Cu-Ag, averiguar: a) Rango de aleaciones que sufrirán la transformación eutéctica. b) Si la aleación tiene un 30% de Ag, calcular que composición y que proporción de fases se tiene para las temperaturas de 500 y 900°C . c) Representar gráficamente la estructura a 500°C. Solución: a) Las transformación eutéctica ocurre cuando la mezcla atraviesa la isoterma eutéctica de 780°C., por tanto son todas las aleaciones que van desde el 7.9% hasta 91.2% de Ag. b) Empecemos a la temperatura de 900°C: La aleación en estado bifásico con L + compuesto . Para calcular la composición, trazamos la isoterma. El punto de corte col las líneas de solidus y liquidus nos dan los valores Fases Composición Proporción 7% Ag (41-30)/(41-7)= 32.35 % L 41% Ag (30-7)/(41-7)= 67.65 % A 500ºC, la aleación ya es sólida, con compuestos + . Trazamos la horizontal hasta llegar a la líneas de por la izquierda y por la derecha. A partir de los valores de composición pueden calcularse las proporciones de cada fase, aplicando la regla de la palanca: Fases Composición Proporción 3% Ag (98-30)/(98-3) = 71.58 % 98% Ag (30-3)/(98-3) = 28.42 % Si seguimos aplicando la regla de la palanca a una temperatura inferior, tendríamos que la composición del material cambaría. Tendríamos mas en detrimento de la c) Qué tenemos a 500°C ?. Anteriormente hemos calculado la cantidad exacta de cada fase y composición. Ahora debemos averiguar cómo se distribuyen éstas fases. La aleación sufre una transformación eutéctica y por tanto, e la estructura estará formada por: granos de , que solidifican en el seno del líquido al enfriarse entre los 940 y los 780°C. granos de mezcla eutéctica, cuando solidifica la ultima parte de líquido, de composición eutéctica. Un calculo muy aproximado se puede obtener aplicando la regla de la palanca entre la línea de la izquierda y el punto de composición eutéctica: 71.9% Ag. Constituyentes: E Proporción: Vista de los granos (71.9-30)/(71.9-3) = 60.81 % (30-3)/(71.9-3) = 39.19 % Domingo 26 2º parte Los procesos de solidificación que hemos visto son en condiciones mas ideales que reales. El proceso industrial, aún controlado, nos lleva a una curva que difiere de las reales. En la pagina 75 tenemos como se desplaza la línea de solidus a la izquierda como consecuencia de la velocidad de enfriamiento. En ese caso, lo mas destacable es cómo se superponen granos de alfa, con características algo diferentes. En el caso del α2, el grano se forma sobre granos α2, que sirven de elemento nucleante. Al final se forman los granos propios de la aleación. La junta de granos se ha formado por componentes de menor punto de fusión y esto puede ser un grave problema para las características del material. La forma de solucionarlo es por recocido, donde aumentamos la temperatura del compuesto ( por debajo deTf ) para que por difusión se reestablezca el equilibrio. Transformaciones en estado sólido Desde que se forma el sólido hasta que es utilizado a temperatura ambiente ( o en su entorno ), ocurren diversos procesos dentro del material ocasionados por la difusión atómica. La velocidad de este proceso es función de los defectos esetructurales. Las curvas TTT ( tiempo-temperatura-transformación ) son las empleadas para el estudio de los cambios que ocurren el el material En la gráfica superior se explica un poco que ocurre en un diagrama Fe-Carbono. Partiendo de la Austenita estable, bajamos a una temperatura de casi 700 ºC y la mantenemos, pasaremos de una austenita inestable a Perlita. De esta primera gráfica, es importante observar la línea verde que nos indica la velocidad de enfriamiento. Según sea, tendremos como resultado Perlita o Bainita. Veamos un segundo gráfico realizado por los amigos portugueses. En este caso, vemos claramente que tipo de granos tenemos según el proceso de enfriamiento en la gráfica TTT. Si se enfria muy rápido para llegar a la zona de la Martensita, tendremos la ausencia de tanto Perlita como Bainita. En estos gráficos se puede decir que tenemos fases metaestables ( izquierda ) y las estables, obtenidas a la derecha.