Aplicaciones de la primera y segunda derivada en las graficas de funciones

Lcdo. Eliezer Montoya
Matemática I
1
Universidad Nacional Experimental Politécnica de las Fuerzas Armadas
Núcleo Barinas
Asignatura Matemática I código 21214 –Primera Versión 14-06-08
Facilitador: Licdo Eliezer Montoya Sección(es) C y H
Aplicaciones de la Derivada: Representación Gráfica de Funciones)
usando el criterio de la primera y segunda derivada Representación
Gráfica de Funciones)
Para la representación gráfica de funciones utilizando la derivada se siguen los
siguientes pasos:
1) Determinar el dominio y el rango de la función
2) Calcular los puntos de corte:
a) Con el eje x (se hace y = 0)
b) Con el eje y (se hace x = 0)
3) Determinar puntos críticos (Xc ) y puntos de discontinuidad (si
existen)
Punto Crítico: Un valor c perteneciente al dominio de una función se
llama punto critico si f´(c) = 0 ó f´(c) no existe
4) Determinar los intervalos de crecimiento y decrecimiento:
a) Los puntos críticos y los valores donde el dominio de la función es
discontinua dividen el dominio en intervalos.
b) Se examina el signo de f´(x) en cada uno de esos intervalos , tomando
cualquier valor de x perteneciente a dicho intervalo (supongamos x=a) y
sustituyendo luego en f´(x)
c) Si f´(a) > 0 (la función crece en el intervalo.
Si f´(a) < 0 la función decrece en el intervalo
Lcdo. Eliezer Montoya
Matemática I
2
5) Hallar punto(s) máximo(s) y mínimo(s) relativo(s):
Se puede maximizar o minimizar
global y localmente una función
representativa de algún contenido
específico. Por ejemplo, en la
siguiente gráfica se representan
Máximos y Mínimos locales de la
función
: donde
Mínimos de
;
Máximos de
.
y
y
son
son
Según el criterio de la primera derivada:
a) Cuando la función pasa de ser creciente a ser decreciente, es decir,
cuando f´(x) > 0 pasa f´(x) < 0, entonces en el punto critico (a) se
considera que hay un máximo relativo. (esto es P(a, f´(a)) es un máximo
relativo)
b) Cuando la función pasa de ser decreciente a ser decreciente, es decir,
cuando f´(x) <0 pasa f´(x)> 0, entonces en el punto critico (b) se
considera que hay un mínimo relativo (esto es P(b, f´(b)) es un mínimo
relativo )
Lcdo. Eliezer Montoya
Matemática I
3
Según el criterio de la segunda derivada
*Se calcula f ´´(x )
y se halla la imagen de cada punto critico a través
de f ´´(x) .
*Si f ´´(a ) > 0 entonces f(a) es un mínimo relativo
* Si f ´´(a ) < 0 entonces f(a) es un máximo relativo (suponiendo que a es
un punto critico).
6) Determinar puntos de inflexión: Son los valores de x en donde la
segunda derivada es igual a cero ( f ´´(x) = 0) ó f ´´(x) no existe y hay un
cambio en la concavidad.
7) Estudiar la concavidad de la función:
Una vez determinados los puntos de inflexión ( si los hay), se debe tener
presente que estos dividen el dominio de la función en intervalos; se
‘procede a estudiar el signo de f ´´(x) en cada intervalo:
*Si f ´´(x) > 0 entonces f(x) es cóncava hacia arriba.
*Si f ´´(x) < 0
entonces f(x) es cóncava hacia abajo.
En conclusión, para cumplir con los pasos anteriores (del 5º al 7º ) se tiene
que Para estudiar el comportamiento de la curva que representa a la función
en ciertos intervalos, y en definitiva encontrar máximos y mínimos, debemos
realizar el siguiente procedimiento:
es una Función Real y Continua:
Considerando que
a) Determinar
b) Hacer
y obtener los valores críticos
c) Determinar
d) Evaluar
obtenidos
.
.
con los valores críticos
y examinar los signos
Si
entonces existe un Punto Mínimo (Min)
Si
entonces existe un Punto Máximo (Máx.)
Si
entonces existe un Punto de Inflexión (Inf)
Un punto se llama de inflexión si en él, la función, cambia el
sentido de la concavidad.
Lcdo. Eliezer Montoya
Matemática I
4
e) Evaluar la función original con los valores críticos y determinar los
.
puntos críticos, es decir
8) Determinar Asíntotas (si existen)
Asíntotas verticales : Dada la función f y la recta vertical x = a ;se dice que
x=a es una asíntota vertical de f sii:
y
lim f ( x) = ±∞
x→a +
lim f ( x) = ±∞
x →a −
Asíntotas horizontales: Dada la función f y la recta y = b ; se dice que y=b es
una asíntota horizontal de f sii :
lim f ( x) = b
x → +∞
y
lim f ( x) = b
x → −∞
Asíntotas oblicuas: Dada la función y= mx+b , se dice que y =mx+b es una
asíntota oblicua de f sii:
m = lim
x → ±∞
f ( x)
x
b = lim [ f ( x ) − m( x) ]
x → ±∞
9) Con toda la información obtenida en los pasos anteriores, se procede a
construir la grafica
Veamos un ejemplo:
1) Graficar
la función
.
Solución
1)Dominio y Rango de la función:
Dom f(x) = R = (−∞,+∞)
Rgo f(x) = R = (−∞,+∞)
2) Cortes con los ejes
Corte con el eje y : se hace x =0 y se obtiene que y = 8 es decir el punto (0,8)
Corte con el eje x: se hace y =0 y se obtiene 0= x3-6x2+9x-8 tiene una raíz
( 349/80,0) =( 4,3625;0)
3) Intervalos de crecimiento y decrecimiento
Determinamos la primera derivada de f y la igualamos a cero
Lcdo. Eliezer Montoya
Matemática I
5
De donde obtenemos que
La función es creciente en el intervalo (− ∞,1] U [3,+∞ ) , es decir, f´(a) > 0
donde a es un punto dentro del intervalo.
La función es decreciente en el intervalo comprendido entre [1,3], es decir,
f´(a)<0
5)Hallar punto(s) maximo(s) y mínimo(s) realtivo(s)
Ahora obtenemos la segunda Derivada y evaluamos en ella los valores críticos
Como
, entonces decimos que la función tiene un mínimo en
De la misma forma, considerando que
máximo en
serían:
.
, se dice que la función tiene un
. En definitiva, los puntos mínimos y máximo de la curva,
que es el punto mínimo de
•
la función, y
que es máximo de la
•
función.
6) Determinamos puntos de inflexión:
Además, si hacemos
, se tiene que:
es un punto de inflexión, en consecuencia:
es el punto de inflexión.
Lcdo. Eliezer Montoya
Matemática I
Finalmente se tiene que:
(1,-4) es un punto máximo de f
(3,-8) es un punto mínimo de f
(2,-6) es un punto de inflexión
7) Estudiamos la concavidad:
(−∞,2) Es cóncava hacia abajo, el signo de f´´(a) >0
(2,+∞) Es cóncava hacia arriba, el signo de f´´(a) <0
La grafica de f ( x) = x 3 − 6 x 2 + 9 x − 8 es:
Ejercicios propuestos:
(I) Graficar las siguientes curvas haciendo uso de de las derivadas:
6
Lcdo. Eliezer Montoya
Matemática I
7
8) f ( x) = 4 − x 2
x
9) f ( x) =
x+3
x−2
10) f ( x) =
x − .5
x+2
11) f ( x) =
x − .2
x( x + 1)
12) f ( x) =
( x + 3) 2
1) f ( x) = x 2 − 2 x − 3
2) f ( x ) = − x 2 + 4 x
3) f ( x) = x 3 − 2 x 2 − 5 x + 6
4) f ( x) = x 3 − x 2 + 4 x − 4
5) f ( x) = x 4 − 6 x 2 + 2
6) f ( x) = ( x 2 + 5 x + 4)( x 2 − 4 x + 3)
13) f ( x ) = − x.e1 / x
7) f ( x) = x 4 − 4 x + 2
14) f ( x ) = sin 2 x,
0 ≤ x ≤ 2π
Nota *Verifique dichas graficas en un software matemático, Use
modellus la aplicación de física o graphmatics u otro que este a su alcance
(II ) Calcular los puntos máximos y mínimos de las funciones siguientes
a) h( x) =
4x
1+ x2
c) f ( x) = x 1 / 3 .( x − 1) 2 / 3
e) f ( x) =
x
en el intervalo
x +1
b) g ( x) =
x3 −1
x
3

d) f ( x) = x 3 − 3 x + 3 en el intervalo − 3, 
2

 1 
− 2 ,1


Lcdo. Eliezer Montoya
Matemática I
8
Referencias bibliográficas:
:
*Stewart,
J. (1999) Cálculo conceptos y contextos. Editorial Thomson.
*Purcel, E. y Varberg, D. (2001). Cálculo con Geometría Analítica. Octava
Edición. Editorial Prentice Hall Hispanoaméricana. México
*Leithold, L. (1998) El Calculo VII edición. Edit Oxford
*Munem M.A. Foulis D.J. (1984) Calculus with Analytic Geometry . II
edicion.Edit. Worth Publishers, Inc. USA.
Lcdo. Eliezer Montoya
Matemática I
9
Soluciones de los ejercicios propuestos
Graficar las funciones siguientes usando el criterio de la primera y segunda la derivada
(para la representación grafica se uso el software Graphmatics y funciones para Windows)
1) f(x) = x2 -2x-3
f(x) = x2 -2x-3
Nombre de la función
1-Dominio f(x)
Rango f(x)
2.-Corte con los ejes
Función Cuadrática:
y =x^2-2x-3
Rgo f(x) = R
Dom f(x) = R
3.-Puntos críticos donde
f´(x) =0
4.-Intervalos de crecimiento
y decrecimiento
* f´(a)>0 → crece ,
* f´(a)<0 → decrece
5.-Coordenadas del punto
Máximo y Mínimo
f´(xc) >0 → Mínimo
f´(xc)<0 → Máximo
6.-Puntos de inflexión
f´´(x) = 0
f´´(x)>0 → cóncava hacia
arriba
f´´(x)<0 → cóncava hacia
abajo
7.-Asintotas.
Corte con el eje X
(-1,0) y (3,0)
F´(x)=2x-2
0 = 2x-2
entonces
− ∞,1 decrece
Corte con el eje Y
(0,-3)
Xc= 1
(
]
(− ∞,−1] ∪ [− 1,1] decrece
[1,+∞) crece
[1,3] ∪ [3,+∞ ) crece
Máximo : (xc, f(xc))
Max: No hay
Mínimo: ( xc , f(xc))
Min : (1,-4)
f´´(x)=2
Cóncava hacia arriba pues la
segunda derivada es positiva
No presenta asintotas
Con la información anterior se procede a graficar la función:
6 y
4
2
x
0
-6
-4
-2
0
-2
-4
-6
2
4
6
Lcdo. Eliezer Montoya
Matemática I
10
2) f(x) = - x2 + 4x
f(x) = -x2 +4x
Nombre de la función
1-Dominio f(x)
Rango f(x)
2.-Corte con los ejes
Cuadrática:
y =-x^2+4x
Rgo f(x) = R
Dom f(x) = R
3.-Puntos críticos donde
f´(x) =0
4.-Intervalos de crecimiento
y decrecimiento
* f´(a)>0 → crece ,
* f´(a)<0 → decrece
5.-Coordenadas del punto
Máximo y Mínimo
f´(xc) >0 → Minimo
f´(xc)<0 → Maximo
6.-Puntos de inflexión
f´´(x) = 0
f´´(x)>0 → cóncava hacia
arriba
f´´(x)<0 → cóncava hacia
abajo
8.-Asintotas.
Corte con el eje X
(0,0) y (4,0)
F´(x)=-2x+4
0 = -2x+4
entonces
− ∞,0 crece
Corte con el eje Y
(0,0)
Xc= 2
(
]
(− ∞,0] ∪ [0,2] crece
[2,+∞) decrece
[2,4] ∪ [4,+∞ ) decrece
Máximo : (xc, f(xc))
Max: (2,4)
Mínimo: ( xc , f(xc))
Min : No hay
f´´(x)=-2
Cóncava hacia abajo pues la
segunda derivada es positiva
No presenta asintotas
Con la información anterior se procede a graficar la función
6 y
4
2
x
0
-6
-4
-2
0
-2
-4
-6
2
4
6
Lcdo. Eliezer Montoya
Matemática I
11
3) f(x) = x3- 2x2 - 5x+6
Nombre de la función
f(x) = x3- 2x2 - 5x+6
Cúbica:
y=x^3-2x^2-5x+6
1-Dominio f(x)
Rango f(x)
2.-Corte con los ejes
3.-Puntos críticos donde
f´(x) =0
4.-Intervalos de crecimiento
y decrecimiento
* f´(a)>0 → crece ,
* f´(a)<0 → decrece
5.-Coordenadas del punto
Máximo y Mínimo
f´(xc) >0 → Minimo
f´(xc)<0 → Maximo
6.-Puntos de inflexión
f´´(x) = 0
7.- Concavidad:
f´´(x)>0 → cóncava hacia
arriba
f´´(x)<0 → cóncava hacia
abajo
8.-Asintotas.
Dom f(x) = R
Rgo f(x) = R
Pto de Corte con el eje X
(-2,0) , (1,0) y (3,0)
2
F´(x) = 3x -4x-5
2
0 = 3x -4x-5 entonces las
0.78
− ∞,−0.78 crece
Pto de Corte con el eje Y
(0,6)
(
]
(− ∞,−1] ∪ [− 1,−078] crece
raices son x1c= 2,11 y x2c = -
[− 0.78,+2.11) decrece
[− 0.78;1] ∪ [1;2.11] decrece
[2.11;+∞) crece
[2.11;3] ∪ [3;+∞ ) crece
Máximo : (xc, f(xc))
Max: (-0.78; 8.21)
Mínimo: ( xc , f(xc))
Min : (2.11;-4.06)
f´´(x)=6x-4
0 = 6x-4 → x=2/3=0.66..
Coordenada del pto. de
inflexión
(0.6 ; 2.2 )
(− ∞,2 / 3] cóncava hacia
[2 / 3,+∞ )
abajo
Cóncava hacia arriba
No presenta asintotas
Con la información anterior se procede a graficar la función
Lcdo. Eliezer Montoya
Matemática I
12
4) f(x) = x3- x2 +4x-4
Nombre de la función
3
f(x) = x
- x2 +4x-4
Cúbica:
y=x^3-x^2+4x-4
1-Dominio f(x)
Rango f(x)
2.-Corte con los ejes
3.-Puntos críticos donde
f´(x) =0
4.-Intervalos de crecimiento y
decrecimiento
* f´(a)>0 → crece ,
* f´(a)<0 → decrece
5.-Coordenadas del punto
Máximo y Mínimo
f´(xc) >0 → Minimo
f´(xc)<0 → Maximo
6.-Puntos de inflexión
f´´(x) = 0
7.- Concavidad:
f´´(x)>0 → cóncava hacia
arriba
f´´(x)<0 → cóncava hacia
abajo
8.-Asintotas.
Dom f(x) = R
Rgo f(x) = R
Pto de Corte con el eje X
Pto de Corte con el eje Y
(1;0)
(0,-4)
2
F´(x) = 3x -2x+4
0 = 3x2-2x+4 entonces las raices son x1c= 1/3+1.1i y x2c =
1/3-1.1 (son imaginarias) No son reales
− ∞,+∞ crece
(
)
Máximo : (xc, f(xc))
Máx.: No posee-no existen
Mínimo: ( xc , f(xc))
Min : No posee -no hay
f´´(x)=6x-2
0 = 6x-2 → x=1/3=0.33..
Coordenada del pto. de
inflexión
(0.33 ; -2.77 )
(− ∞,1 / 3] cóncava hacia
[1 / 3,+∞ )
abajo
Cóncava hacia arriba
No presenta asintotas
Con la información anterior se procede a graficar la función
Lcdo. Eliezer Montoya
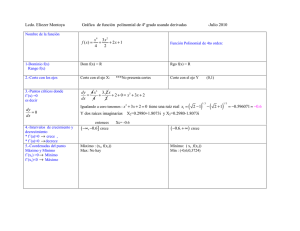
5).f(x) = x4- 6x2
Matemática I
13
+ 2 (polinomio de cuarto orden)
Nombre de la función
4
f(x) = x
-6 x2 +2
Bicuadratica o Polinomial:
Y = x^4-6x^2+2
1-Dominio f(x)
Rango f(x)
2.-Corte con los ejes
3.-Puntos críticos donde
f´(x) =0
Dom f(x) = R
Rgo f(x) = R
Pto de Corte con el eje X
Pto de Corte con el eje Y
(-2.39;0) ; (-0.59;0) , (0.59;0) (0,2)
y (2.39;0)
F´(x) = 4x3-12x = 2x.(2x2-6)
0 =4x3-18x = 2x.(2x2-9) entonces las raíces son x1c= 0 ;
x2c =
3 = ±1.73
4.-Intervalos de crecimiento y
decrecimiento
* f´(a)>0 → crece ,
* f´(a)<0 → decrece
[− 3;0] crece
[ 3;+∞) crece
(− ∞,− 3 ] decrece
[0; 3 ] decrece
5.-Coordenadas del punto
Máximo y Mínimo
f´(xc) >0 → Minimo
f´(xc)<0 → Maximo
6.-Puntos de inflexión
f´´(x) = 0
Máximo : (xc, f(xc))
Máx.: (0,2)
Mínimo: ( xc , f(xc))
Min : (1.73;-7) y (-173;-7)
7.- Concavidad:
f´´(x)>0 → cóncava hacia
arriba
f´´(x)<0 → cóncava hacia
abajo
8.-Asintotas.
[− 1,1] cóncava hacia abajo
2
f´´(x)=12x -12
2
0 =12x -12
→ x= 1 = ±1 ..
Coordenada del pto. de
inflexión
(+1 ; -3 ) y (-1,-3)
(− ∞,−1 Cóncava hacia
arriba
1,+∞ ) Cóncava hacia arriba
]
[
No presenta asintotas
Con la información anterior se procede a graficar la función
Lcdo. Eliezer Montoya
Matemática I
14
6) f(x)= ( x2 + 5x + 4 )( x2 - 4x + 3 )
Nombre de la función
1-Dominio f(x)
Rango f(x)
2.-Corte con los ejes
3.-Puntos críticos donde
f´(x) =0
4.-Intervalos de crecimiento y
decrecimiento
* f´(a)>0 → crece ,
* f´(a)<0 → decrece
f(x) = ( x2 + 5x + 4) * (x24x+3) = x4 + x3-13x2-x+12
Dom f(x) = R
Función Polinomial:
Y = (x^2+5x+4).(x^24x+3).
Rgo f(x) = R
Pto de Corte con el eje X
Pto de Corte con el eje Y
(-4;0) ; (-1;0) , (1;0) y (3;0)
(0,12)
F´(x) =( 2x+5)((x2-4x+3) + (2x-4) ( x2 + 5x + 4) = 4x3+3x226x-1 =0
entonces las raíces son x1c=-0.05 ; x2c =-2.92 y x3c =
2.22
(− ∞,−2.92 decrece
− 2.92;−0.05 crece
[
]
]
[2.22;+∞ ) crece
[− 0.05;2.22]
5.-Coordenadas del punto
Máximo y Mínimo
f´(xc) >0 → Minimo
f´(xc)<0 → Maximo
6.-Puntos de inflexión
f´´(x) = 0
Máximo : (xc, f(xc))
Máx.: (-0.05 ;12.01)
Mínimo: ( xc , f(xc))
Min : (-2.92;-48.1) y
2.22 ; -19.1)
Coordenada del pto. de
inflexión
(1.23 ; -4.6 ) y (-1.75,-22)
7.- Concavidad:
f´´(x)>0 → cóncava hacia
arriba
f´´(x)<0 → cóncava hacia
abajo
f´´(x)=12x2+6x-26
0 =12x2+6x-26
2
0 =6x +3x-13 →
x1 =1.23 y x2=1.75
− 1.75;1.23 cóncava hacia
abajo
[
8.-Asintotas.
]
decrece
(-
(− ∞,−1.75] Cóncava hacia
arriba
[1.23;+∞) Cóncava hacia
arriba
No presenta asintotas
Con la información anterior se procede a graficar la función
Lcdo. Eliezer Montoya
Matemática I
15
Lcdo. Eliezer Montoya
Matemática I
Con un zoom acercando los valores en un intervalo pequeños vemos
16
Lcdo. Eliezer Montoya
Matemática I
17
7) f(x) = x4 - 4x +2
Nombre de la función
f(x) = x4 -4x+2
Función Polinomial:
Y = x^4-4x+2
1-Dominio f(x)
Rango f(x)
2.-Corte con los ejes
3.-Puntos críticos donde
f´(x) =0
4.-Intervalos de crecimiento y
decrecimiento
* f´(a)>0 → crece ,
* f´(a)<0 → decrece
5.-Coordenadas del punto
Máximo y Mínimo
f´(xc) >0 → Minimo
f´(xc)<0 → Maximo
6.-Puntos de inflexión
f´´(x) = 0
7.- Concavidad:
f´´(x)>0 → cóncava hacia
arriba
f´´(x)<0 → cóncava hacia
abajo
8.-Asintotas.
Dom f(x) = R
Rgo f(x) = R
Pto de Corte con el eje X
Pto de Corte con el eje Y
(0.51;0) ; (1.36;0)
(0,2)
F´(x) = 4x3-4
0=4x3-4 entonces las raíces son x1c=1
1;+∞ crece
− ∞,1 decrece
[
)
(
]
Máximo : (xc, f(xc))
Máx.: no existe
Mínimo: ( xc , f(xc))
Min : (1;-1)
f´´(x)=12x2
0 =12x2
→ x=0
Coordenada del pto. de
inflexión
(0;2)
(− ∞,0] Cóncava hacia
arriba
[0;+∞ ) Cóncava hacia arriba
No presenta asintotas
Con la información anterior se procede a graficar la función
Lcdo. Eliezer Montoya
Matemática I
18
8) f ( x) = 4 − x 2 = ( 4 − x 2 )1 / 2 (semi- circunfencia)
Nombre de la función
2 1/2
f(x) = (4-x )
Función Irracional :
f:R → R Definida así:
f ( x ) = n P( x)
1-Dominio f(x)
Rango f(x)
2.-Corte con los ejes
3.-Puntos críticos donde
f´(x) =0
4.-Intervalos de crecimiento y
decrecimiento
* f´(a)>0 → crece ,
* f´(a)<0 → decrece
5.-Coordenadas del punto
Máximo y Mínimo
f´(xc) >0 → Minimo
f´(xc)<0 → Maximo
6.-Puntos de inflexión
f´´(x) = 0
Dom f(x) =
si n es par, la función tiene
restricciones P(x) ≥ 0
si n es impar no posee
restricciones (esta definida en
todo valor de X)
Rgo f(x) = 0;2
[− 2;2]
[ ]
Pto de Corte con el eje X
(-2;0) ; (2;0)
2x
F´(x) = −
2 4− x
2
=−
Pto de Corte con el eje Y
(0,2)
x
4 − x2
0 = x entonces los puntos críticos son x1c=0
− 2,0 crece
0,2 decrece
[
]
[ ]
Máximo : (xc, f(xc))
Máx.: (0,2)
Mínimo: ( xc , f(xc))
Min : No existen
f´´(x)=-4(4-x2)1/2
0 = -4(4-x2)1/2
Coordenada del pto. de
inflexión
(0;2)
→ x= ±2
7.- Concavidad:
f´´(x)>0 → cóncava hacia
arriba
f´´(x)<0 → cóncava hacia
abajo
8.-Asintotas.
[− 2,2] es cóncava hacia
abajo
En otro intervalo no esta
definida
No presenta asintotas
Con la información anterior se procede a graficar la función
En la grafica adjunta puedes
ver la en rojo la recta tangente
y como muestra su pendiente
cero ( la derivada en el punto
x=0)
Lcdo. Eliezer Montoya
Matemática I
19
En la grafica adjunta puedes
ver la en rojo la recta
tangente y como muestra su
pendiente positiva ( la
derivada en el punto x=1)
En la grafica adjunta puedes
ver la en rojo la recta
tangente y como muestra su
pendiente negativa ( la
derivada en el punto x=1)
**Recuerde la aplicación
de la recta tangente y
normal de una función en
el punto x = a
Lcdo. Eliezer Montoya
9) f ( x) =
Matemática I
20
x
x+3
Nombre de la función
f(x) = x/( x+3 )
Función Racional: f:R → R
Definida así:
P( x)
donde
Q( x)
Q ( x) ≠ 0
Rgo f(x) = R- {1}
f ( x) =
1-Dominio f(x)
Rango f(x)
Dom f(x) = R - {− 3}
El valor que anula a x+3 es 3 (este se excluye )
2.-Corte con los ejes
Pto de Corte con el eje X
(0,0)
3.-Puntos críticos donde
f´(x) =0
4.-Intervalos de crecimiento y
decrecimiento
* f´(a)>0 → crece ,
* f´(a)<0 → decrece
5.-Coordenadas del punto
Máximo y Mínimo
f´(xc) >0 → Mínimo
f´(xc)<0 → Máximo
6.-Puntos de inflexión
f´´(x) = 0
F´(x) =
x
x
=> 0=
2
( x + 3)
( x + 3) 2
0 = x entonces los puntos críticos son x1c=0
No posee intervalos de
− ∞,−3 crece
decrecimiento
(
)
(− 3,+∞ ) crece
Máximo : (xc, f(xc))
Máx.: No tiene
f´´(x)=
0=
− x2 + 9
( x + 3) 4
− x2 + 9
( x + 3) 4
→ x=
7.- Concavidad:
f´´(x)>0 → cóncava hacia
arriba
f´´(x)<0 → cóncava hacia
abajo
8.-Asíntotas.
f(x)= y y su inversa es f(y)=x
donde x= 3y/(y-1) el valor
que anula a y-1 es 1 (este se
excluye del rango)
Pto de Corte con el eje Y
(0,0)
Mínimo: ( xc , f(xc))
Min : No existen
Coordenada del pto. de
inflexión
Para x=-3 no esta definida
9 = ±3
Asíntota Horizontal
Y= 1 es una asíntota
horizontal ya que :
lim f ( x) = 1 y también
x → +∞
lim f ( x) = 1
x → −∞
Con la información anterior se procede a graficar la función
Asíntota Vertical
X=3 es una asíntota vertical
ya que:
lim f ( x) = −∞ y
x →3+
lim
x→ 3+
f (x) = ∞
Lcdo. Eliezer Montoya
Matemática I
En rojo podemos ver la asíntota vertical (el valor que se excluye del dominio)
21
Lcdo. Eliezer Montoya
10) f ( x) =
Matemática I
22
x−2
x − .5
Nombre de la función
f(x) = (x-2) / ( x-5 )
Función Racional: f:R → R
Definida así:
P( x)
donde
Q( x)
Q ( x) ≠ 0
Rgo f(x) = R- {1}
f ( x) =
1-Dominio f(x)
Rango f(x)
Dom f(x) = R - {5}
El valor que anula a x-5 es 5
(este se excluye )
2.-Corte con los ejes
Pto de Corte con el eje X
(2,0)
3.-Puntos críticos donde
f´(x) =0
4.-Intervalos de crecimiento y
decrecimiento
* f´(a)>0 → crece ,
* f´(a)<0 → decrece
5.-Coordenadas del punto
Máximo y Mínimo
f´(xc) >0 → Minimo
f´(xc)<0 → Maximo
6.-Puntos de inflexión
f´´(x) = 0
7.- Concavidad:
f´´(x)>0 → cóncava hacia
arriba
f´´(x)<0 → cóncava hacia
abajo
8.-Asíntotas.
F´(x) =
f(x)= y ; su inversa es f(y)=x
donde despejando
x=( 5y-2)/(y-1) el valor que
anula a y-1 es 1 (este se
excluye del rango)
Pto de Corte con el eje Y
(0,2/5) =(0;0.4)
−3
−3
=> 0=
2
( x − 5)
( x − 5) 2
No posee.
No posee intervalos de
crecimiento
(− ∞,5) decrece
(5,+∞ )
decrece
Máximo : (xc, f(xc))
Máx.: No tiene
Mínimo: ( xc , f(xc))
Min : No existen
6
( x − 5) 3
6
0=
( x − 5) 3
Coordenada del pto. de
inflexión
f´´(x)=
No existen
No hay
Asíntota Horizontal
Y= 1 es una asíntota
horizontal ya que :
lim f ( x) = 1 y también
x → +∞
lim f ( x) = 1
x → −∞
Con la información anterior se procede a graficar la función
Asíntota Vertical
X=5 es una asíntota vertical
ya que:
lim f ( x) = +∞ y
x →5 +
lim f ( x) = −∞
x →5 −
Lcdo. Eliezer Montoya
En azul la función
f ( x) =
Matemática I
x−2
−3
y en verde su derivada f´(x)=
x − .5
( x − 5) 2
23
Lcdo. Eliezer Montoya
11) f ( x) =
Matemática I
24
x+2
x − .2
Nombre de la función
f(x) = (x+2) / ( x-2 )
Función Racional: f:R → R
Definida así:
P( x)
donde
Q( x)
Q ( x) ≠ 0
Rgo f(x) = R- {1}
f ( x) =
1-Dominio f(x)
Rango f(x)
Dom f(x) = R - {2}
El valor que anula a x-2 es 2
(este se excluye del dominio
)
2.-Corte con los ejes
Pto de Corte con el eje X
(-2,0)
3.-Puntos críticos donde
f´(x) =0
4.-Intervalos de crecimiento y
decrecimiento
* f´(a)>0 → crece ,
* f´(a)<0 → decrece
5.-Coordenadas del punto
Máximo y Mínimo
f´(xc) >0 → Minimo
f´(xc)<0 → Maximo
6.-Puntos de inflexión
f´´(x) = 0
7.- Concavidad:
f´´(x)>0 → cóncava hacia
arriba
f´´(x)<0 → cóncava hacia
abajo
8.-Asíntotas.
F´(x) =
f(x)= y ; su inversa es f(y)=x
donde despejando
x=( y+2)/(y-1) el valor que
anula a y-1 es 1 (este se
excluye del rango)
Pto de Corte con el eje Y
(0,-1)
−3
−3
=> 0=
2
( x − 5)
( x − 5) 2
No posee.
No posee intervalos de
crecimiento
(− ∞,2) decrece
(2,+∞ )
decrece
Máximo : (xc, f(xc))
Máx.: No tiene
Mínimo: ( xc , f(xc))
Min : No existen
8
( x − 2) 3
8
0=
( x − 2) 3
Coordenada del pto. de
inflexión
f´´(x)=
No existen
No hay
Asíntota Horizontal
Y= 1 es una asíntota
horizontal ya que :
lim f ( x) = 1 y también
x → +∞
lim f ( x) = 1
x → −∞
Con la información anterior se procede a graficar la función
Asíntota Vertical
X=2 es una asíntota vertical
ya que:
lim f ( x) = +∞ y
x →2+
lim f ( x) = −∞
x →2−
Lcdo. Eliezer Montoya
Matemática I
25