TALLER 1 UNIDAD 3 HIPERTEXTOS 10 GRAFICA DE FUNCIONES TRIG

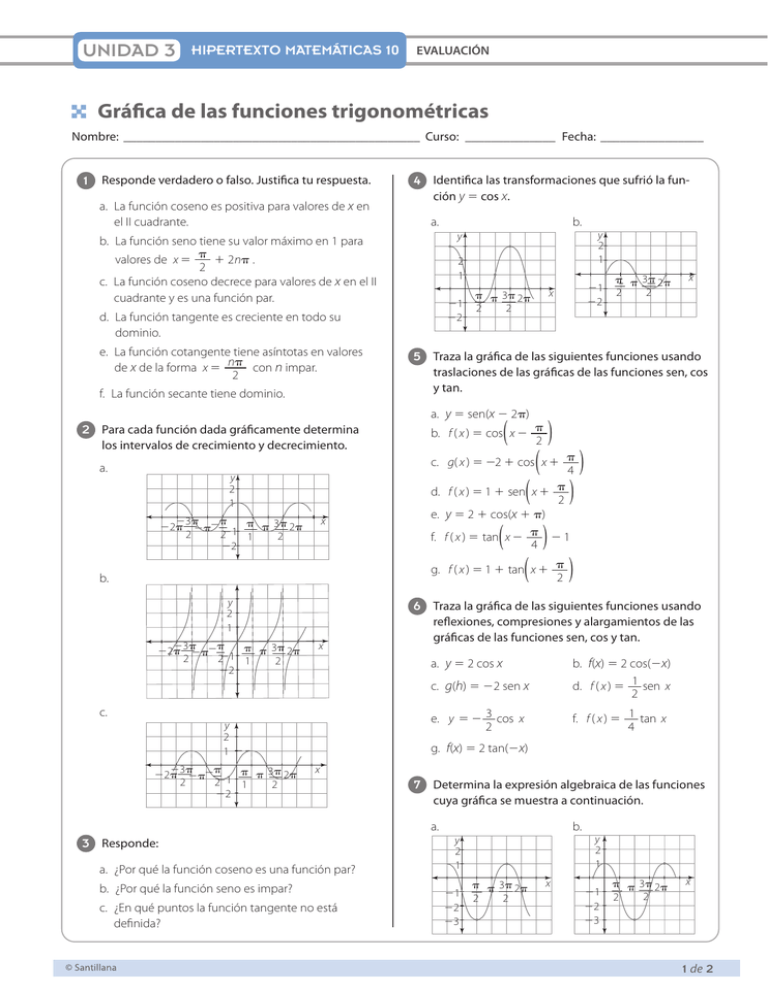
UNIDAD 3
HIPERTEXTO MATEMÁTICAS 10
EVALUACIÓN
Gráfica de las funciones trigonométricas
Nombre:_ ______________________________________________ Curso:_ ______________ Fecha:_ ________________
1 Responde verdadero o falso. Justifica tu respuesta.
a. La función coseno es positiva para valores de x en
el II cuadrante.
b. La función seno tiene su valor máximo en 1 para
valores de x 2 n .
2
c. La función coseno decrece para valores de x en el II
cuadrante y es una función par.
d. La función tangente es creciente en todo su
dominio.
e. La función cotangente tiene asíntotas en valores
de x de la forma x n con n impar.
2
f. La función secante tiene dominio.
4 Identifica las transformaciones que sufrió la función y 5 cos x.
a. b.
2
1
1
2
los intervalos de crecimiento y decrecimiento.
a.
x
3
2 1 3 2
2
2
2
1
2
y
2
1
3
2 1 3 2
2
2
2
1
2
(
b. f ( x ) cos x 2
(
)
c. g( x ) 2 cos x 4
d. f ( x ) 1 sen x 2
e. y 5 2 1 cos(x 1 p)
f. f ( x ) tan x 1
4
(
(
)
)
x
)
reflexiones, compresiones y alargamientos de las
gráficas de las funciones sen, cos y tan.
a. y 5 2 cos x
b. f(x) 5 2 cos(2x)
d. f ( x ) 5 1 sen x
2
e. y 3 cos x
2
y
2
1
3
2 1 3 2
2
2
2
1
2
)
6 Traza la gráfica de las siguientes funciones usando
c. g(h) 5 22 sen x
c.
x
traslaciones de las gráficas de las funciones sen, cos
y tan.
g. f ( x ) 1 tan x 2
b.
3 2
2
2
5 Traza la gráfica de las siguientes funciones usando
(
y
2
1
1
2
x
3 2
2
2
a. y 5 sen(x 2 2p)
2 Para cada función dada gráficamente determina
y
2
1
y
f. f ( x ) 5 1 tan x
4
g. f(x) 5 2 tan(2x)
x
7 Determina la expresión algebraica de las funciones
cuya gráfica se muestra a continuación.
a. b.
3 Responde:
a. ¿Por qué la función coseno es una función par?
b. ¿Por qué la función seno es impar?
c. ¿En qué puntos la función tangente no está
definida?
y
2
1
1
2
3
3 2
2
2
x
y
2
1
1
2
3
3 2
2
2
x
1 de 2
UNIDAD 3
HIPERTEXTO MATEMÁTICAS 10
8 Identifica el período, la amplitud y el desfase de las
siguientes funciones.
a. y 5 22 cos(x 2 p)
(
)
b. y 1 sen x 2
4
c. y 5 3 cos(x 2 p)
(
)
d. y 4 sen x 3
2
(
)
EVALUACIÓN
13 Encuentra el valor del ángulo u a partir de los valores de los lados.
e. y 3 tan x 2
f. y 1 sen x 3
4
2
g. y 1 cot x 3
2
(
(
h. y 5 22 sec(x 2 p)
9 Para la función y 5 2 cos21 x determina:
a. Gráfica
)
)
2,3
1,3
14 Resuelve:
a. Un niño eleva una cometa, cuando lleva 30 m de
pita la cometa ha alcanzado una altura de 20 m.
¿Cuál es el ángulo de elevación de la cometa?
b. Dominio
c. Rango
30 m
d. Intervalos de crecimiento.
e. Intervalos donde la función es positiva.
20 m
x
10 Para la función y = 1 + 1 sen-1 x determina:
2
a. Gráfica
b. Dominio
c. Rango
d. Intervalos de crecimiento.
e. Intervalos donde la función es positiva.
b. Un faro alumbra un bote pesquero que está a
200 m del faro. Si la distancia del bote a la punta
del faro es de 500 m, ¿cuál es el ángulo que forma
el destello del luz con el faro?
11 Determina el valor de cada función inversa.
a. tan21
( 3 )
(
b. sen21 2
( )
2
2
500 m
)
c. cos21 1 2
d. cos21
( )
2
2
( )
f. csc21 (2 2 )
e. cot21 2 3
12 Despeja x en cada expresión.
a. y 5 2 sen 3x
b. y 1 sen( x )
2
( )
c. y 5 cos -1 x
2
d. y 5 tan (cos21 2x)
x
200 m
c. Un objeto pende de un resorte, el movimiento de
este está representado mediante la ecuación
y 5 5 sen 2pt, donde t se mide en segundos y y
en centímetros. Encuentra la amplitud y el período
del movimiento del objeto. Realiza la gráfica de la
función.
d. El movimiento de un péndulo se describe
mediante la función y 5 10 cos 4pt. Encuentra la
amplitud del movimiento y realiza la gráfica.
e. Una partícula registra un movimiento
armónico simple descrito por la ecuación
y 1 sen 2t . Determina la amplitud del
2
2
movimiento, el período y el desplazamiento.
(
)
2 de 2