Ecs recta 2D 170809 261210 1558
Anuncio
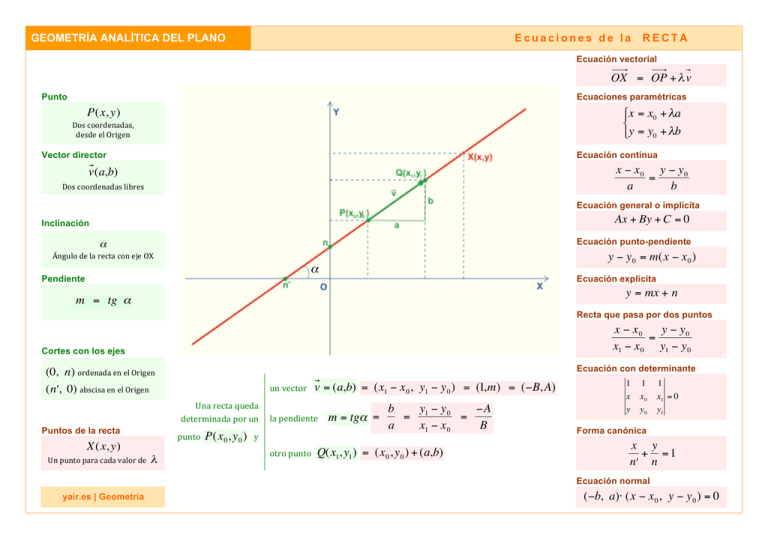
€ € GEOMETRÍA ANALÍTICA DEL PLANO Ecuaciones de la RECTA Ecuación vectorial OX = OP + λ v Punto Ecuaciones paramétricas P(x, y) Dos coordenadas, desde el Origen ⎧x = x0 + λa ⎨ ⎩y = y0 + λb € Vector director € Ecuación contínua x − x0 y − y0 = a b v(a,b) € Dos coordenadas libres Ecuación general o implícita Ax + By + C = 0 € Inclinación € α Ecuación punto-pendiente Ángulo de la recta con eje OX y − y 0 = m(x − x 0 ) α Pendiente € € y = mx + n m = tg α € € € un vector v Una recta queda determinada por un Puntos de la recta punto P(x 0 , y 0 ) y X(x, y) Un punto para cada valor de λ yair.es | Geometría € x − x0 y − y0 = x1 − x 0 y1 − y 0 Ecuación con determinante (0, n) ordenada en el Origen ( nʹ′, 0) abscisa en el Origen € Recta que pasa por dos puntos € Cortes con los ejes Ecuación explícita € = (a,b) = (x1 − x 0 , y1 − y 0 ) = (1,m) = (−B, A) la pendiente m € = tgα = b y − y0 −A = 1 = a x1 − x 0 B € otro punto Q(x1, y1 ) = (x 0 , y 0 ) + (a,b) € € € € 1 x y € 1 x0 y0 1 x1 = 0 y1 Forma canónica € x y + =1 nʹ′ n Ecuación normal (−b, a)⋅ (x − x 0 , y − y 0 ) = 0 €