sep 07 sol
Anuncio

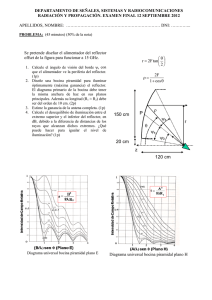
DEPARTAMENTO DE SEÑALES, SISTEMAS Y RADIOCOMUNICACIONES RADIACIÓN Y PROPAGACIÓN. EXAMEN FINAL 14 SEPTIEMBRE 2007 TEORÍA: (40% de la nota) Instrucciones: responda de manera breve y concisa, en el espacio asignado, a cada pregunta. No es necesario realizar ningún cálculo No está permitido utilizar calculadora. 1. Para un radioenlace de 10 GHz por onda de superficie se emplean antenas de tipo monopolo… Señale las dos incongruencias que hay en la frase anterior. (0.4p) - A 10 GHz la onda de superficie, si se excitase, no llegaría ni a 1 metro. - A 10 GHz, para radioenlaces, se utilizan antenas de alta ganancia, y el monopolo no lo es. 2. ¿Cuál es la temperatura de ruido típica de las antenas embarcadas en satélite para el servicio de radiodifusión de televisión? (0.4p) Alrededor de 290K, que es la temperatura de brillo de la Tierra, a la que “ven” las antenas embarcadas en satélite a través de sus diagramas. 3. Una antena Yagi tiene una ganancia de 14 dBi. ¿Es esto posible? (0.4p) Sí, con unos cuantos elementos directores. (Las ganancias pueden dar ganancias entre 7 y unos 17-18 dBi, según el número de directores) 4. ¿Por qué se utilizan los balunes para alimentar las antenas de tipo dipolo? (0.4p) Para asegurar la simetría de la corriente en los brazos del dipolo, y evitar la corriente externa sobre el cable coaxial de alimentación, que genera entre otras cosas radiación contrapolar. 5. ¿Qué propiedades eléctricas hacen atractivas las hélices radiando en el modo axial? (0.4p) Gran ancho de banda con buena adaptación de impedancias (e impedancia de entrada real), haz tipo pincel según el eje, ganancias medias y polarización circular. 6. ¿Qué le ocurre a un array endfire si la separación entre elementos es λ/2? (0.4p) Que se hace bidireccional por la aparición del “grating lobe” (en este caso lóbulo idéntico al deseado) que aparece en la dirección opuesta al lóbulo principal. 7. En las modernos arrays de estaciones base de telefonía móvil de tilt (apuntamiento) variable, ¿cómo se controla la dirección de apuntamiento del haz, manteniendo fija la antena? (0.4p) Variando el desfasaje progresivo entre elemento, cambiando por ejemplo la longitud eléctrica desde la puerta de entrada hasta cada elemento. 8. Entre dos bocinas piramidales con la misma apertura, una óptima y otra de bajo error de fase, ¿cuál tiene mayor ganancia y cuál es más larga? (0.4p) La de bajo error de fase es más larga y da más ganancia porque su diagrama tiene lóbulos más bajos, no tiene rellenos de nulos y haz más estrecho (ver diagramas universales). 9. ¿Qué se consiguen con las corrugaciones en las bocinas cónicas corrugadas respecto a las bocinas cónicas lisas? (0.4p) Las corrugaciones anulan las corrientes longitudinales dentro de la bocina transformando el modo TE11 a HE11, con líneas de campo paralelas en la apertura y campo nulo en toda su periferia. Esto iguala los diagramas copulares (Plano E y Plano H), dando una radiación contrapolar muy baja. 10. Diga qué ocurre a la ganancia, eficiencias, ancho de haz y nivel de lóbulo lateral, cuando a una Cassegrain centrada iluminada para máxima ganancia se le sustituye la bocina de iluminación de bajo error de fase por otra de menor diámetro (también de bajo error de fase). (0.4p) La ganancia baja, al perderse la iluminación óptima. Como la bocina es menos directiva y tiene una haz más ancho, la apertura del reflector queda iluminada más uniformemente. Entonces, la eficiencia de apertura aumenta y la de spillover se reduce (la global se reduce también). Además el ancho de haz se reduce ligeramente y el nivel de lóbulos secundarios sube. DEPARTAMENTO DE SEÑALES, SISTEMAS Y RADIOCOMUNICACIONES RADIACIÓN Y PROPAGACIÓN. EXAMEN FINAL 14 SEPTIEMBRE 2007 APELLIDOS, NOMBRE: ………………………………………………………… DNI: ………….. PROBLEMA 1: (30% de la nota) Se dispone de dos bocinas piramidales óptimas de banda C (f=5 GHz) con aperturas de A=24 cm x B=18 cm. Se dispone también de un amplificador de la misma banda que da una figura de ruido al sistema de 1.4 dB. Se trata de diseñar un radioenlace para transmisión de video de 10 MHz de ancho banda para comunicar las orillas de un lago de 12 km de ancho. 1. Calcule la altura óptima de las torres (supuestas iguales) para situar las bocinas. 2. Calcule la potencia disponible necesaria del transmisor para conseguir una S/N=26 dB, para el caso peor de lluvia torrencial de 100 litros/hora que produce una temperatura de ruido de antena en sentido horizontal de 220 K (k=1.38 10-23 W/Hz/K) Atenuación por lluvia(dB/km) SOLUCIÓN: 1. La altura óptima es la que consigue que el rayo directo y el rayo reflejado se sumen en fase. La suma vectorial de los dos rayos se presenta en la expresión siguiente. En dicha expresión, el coeficiente de reflexión en el suelo (agua del lago) es igual a -1, y para que se sumen en fase los dos rayos el exponente tiene que ser jnπ, con n impar. La altura óptima será la mínima, que se obtiene para el menor valor del mismo, es decir, para n=1. ( ) ( ) r r r r r E total = E d + E r = E d ⋅ 1 + ρ ⋅ e − jk o ∆d = E d ⋅ 1 − e − jk o ∆d ⇒ jk o ∆d = jnπ = jπ La diferencia de caminos, por lo tanto tiene que ser : ∆d = λ 2 = 3cm Esta diferencia de caminos se puede calcular geométricamente como: ∆d = d 2 + 4h 2 − d = λ 2 = 3cm ⇒ d = 13.41m Siendo d=12000 metros. 2. Para calcular la potencia disponible necesaria del transmisor se tiene que aplicar la fórmula de Friis. Para ello, comenzamos calculando cuál será la potencia entregada al receptor, utilizando la relación S/N y calculando el nivel de ruido: Prx (dBm) = S / N(dB) + N(dBm) = 26dB + 10 log kBT = 26dB + 10 log kB(Ta + To ⋅ (f − 1) )) = −77.4dBm Donde, k=1.38 10-20 mW/Hz/K, para poder trabajar en dBm, B=107 Hz, Ta=220K, To=290K y f=101.4/10 Una vez se ha calculado la potencia recibida, la potencia transmitida se puede calcular aplicando la fórmula de Friis, considerando que hay acoplo perfecto de polarización y no hay pérdidas por desapuntamiento: Prx (dBm) = −77.4dBm = Ptx (dBm) + G ant , tx − 20 log 4πd + G ant ,rx + Frefl − L lluvia λ Donde los distintos factores se calculan como: - La ganancia de la antena transmisora es igual a la ganancia de la antena receptora. Sabiendo que la eficiencia de apertura es 0.5 (por ser bocina óptima), se tiene: 4π ⎛ 4π ⎞ ⎞ ⎛ G ant , tx = G ant ,rx = 10 log⎜ ε a 2 A ant ⎟ = 10 log⎜ 0.5 24cm ⋅ 18cm ⎟ = 18.8dBi 6cm ⋅ 6cm ⎝ λ ⎠ ⎝ ⎠ - El efecto de la reflexión hace que se doble el campo total, ganando en potencia 20log2=6dB El efecto de la lluvia, se puede mirar en la gráfica de 100litros/hora = 100mm/hora. A la frecuencia de 5 GHz, se tiene una atenuación de 0.25 dB/km, que para 12 km son 3 dB. Las pérdidas de espacio libre para d=12000 metros y λ=0.06 metros, se tienen 128 dB Despejando la potencia transmitida, se tiene un valor de 10 dBm, que son 10 mW. PROBLEMA 2: (30% de la nota) Una hélice de banda S (frecuencia = 3 GHz) que radia en modo axial genera sobre el eje z a una distancia de 20 metros un campo con una amplitud compleja de x̂ + j1.2 ŷ V/m cuando se le alimenta con 1 W de potencia. 1. Calcule la ganancia de la hélice. 2. Calcule la potencia disponible en bornes de esta hélice (funcionando en recepción) cuando incide sobre ella un campo linealmente polarizado según el eje y de 1V/m que viene de una antena lejana situada sobre el eje z. SOLUCIÓN: 1. Para el cálculo de la ganancia de la hélice, partimos de la definición de la ganancia de una antena: G ant ⎡ 12 + 1.2 2 ⎢ ⎡ S ⎤ 2η o 2 2 = 10 log ⎢4πr ⎥ = 10 log ⎢4π20 ⎢ PET ⎦ 1W ⎣ ⎢ ⎣ ⎤ ⎥ ⎥ = 10 log 16.26 = 12.1dBi , con ηo=120π. ⎥ ⎥ ⎦ 2. Para el cálculo de la potencia disponible en bornes de la hélice, aplicamos la expresión: PDR = 10 log[FPP ⋅ A e ⋅ S i ] = −50dBW = −20dBm , donde: x̂ + j1.2 ŷ = ⋅ ŷ = 0.59 1.56 2 - El factor de pérdidas de polarización se calcula como: FPP = ê T ⋅ ê R - La densidad de potencia incidente, para una campo de 1 V/m es: S i = - El área equivalente de la hélice: A e = 2 r2 E 2η o λ2 0 .1 2 G ant = 16.26 = 0.0129m 2 4π 4π =1 240π = 1.33mW / m 2