sol sept 12

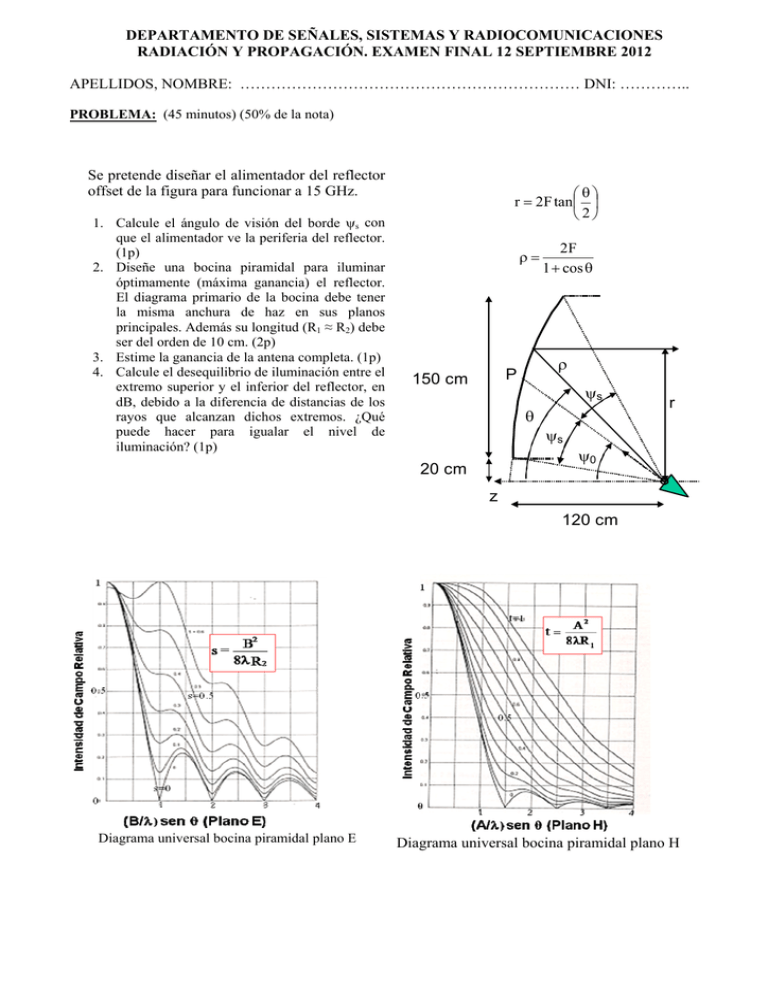
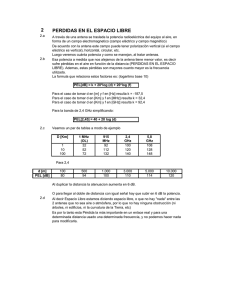
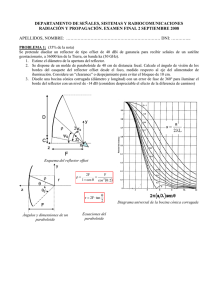
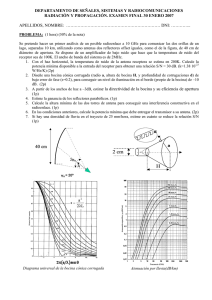
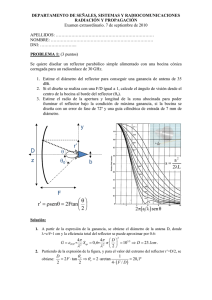
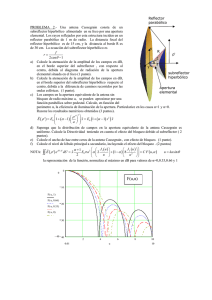
DEPARTAMENTO DE SEÑALES, SISTEMAS Y RADIOCOMUNICACIONES
RADIACIÓN Y PROPAGACIÓN. EXAMEN FINAL 12 SEPTIEMBRE 2012
APELLIDOS, NOMBRE: ………………………………………………………… DNI: …………..
PROBLEMA: (45 minutos) (50% de la nota)
Se pretende diseñar el alimentador del reflector
offset de la figura para funcionar a 15 GHz.
1. Calcule el ángulo de visión del borde s con
que el alimentador ve la periferia del reflector.
(1p)
2. Diseñe una bocina piramidal para iluminar
óptimamente (máxima ganancia) el reflector.
El diagrama primario de la bocina debe tener
la misma anchura de haz en sus planos
principales. Además su longitud (R1 ≈ R2) debe
ser del orden de 10 cm. (2p)
3. Estime la ganancia de la antena completa. (1p)
4. Calcule el desequilibrio de iluminación entre el
extremo superior y el inferior del reflector, en
dB, debido a la diferencia de distancias de los
rayos que alcanzan dichos extremos. ¿Qué
puede hacer para igualar el nivel de
iluminación? (1p)

r  2F tan 
2


P
150 cm
2F
1  cos 
s

r
s
0
20 cm
z
120 cm
Diagrama universal bocina piramidal plano E
Diagrama universal bocina piramidal plano H
Solución:

1. Aplicamos la expresión r  2F tan  para los extremos superior e inferior del paraboloide,
2
obteniendo:
  s 
20  2  120 tan o
   o   s  9.53º
2


   s 
170  2  120 tan o
   o   s  70.62º
2


Operando: s=30.5º
2. Por la longitud de la bocina vamos a partir de valores de errores de fase en cada plano, t = s =0.
En el ángulo calculado anteriormente, s=30.5º, tenemos un nivel de -10 dB, que corresponden a
10-10/20=0.32, para conseguir iluminar el reflector de manera óptima. Con estos valores, cortamos
en las gráficas en los valores de abcisas:
PlanoE :
B

PlanoH :
sin s  0.7  B  2.76cm
A

sin s  1  A  3.94cm
Con estos valores, recalculamos los errores de fase:
B2
A2
 0.05 ; t 
 0.1
8R2
8R1
Que son suficientemente bajos para ser considerada bocina de bajo error de fase.
s
3. La ganancia se estima a partir de una eficiencia total igual a 0.7:
G  10 log 
4

2
R 2  10 log 0.7
4
 75 2  45.9dBi
2
2
4. El desequilibrio de amplitud se calcula a partir de la propagación esférica de la onda asociada al
tramo que va desde el alimentador hasta los dos extremos del paraboloide.
2F
 sup
1  cos o   s 
 20 log
20 log
 3.5dB
2F
 sup
1  cos o   s 
Se puede corregir cambiando el apuntamiento del alimentador, haciendo que éste apunte hacia
arriba (menor nivel) para compensar el valor de 3.5 dB.
DEPARTAMENTO DE SEÑALES, SISTEMAS Y RADIOCOMUNICACIONES
RADIACIÓN Y PROPAGACIÓN. EXAMEN FINAL 12 SEPTIEMBRE 2012
APELLIDOS, NOMBRE: ………………………………………………………… DNI: …………..
TEORÍA: (40 minutos) (50% de la nota)
Instrucciones: responda de manera breve y concisa, en el espacio asignado, a cada pregunta.
1. ¿Durante qué fase del día (día o noche) típicamente se produce zona de sombra en torno a una antena de
HF a la frecuencia de 5 MHz? Explique por qué. (0.5p)
De noche baja la densidad de electrones y por tanto la frecuencia crítica, ya que ésta es f c  9 N max . Esta
frecuencia crítica se sitúa por debajo de 5 MHz, dando lugar a que los rayos próximos a la incidencia
vertical se escapen hacia el exterior, produciéndose una zona de sombra.
2. Para un sistema de radiodifusión en onda media por onda de superficie (1 MHz) se emplea un dipolo
resonante horizontal situado a 30 metros de altura... Comente qué no funciona en este sistema de
radiodifusión. (0.5p)
La polarización horizontal no se puede propagar por onda de superficie.
3. Para un radioenlace terrestre de 30 km, a partir de qué frecuencia es importante la atenuación por lluvia
intensa. (0.5p)
A partir de 3 GHz.
4. ¿Cuál es el margen de temperaturas típicas de las antenas Cassegrain de estaciones terrenas de
comunicaciones por satélite (para ángulos por encima de 20º sobre el horizonte) en banda C (4-6 GHz)?
(0.5p)
Depende del diseño de la antena Cassegrain, pero está en torno a 40K.
5. ¿Qué ganancia típica se puede obtener con una bocina piramidal óptima a 10 GHz de 9cm x 6cm de
apertura? (0.5p)
Las bocinas óptimas tienen una eficiencia de apertura de 0.5. Considerando eficiencia de radiación 1, tenemos:
G  10 log  a
4

2
AB  10 log 0.5
4
9  6  15.8dBi
32
6. ¿Qué condiciones debe cumplir la geometría de una hélice para radiar en el modo axial? (0.5p)
Las condiciones básicas para la geometría de una hélice en modo axial son perímetro (2R) del orden de la
longitud de onda, y un ángulo de enrollamiento de en torno a 12º.
7. Si se diseña un array con una excitación que reduce el nivel de lóbulos secundarios respecto al caso de
iluminación uniforme, ¿qué ocurre con la directividad y la anchura de haz entre puntos de potencia mitad?
(0.5p)
Para reducir el nivel de lóbulos secundarios se tiene una excitación decreciente del centro hacia el borde. Con
esta excitación se reduce la directividad y aumenta la anchura de haz entre puntos de potencia mitad.
8. Una antena que funciona a 3 GHz genera un campo radiante de 1V/m a 1 metro de distancia en la
dirección de máxima radiación, cuando se le entrega una potencia de 1mW.
a) Calcule la densidad de potencia a 50 metros de distancia. (0.5p)
El campo eléctrico es inversamente proporcional a la distancia con lo que a 50 metros tendremos un
2
2
E
1
 1 
 
 0.53W / m 2
campo de: 1/50 V/m. Para calcular la densidad de potencia: S 
2  50  2  120
b) Calcule la ganancia de la antena. (0.5p)
Para el cálculo de la ganancia: G 
4d 2 S
Pent
 16.65  10 log 16.65  12.2dBi
3  e  jko z
xˆ  jyˆ  , incide
9. Sobre una antena que en transmisión radia en la dirección del eje z un campo
z
proveniente de un punto lejano situado sobre el eje de las z positivas, un campo de 0.1x̂ V/m. La
ganancia de la antena en la dirección del eje z es de 10 dBi y funciona a una frecuencia de 1 GHz. Calcule
la potencia disponible en bornes de la antena. (0.5p)
Pdis  S Aef eˆt  eˆr
2

0.12 2
10  0.5  0.47mW
2  120 4