Feb. 2010

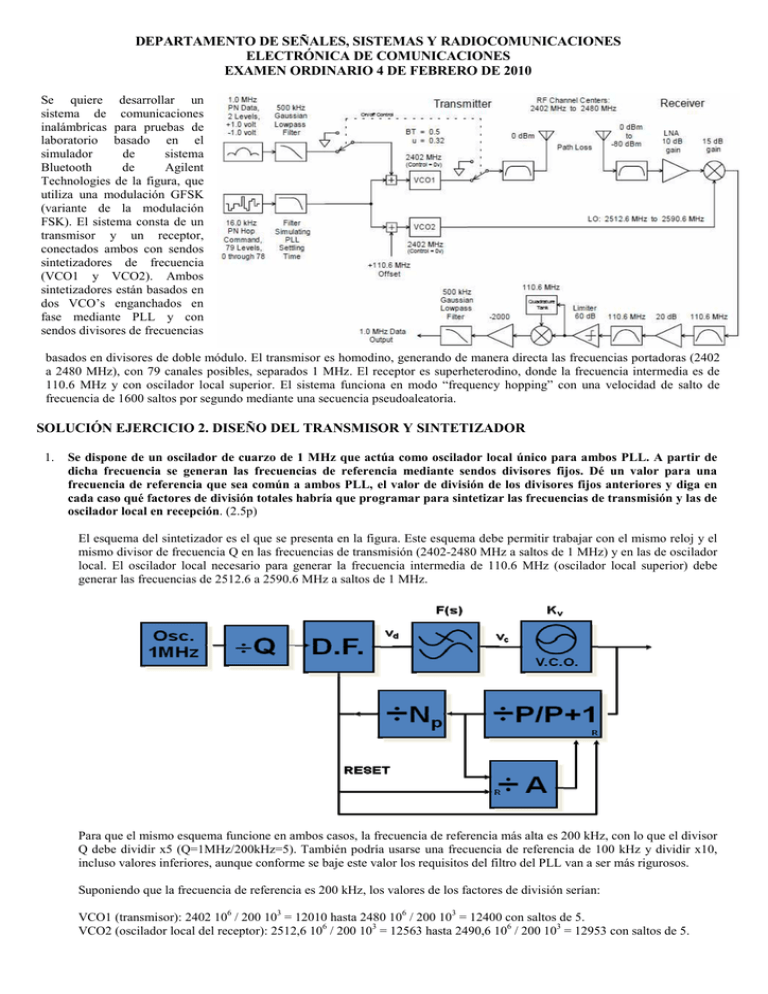
DEPARTAMENTO DE SEÑALES, SISTEMAS Y RADIOCOMUNICACIONES
ELECTRÓNICA DE COMUNICACIONES
EXAMEN ORDINARIO 4 DE FEBRERO DE 2010
Se quiere desarrollar un
sistema de comunicaciones
inalámbricas para pruebas de
laboratorio basado en el
simulador
de
sistema
Bluetooth
de
Agilent
Technologies de la figura, que
utiliza una modulación GFSK
(variante de la modulación
FSK). El sistema consta de un
transmisor y un receptor,
conectados ambos con sendos
sintetizadores de frecuencia
(VCO1 y VCO2). Ambos
sintetizadores están basados en
dos VCO’s enganchados en
fase mediante PLL y con
sendos divisores de frecuencias
basados en divisores de doble módulo. El transmisor es homodino, generando de manera directa las frecuencias portadoras (2402
a 2480 MHz), con 79 canales posibles, separados 1 MHz. El receptor es superheterodino, donde la frecuencia intermedia es de
110.6 MHz y con oscilador local superior. El sistema funciona en modo “frequency hopping” con una velocidad de salto de
frecuencia de 1600 saltos por segundo mediante una secuencia pseudoaleatoria.
SOLUCIÓN EJERCICIO 2. DISEÑO DEL TRANSMISOR Y SINTETIZADOR
1.
Se dispone de un oscilador de cuarzo de 1 MHz que actúa como oscilador local único para ambos PLL. A partir de
dicha frecuencia se generan las frecuencias de referencia mediante sendos divisores fijos. Dé un valor para una
frecuencia de referencia que sea común a ambos PLL, el valor de división de los divisores fijos anteriores y diga en
cada caso qué factores de división totales habría que programar para sintetizar las frecuencias de transmisión y las de
oscilador local en recepción. (2.5p)
El esquema del sintetizador es el que se presenta en la figura. Este esquema debe permitir trabajar con el mismo reloj y el
mismo divisor de frecuencia Q en las frecuencias de transmisión (2402-2480 MHz a saltos de 1 MHz) y en las de oscilador
local. El oscilador local necesario para generar la frecuencia intermedia de 110.6 MHz (oscilador local superior) debe
generar las frecuencias de 2512.6 a 2590.6 MHz a saltos de 1 MHz.
Para que el mismo esquema funcione en ambos casos, la frecuencia de referencia más alta es 200 kHz, con lo que el divisor
Q debe dividir x5 (Q=1MHz/200kHz=5). También podría usarse una frecuencia de referencia de 100 kHz y dividir x10,
incluso valores inferiores, aunque conforme se baje este valor los requisitos del filtro del PLL van a ser más rigurosos.
Suponiendo que la frecuencia de referencia es 200 kHz, los valores de los factores de división serían:
VCO1 (transmisor): 2402 106 / 200 103 = 12010 hasta 2480 106 / 200 103 = 12400 con saltos de 5.
VCO2 (oscilador local del receptor): 2512,6 106 / 200 103 = 12563 hasta 2490,6 106 / 200 103 = 12953 con saltos de 5.
2.
Diseñe el PLL sintetizador, basado en divisores de doble módulo que funcionan hasta 3 GHz, para poder generar las
frecuencias de transmisión y las de oscilador local del mezclador. Utilice divisores con P=8. ¿Sería factible utilizar
P=128 con el diseño realizado? (2.5p)
Tal como dice el enunciado P=8, con lo que A irá de 1 a 8 (también se considera válido el que haya puesto de 0 a 7).
Los valores de Np, calculados para los valores de división del apartado 1 son:
VCO1: Npmin = 1501 y Npmax = 1549
VCO2: Npmin = 1570 y Npmax = 1619
Con esta frecuencia de referencia no se podría utilizar P=128 porque Nmin > P2 + 1. Para usar P=128 habría que reducir la
frecuencia de referencia a 100 kHz (por ejemplo).
3.
Si se utiliza un esquema con ξ=0.7, calcule la pulsación propia para que el tiempo de conmutación sea de 180µ
µs.
Considere que la secuencia de hopping pseudoaleatoria permite un salto máximo de frecuencia de 10 MHz y que se
considera que se ha producido el salto cuando el error de frecuencia es inferior a 200 kHz. (Hacer los números para
ver si esto da resultados lógicos). (2.5p)
Para que se produzca el salto la variación en las condiciones que
marca el enunciado, y para el caso peor de salto de 10 MHz,
tenemos que:
∆f o (t ) 10 ± 0.2 0.98
=
=
1.02
∆f
10
En la gráfica el valor que limita es 1.02, y corta en abcisas en
ξωnTc =3.4. Para un tiempo de conmutación menor de 180 µsg,
despejamos y obtenemos que ωn ≥ 27 krad/sg
4.
Justifique que el valor de tiempo de asentamiento es compatible con la velocidad de salto definida en el “frequency
hopping” (1p)
La velocidad de salto definida en el “frequency hopping” es de 1600 saltos/sg, es decir que se produce un salto cada
1/1600=625µsg. Este valor es bastante superior a los 180µsg de tiempo de asentamiento del salto, con lo que no habría
problema de funcionamiento.
5.
El sistema permite aumentar la potencia transmitida hasta 20 dBm, insertando un amplificador de salida, para tener un
mayor alcance. Justifique qué Ganancia y P1dB del amplificador de salida se debería poner para poder obtener esta
potencia. ¿Qué tipo de amplificador pondría? ¿Qué rendimiento podría tener? (1.5p)
Para que funcione el sistema, necesitaríamos un amplificador de 20 dB de ganancia. El punto de compresión a 1 dB debería
ser mayor de 20 dBm para evitar la saturación. El amplificador puede ser no lineal por el tipo de modulación empleada (FSK)
y tendríamos un rendimiento del mismo de entre el 90 y el 99%
EJERCICIO 3. DISEÑO DEL RECEPTOR
1. Justifique, según los criterios vistos en clase, si la frecuencia intermedia seleccionada es adecuada. (2.5p)
a) La frecuencia intermedia no debe coincidir con la de señal
f i < f s (mínimo) ⇒ 110.6 MHz < 2402 Mz . Se cumple
b) La frecuencia intermedia no debe coincidir con el oscilador local.
f i < f OL (mínimo) ⇒ 110.6MHz < 1512.6 Mz . Se cumple
c)
La relación entre el valor de la frecuencia intermedia y el ancho de banda de la señal no debe ser muy grande.
f
110.6
2 < i < 100 ⇒ 2 <
< 100 . NO se cumple en sentido estricto, pero la banda del filtro es del 0.9%, realizable sin problemas.
Bi
1
d) Posibilitar el rechazo de las frecuencias interferentes.
fs
2480
< 50
⇒
= 22.42 < 50 Se cumple
110.6
fi
e) La frecuencia intermedia debe coincidir con uno de los valores normalizados.
No se cumple, pero no afecta porque es un demostrador de laboratorio. Se concluye por lo tanto que la elección es adecuada
2) Diga dónde se encuentra la banda imagen, y diseñe el filtro de RF de entrada para tener una atenuación de 40 dB en
dicha banda (frecuencia central, ancho de banda y número de etapas). El filtro es un Chebyshev de 0.5 dB de
rizado. Indique un esquema de cómo lo calcula. Si los filtros tienen una Q de 300, calcule las pérdidas del filtro
(2.5p)
La banda imagen se sítúa a +2fi de la señal correspondiente (OL superior).
Banda de señal: 2402-0.5 MHz a 2480+0.5 MHz (incluye el ancho de banda de la señal modulada)
2401.5 MHZ a 2480.5 MHz
Banda imagen: 2402+(2*110.6)-0.5 MHz a 2480+(2*110.6)+0.5 MHz
L(dB)
(incluye el ancho de banda de la señal modulada)
10
100
2622.7 MHz a 2701.7 MHz
5 4
90
El filtro de RF debe eliminar la banda imagen, dejando pasar la banda de
3
80
señal:
70
BRF=(2480.5-2401.5)79 MHz
60
f 0 = 2401.5 • 2480.5 = 2440.68MHz
79
w= BRF =
= 0.0324
f0
2440.68
50
fatenuar=2622.7 MHz
10
2
40
30
20
0
-1
n=1
-0.5
1 f
fo
w' =  atenuar −
w  fo
f atenuar

1  2622.7 2440.68 
 =
−

 = 4.45
 0.0324  2440.68 2622.7 
log(w'−1) = log(3.45) = 0.54
0
0.5
1
1.5
Log(ω’-1)
0.54
Por lo que n=3.
L0 (dB ) =
4.34 n
4.34
(1.5963 + 1.0967 + 1.5963) = 1.91
gi =
∑
wQ i =1
0.0324 • 300
3) Si el filtro anterior, a temperatura To, tiene unas pérdidas de 2 dB (independientemente del resultado del apartado
anterior), y el amplificador LNA una ganancia de 10 dB y figura de ruido de 3 dB y el mezclador una ganancia de
15 dB y una figura de ruido de 12 dB, calcule la relación mínima S/N de entrada al demodulador. Desprecie el efecto
de todos los elementos posteriores al mezclador, y considere una temperatura de antena de 300K. (To=290K y
k=1.38·10-23J/K) (2.5p)
Smin=-80 dBm
TRX = Ta + Tcadena = 300 + 1309.54 = 1609.54 K
Tcadena = T filtro +
TLNA
TMX
288.6 4306.19
+
= 169.61 +
+
= 1309.54 K
g filtro g filtro g LNA
0.631 0.631 • 10
T filtro = T0 (l − 1) = 290(10 0.2 − 1) = 169.61K
g filtro = 10 −0.2 = 0.631
TLNA = T0 ( f − 1) = 290(10 0.3 − 1) = 288.6 K
g LNA = 101 = 10
TMX = T0 ( f − 1) = 290(101.2 − 1) = 4306.19 K
N eq _ RX = KTRX BFI = 1.38 ⋅ 10 −20
mW
1609.54 K ⋅ 1MHz = 2.21 ⋅ 10 −11 mW = −106.53dBm
Hz ⋅ K
S
= −80 − (−106.53) = 26.53dB
 
 N  min_ DEM
4) Los dos filtros de frecuencia intermedia tienen unas pérdidas de 1.5 dB cada uno. El amplificador de frecuencia
intermedia tiene una ganancia de 20 dB y el circuito limitador de entrada al demodulador es en sí mismo un
amplificador de ganancia variable de 0 a 60 dB. Bajo estas premisas, y considerando el margen dinámico del
receptor, diga cuál es el margen dinámico de entrada al demodulador, especificando cuáles son las potencias
mínima y máxima de entrada al mismo. (2.5p)
Pmin_RX=-80 dBm y GMAX_FI=60 dB, por lo que :
Pmáx_RX= 0 dBm y GMIN_FI= 0 dB, por lo que:
Así:
MDDEM= Pmax_DEM- Pmin_DEM=40-20=20dB
Pmin_DEM=-80-2+10+15-1.5+20-1.5+60=20dBm
Pmax_DEM=0-2+10+15-1.5+20-1.5+0=40dBm