Relación3

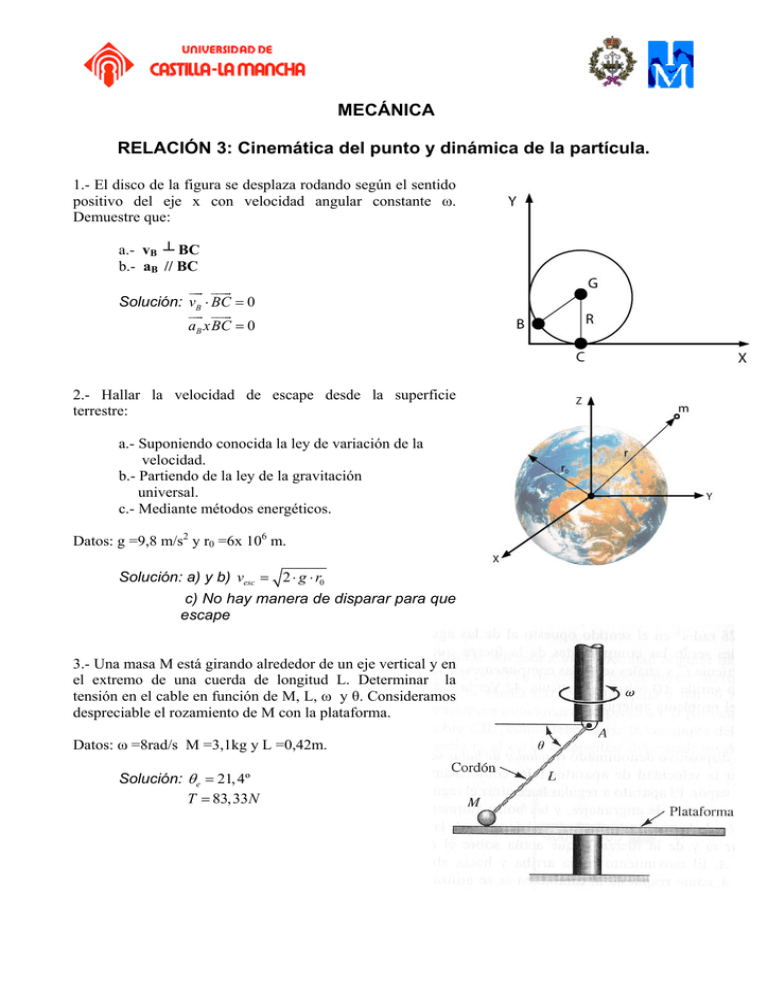
MECÁNICA
RELACIÓN 3: Cinemática del punto y dinámica de la partícula.
1.- El disco de la figura se desplaza rodando según el sentido
positivo del eje x con velocidad angular constante ω.
Demuestre que:
a.- vB ┴ BC
b.- aB // BC
JJG JJJG
Solución: vB ⋅ BC = 0
JJG JJJG
aB xBC = 0
2.- Hallar la velocidad de escape desde la superficie
terrestre:
a.- Suponiendo conocida la ley de variación de la
velocidad.
b.- Partiendo de la ley de la gravitación
universal.
c.- Mediante métodos energéticos.
Datos: g =9,8 m/s2 y r0 =6x 106 m.
Solución: a) y b) vesc = 2 ⋅ g ⋅ r0
c) No hay manera de disparar para que
escape
3.- Una masa M está girando alrededor de un eje vertical y en
el extremo de una cuerda de longitud L. Determinar la
tensión en el cable en función de M, L, ω y θ. Consideramos
despreciable el rozamiento de M con la plataforma.
Datos: ω =8rad/s M =3,1kg y L =0,42m.
Solución: θ e = 21, 4º
T = 83,33N
4.- Una partícula describe una trayectoria a helicoidal como
se muestra en la figura. Las ecuaciones paramétricas de la
trayectoria son:
⎧ R ⋅ sen (ωξ ) ⎫
G
⎪
⎪
r (ξ ) = ⎨ R ⋅ cos (ωξ ) ⎬
⎪c ⋅ ξ
⎪
⎩
⎭
Siendo ξ el parámetro que describe la trayectoria y R, c y ω
constantes. El módulo de la velocidad para ξ =0 es de V0 y el
ritmo de la variación de la velocidad es N.
Determinar la velocidad y la aceleración de la partícula para
ξ =0.
⎧1 ⎫
JJG
⎪ ⎪
Solución: v0 = v0 ⋅ ⎨0 ⎬ m s
⎪1 ⎪
⎩ ⎭
1
⎧
⎫
JJG ⎪ 2 ⎪
a0 = ⎨− 1 2 ⎬ m 2
⎪ 1 ⎪ s
⎩ 2 ⎭
5.- Obtenga la velocidad del extremo de la cuerda que se
desenrolla tensa de un cilindro a ritmo constante. Demostrar
que dicha velocidad es perpendicular a la cuerda.
⎧cos wt ⎫
G
⎪
2 ⎪
Solución: v(t ) = Rw t ⎨ senwt ⎬
⎪ 0 ⎪
⎩
⎭
G JJG
v ⋅ rPE = 0
6.- Determinar la velocidad con la que debe lanzar la bola
para que alcance la posición B.
a.- Suponiendo que AO es una barra rígida
articulada en O.
b.- Suponiendo que AO es una cuerda.
Solución: v0 > 2 gL
v0 ≥ 3 gL
7.- Calcular el radio de la órbita geoestacionaria, conocidos
su g = 9,81m/s2 y ro =6378Km.
Solución: r = 42257 km
8.- Determine la velocidad límite de una persona que se cae
con un paracaídas de 10m de radio. ¿Y sin paracaídas?.
Suponer que el comportamiento aerodinámico de un hombre
en caída vertical puede asimilarse al de una placa de
dimensiones 0,5m x 2m.
Datos: Coeficiente aerodinámico de un paracaídas: Cx =1,2.
Coeficiente aerodinámico de una placa: Cx =1.
Solución: Con paracaídas v = 6,9km / h
Sin paracaídas v = 133, 4km / h
9.- Calcula la aceleración del vehículo de prácticas.
Solución: Como sólido libre a =
1
(F − T )
m
⎛ R ⋅R
⎞ T
Aislando sistema de tracción a = ⎜ 1 P − 1⎟ ⋅
⎝ R2 ⋅ Rr
⎠ m
⎛ 2 ⋅ RP ⎞ T
Con R1 = 2 R2 a = ⎜
− 1⎟ ⋅
R
⎝ r
⎠ m
G
Si Rr > R p ⇒ a = 0
Casos:
1
Rr ⇒ a < 0
2
1
R p = Rr ⇒ a = 0
2
1
R p > Rr ⇒ a > 0
2
Rp <