Curso 09/10 (Convocatoria Julio)
Anuncio

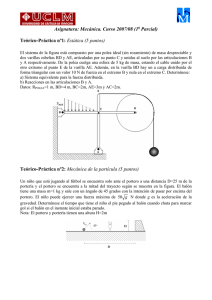
Mecánica. Curso 2009/10 (Final Julio) Bloque I Teórico-Práctica nº1: Estática (5 puntos) Se tiene un pórtico compuesto por una varilla de longitud L y masa m, empotrada en el suelo, una placa en forma de triángulo rectángulo isósceles de lado L y masa m y una viga AB lisa de masa 2m y longitud 2L. La viga AB se apoya sobre la viga de la izquierda (pto A) y está articulada en la placa derecha (pto B), tal y como se muestra en la figura. En la viga AB se aplican 2 fuerzas, una formando un ángulo de 45 grados en el punto A de módulo 4F y otra distribuida con dirección vertical desde el centro de masas de la viga con valor nulo aumentado linealmente hasta el punto B donde toma su valor máximo de módulo FMAX=F. Si la placa de la derecha está a punto de volcar sin deslizar, determínese: (a) Sistema equivalente de la fuerza distribuida en el centro de masas de la varilla. (b) Módulo de la fuerza F para que se produzca el vuelco. (c) Coeficiente de rozamiento mínimo compatible con el equilibrio para que la placa no deslice antes del vuelco. (d) Razonar si la varilla empotrada debe soportar algún momento en el empotramiento. Datos=M=100 kg y L=1m F FMAX A B L Teórico-Práctica nº2: Mecánica de la partícula (5 puntos) En un experimento se estudia una partícula y se determinan los siguientes datos de su movimiento G G G G (1) La proyección de la aceleración a en dirección del vector b = i + j es igual a 2 . G G G (2) El producto vectorial del vector b anterior por la aceleración b × a es igual al vector G G G G c = 2ti − 2tj + 2k . (3) En el instante t=1s está en la posición (3;1;-2/3). (4) En el instante inicial la velocidad tiene un módulo igual a 2 y perpendicular al plano YZ. Determínese: (a) Velocidad y aceleración de la partícula. (b) Ecuaciones horarias y trayectoria de la partícula. (c) Aceleración tangencial y normal de la partícula. (d) Espacio recorrido entre el instante inicial y posición (3;1;-2/3). Mecánica. Curso 2009/10 (Final Julio) Problema nº1: Movimiento Relativo (10 puntos) Se considera el mecanismo plano de la figura constituido por las varillas AB y CD, y una placa cuadrada de centro P. La varilla AB tiene una longitud 2L, la varilla DC 2L y lado BC de la placa tienen una longitud L. Las varillas AB y CD rotan alrededor de los puntos fijos A y D, respectivamente. La placa está articulada a las varillas AB y CD por sus extremos según se muestra en la figura. Se sabe que la velocidad angular de la varilla AB es constante igual a ωAB=ω con sentido antihorario. Determínese en el instante de la figura: (a) Velocidades angulares de la placa ωP y varilla CD ωCD. (b) Aceleración angular αP de la placa y αDC varilla DC. (c) Velocidad y aceleración absoluta del punto P de la placa. (d) Aceleración de coriolis del punto P para observador en varilla AB ubicado en el pto B. Datos: L=2 m Bloque II Teórico-Práctica nº1: Cinemática del Sólido Rígido (5 puntos) Se tiene un disco de radio R=2m que se lanza deslizando hacia abajo sin rodar sobre un plano inclinado 30 grados con la horizontal con una velocidad inicial V0. Inmediatamente empieza a rodar y deslizar por acción de la fuerza de rozamiento hasta que alcanza la rodadura pura. Se sabe que los g módulos de la aceleración del centro de masas y la aceleración angular son AG = 1 − 3μ y 2 3μ g α= , respectivamente Determínese: R a) La posición de los sucesivos centros instantáneos de rotación respecto al centro de masas hasta que alcanza una rodadura pura. b) Condición que se debe dar para rodadura pura en la ecuación determinada en el apartado anterior y tiempo para la rodadura pura. c) Razonar el que valor mínimo debe tener el coeficiente de rozamiento para alcanzar la rodadura pura. ( ) Mecánica. Curso 2009/10 (Final Julio) Teórico-Práctica nº2: Sistema de partículas (5 puntos) Se tiene un sistema compuesto por dos masas puntuales unidas a una varilla ABC de masa despreciable con forma de escuadra de longitud 2L (AB=BC=L). En la posición C está unida la partícula de masa m y en el punto B la 2m. En la posición inicial el sistema está en reposo con el punto C de la escuadra en la vertical con la articulación (posición A), según se muestra en la figura. Si en este instante se libera el sistema obténgase la velocidad angular de la varilla cuando la varilla AB ha girado un ángulo de 135º. Problema nº1: Mecánica del Sólido Rígido (10 puntos) Se tiene una polea de radio R compuesta por un disco de radio R y masa 5m solidariamente unida a la mitad de un eje de longitud L y masa 2m. El eje está apoyado en 2 soportes A y B con unos rodamientos que no ofrecen resistencia al giro. El sistema está accionado por un motor de potencia P y par T para hacer girar el sistema. La máquina se emplea para subir una masa 50m. El cable que une la polea con la masa es ideal y con masa despreciable. La masa puntual asciende desde una posición en reposo en 10 s una altura de 100m con aceleración constante. Determinar: (a) Tensión en el cable. (b) Tensor de inercia del sistema polea y eje en el centro de masas. (c) Par y potencia del motor para que pueda subir la masa puntual (analizar todo el trayecto). (d) Reacciones en los soportes A y B de la máquina. Datos: m=10 kg y L=R=1/2m. La polea puede ser considerada un disco de espesor despreciable y el eje una varilla. B A A m m