Diagramas de fase con punto eutéctico

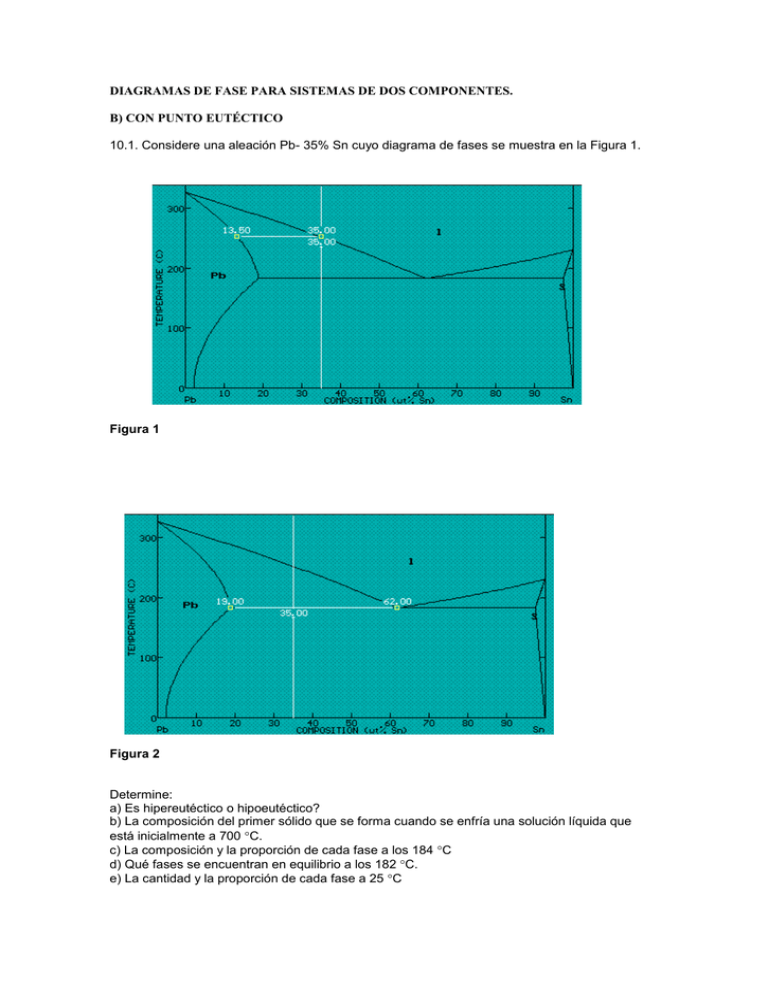
DIAGRAMAS DE FASE PARA SISTEMAS DE DOS COMPONENTES.
B) CON PUNTO EUTÉCTICO
10.1. Considere una aleación Pb- 35% Sn cuyo diagrama de fases se muestra en la Figura 1.
Figura 1
Figura 2
Determine:
a) Es hipereutéctico o hipoeutéctico?
b) La composición del primer sólido que se forma cuando se enfría una solución líquida que
está inicialmente a 700 C.
c) La composición y la proporción de cada fase a los 184 C
d) Qué fases se encuentran en equilibrio a los 182 C.
e) La cantidad y la proporción de cada fase a 25 C
Resolución:
A fin de responder a esas preguntas dibujaremos distintas líneas en el diagrama de fases.
a) Como la aleación tiene una composición global de 35 % de Sn, la cual es menor que la
composición eutéctica de 62 %, se dice que la aleación es hipoeutéctica.
b) El primer sólido que se forma durante la solidificación lo hace cuando la muestra se enfría y
llega a la línea de “líquidus”. La fase sólida que está en equilibrio con la solución líquida
tiene 13.5 % de Sn, como lo indica la Figura 1. Esta es por lo tanto la composición de la
primera porción de fase sólida formada.
c) Inmediatamente antes de la transformación eutéctica la muestra consiste de líquido y sólido
. La fase sólida a esa temperatura contiene 19% de Sn y la concentración del líquido es 62%
de Sn.
En la Figura 2 se muestra la línea horizontal que corresponde a 184 C.
Para calcular la relación que existe entre la fase sólida y la fase líquida podemos aplicar la regla
de la palanca:
% masa sólida= (CL-CO)/ (CL-CO)= (62 - 35)/(62-19)=62.79 %.
% masa líquida= 1-masa sólida= 37.21 %
La muestra contiene entonces 62.79 % de fase alfa y 37.2% de fase líquida.
d) A la temperatura de 182 C estamos justamente por debajo de la temperatura eutéctica.
Consecuentemente, la muestra ha solidificado y consiste en dos fases (fase , rica en plomo
[19% Sn, 81 % Pb] y fase  rica en estaño [97,5 % Sn, 2,5 % Pb])
Figura 3
e) Cuando identificamos las fases en equilibrio a 25 C ( Figura 4) observamos que ellas son
una fase rica en Pb ( [alfa]) y otra rica en Sn (  [beta]), sin embargo, comparando con las
fases en equilibrio a 182 C la composición de las mismas ha cambiado. Ha disminuido la
solubilidad de cada elemento, así, la fase rica en Pb contiene sólo 2.75 % de Sn, mientras que
la fase rica en Sn contiene sólo 0.25 % de Pb. La proporción (cantidad relativa) de la fase alfa
en la mezcla alfa + beta será:
Figura 4
(cantidad relativa de alfa en la mezcla) = (CSn  - CSn o)/( C Sn  - CSn )=
Como CSn = 99,75%, CSn =2,75%
= 66,75% el resto (33,25 %) será de fase .
Problema 10.2
Una aleación contiene 45 % de fase alfa y 55% de fase beta a 100 oC. Determine la
composición de la aleación. Es hiper o hipo eutéctica?
Figura 5
Trazando la línea horizontal a 100 oC encontramos que la composición de las fases alfa y beta
son:
CSn = 7,5 % y
CSn= 98,5 %
= (CSn – Co)/ (CSn -CSn)
C0= CSn - ( CSn -CSn)= 57,55%
Por lo tanto la concentración global de la aleación es de 57,55%.
Problema 10.3
Una aleación contiene 23 % de la fase alfa (rica en plomo) y 77% de una microestructura de
composición eutéctica. Determine la composición de la aleación. Como la composición de una
de las fases es la eutéctica significa que la temperatura es similar a la temperatura eutéctica.
Figura 6
Sabemos el % de cada fase por el gráfico
Ceut= 62%, C=19%
Podemos calcular la composición global Co como:
= (Ceut - Co)/( Ceut - C)
de donde Co=52,11% (es decir la aleación contiene 52,11 % de Sn).
Como este valor es menor que el 62 % correspondiente a la composición eutéctica, entonces
se dice que es hipoeutéctica.
Problema 10.4.
Se realiza un enfriamiento lento de una aleación Pb-Sn desde 230 C de acuerdo a la Figura 7.
Observar los cambios de composición de las fases y de la cantidad relativa de cada fase en el
sistema (fase  + solución líquida L) de acuerdo a la figura 7.
Tabla I
Ti(oC)
230
225
215
205
195
C(Sn)%
15
16
17
18.25
18.75
C(Pb)%
85
84
83
81.75
81.25
CL (Sn)%
40.75
45
49.5
55
25
CL(Pb)%
59.25
55
50.50
44.75
39.5
Podemos calcular la proporción de la fase alfa a 215 oC como:
215=(CL215- Co)/( CL215-C215)= 29,23%
De la misma forma se puede calcular la proporción a otras temperaturas y obtenemos:
Ti(oC)
230
225
215
205
195
%215Sn
2.91
17.24
29.23
41.22
49.1
%L215Sn
97.09
82.76
70.77
58.78
50.9
Tal cual se muestra en el dibujo lateral del diagrama la proporción de fase sólida aumenta al
disminuir la temperatura desde 2 % hasta casi la mitad a temperaturas próximas a la eutéctica.
Al aumentar la proporción de fase sólida (roja) rica en Pb disminuye la proporción de Pb en la
fase líquida (negra) para mantener en todo momento el balace de masa.
Figura 7
Problema 10.5
Una muestra que contiene 40% de estaño 60% de Pb ha sido enfriada lentamente desde la
temperatura eutéctica hasta 0o C. Cuál es la composición de las fases presentes a las
temperaturas de 180, 135, 90, 50 y 10 o C .
Del gráfico podemos obtener la siguiente información.
Tabla 1
Ti
180
135
90
50
10
Sn(%)
18,75
12,00
6,5
3,5
2,25
fase rica en Pb
Pb(%)
81,25
88,00
93,5
96,5
97,75
Sn(%)
97,5
98
98,75
99,25
100
fase rica en Sn
Pb(%)
2,5
2
1,25
0,75
0
Usando la regla de la palanca podremos llegar la discribir la composición de las fases en
equilibrio a cada temperatura.
A la temperatura eutéctica (182 oC) podemos observar en la figura que la composición de las
fases en equilibrio es de
Co= 40%, CL= 62 %, C=19%
Para calcular la cantidad de masa líquida en equilibrio con las dos fases sólidas  y  a la
temperatura eutéctica planteamos:
masa Líquida (%)= (C0 - C)/(CL- C)= 48,84 %
para calcular la masa  en equilibrio
= ( Co - Sn )/ (Sn - Sn)
= 1- 
La Tabla 2 siguiente muestra el % de cada fase de acuerdo a la temperatura.
Tabla 2
T /o C
180
135
90
50
10
%
26,98
32,56
36,31
38,12
38,62
%
73,02
67,44
63,69
61,88
61,38
La muestra es sólida en todos los casos pero la microestructura está constituida por dos fases
 y . La composición de dichas fases así como la cantidad relativa de las mismas varían con
la temperatura como muestran las Tablas 1 y 2.