Equilibrio sólido-‐líquido en sistemas de dos componentes
Anuncio

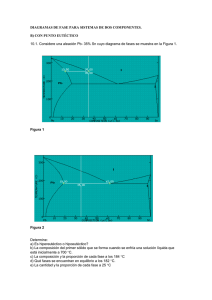
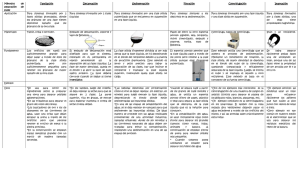
Equilibrio sólido-­‐líquido en sistemas de dos componentes Miscibilidad en fase líquida e inmiscibilidad en fase sólida: sean C y B dos sustancias miscibles en todas las proporciones en la fase líquida y completamente inmiscibles en la fase sólida. Donde TB* y TC* son los puntos (temperaturas) de congelación de B puro y C puro. E es el punto eutéctico que es el punto de temperatura más baja a la cual puede fundir una mezcla de B y C con una composición fija. El gráfico representa un diagrama de fases de sistemas eutécticos simples (Pb-Sb, benceno-naftaleno, Si-Al, KCl-AgCl, Bi-Cd, etc) Por lo tanto la ecuación para la curva DE es: R ln xB ≈ ΔfusHm,B [ (1/TB*) – (1/T)] Donde para la curva AE se emplea la misma ecuación solo que introduciendo los siguientes cambios: R ln xC ≈ ΔfusHm,C [ (1/TC*) – (1/T)] Así la regla de la palanca para el segmento GHI quedaría: nCs HI = (nBl + nCl) HG Donde nCs es el número de moles de C sólido en el equilibrio con una disolución de nBl moles de B nCl moles de C. En el punto f, la regla de la palanca nCs = 0. A medida que T desciende a lo largo de FHK la distancia horizontal a la línea AFGE aumentam indicando un aumento de nCs. Si T disminuye se alcanza el punto K que es de alguna manera la temperatura eutéctica. En este punto la disolución tiene una concentración xB’’’ (punto E) y tanto el sólido C y el sólido B se congelan. Esto es porque la disolución de composición eutéctica se enfría. Disoluciones sólidas Ciertos pares de sustancias forman disoluciones sólidas. En una disolución sólida de B y C no existen cristales individuales de B o de C. Por el contrario, las moléculas, átomos o iones se mezclan unos con otros a nivel molecular, y la composición de la disolución se puede modificar de forma continua a lo largo de un cierto intervalo. Ejemplos: Acero, Cu-Ni, Na2CO3-K2CO3 y p-diclorobenceno-p-dibromobenceno. El ZnO suele tener una relación molar Zn/O ligeramente mayor que 1. La explicación es que es una disolución sólida intersticial de Zn en ZnO. Por lo tanto no viola la Ley de proporciones definidas. Miscibilidad en fase líquida y en fase sólida: ejemplo el diagrama de fases sólido-líquido del sistema Cu-Ni a 1 atmósfera. Cu-Ni, Sb-Bi, Pd-Ni, KNO3-NaNO3 y d-carvoxima-l-carvoxima son ejemplo de sustancias completamente miscibles en fase solida. Miscibilidad en fase líquida y miscibilidad parcial en fase sólida Diagrama Eutéctico Solubilidad total en estado líquido y nula en sólido Eutéctico: punto invariante (F= 0) en el que un líquido (L) se transforma en otros dos sólidos diferentes (α y β). L + α L + β Reacción eutéctica L → α + β L α + β Diagrama con punto de equilibrio Peritéctico Punto invariante (F = 0) en el que un líquido (L) y una fase sólida (ε) se transforman en otra sólida distinta (η). Reacción peritéctica: L+ ε→η Diagramas con punto de equilibrio PERITECTOIDE Peritectoide: punto invariante (F = 0) en el que dos sólidos (α y β) se transforman en otro sólido diferente (γ). Reacción peritectoide • α+β→ γ Diagramas de equilibrio con EUTECTOIDE Eutectoide: punto invariante (F= 0) en el que un sólido (γ) se transforma en otros dos sólidos diferentes (α y β). Reacción eutectoide γ → α + β Aquí un calentamiento adicional posterior a la transición del punto H nos lleva en primer lugar a la región bifásica β y la disolución líquida y finalmente a la región de una sola fase de disolución líquida. Una transición peritéctica (transición en el punto H) es aquella en la que el calentamiento transforma una fase sólida en una fase líquida mas una segunda fase sólida: s1 à liq + s2 Nota: en la transición eutéctica, el calentamiento sigue el esquema s1 + s2 = líq. FORMACIÓN DE COMPUESTOS: Miscibilidad en fase líquida e inmiscibilidad en fase sólida. El compuesto funde congruentemente. T FORMACIÓN DE COMPUESTOS: Formación de compuestos con fusión incongruente, miscibilidad en fase líquida e inmiscibilidad en fase sólida. El punto P se denomina PUNTO PERITÉCTICO, Cuando se forman compuestos, existe la posibilidad de que aparezca más de un punto peritéctico. Métodos Experimentales: Análisis Térmico T es directamente proporcional a cantidad de calor que pierde el sistema, por lo que la pendiente dT/dt de una curva de enfriamiento es aproximadamente proporcional a la inversa de la capacidad cal’orica del sistema: Cp = dqp/dT Solubilidad Solubilidad… Para la mezcla eutéctica NaCl-H2O la temperatura eutéctica es de -21 ° C y para el sistema CaCl2 6H2O – H2O es de -50 °C. Calculo de diagrama de fases por ordenador Sistema ternario Para representación bidimensional, las concentraciones de los tres componentes a P y T dadas, se grafican sobre un triangulo equilátero: • Cada vértice del triangulo representa el 100% del componente con que se designa. • Las divisiones o líneas paralelas al lado BC, dan los porcentajes de A, que van desde 0%A (sobre BC) hasta 100%A (vértice). • Análogamente, las líneas que dividen los lados BA y BC y son paralelas a AC nos dan los porcentajes de B, y las que dividen a CA y CB y paralelas a AB representan los porcentajes de C. • Para graficar un punto sobre el diagrama tal como D, localizamos su composiciones en 30% de A, 20% de B y por ende 50% de C, el cual queda definido. Sistema TiO2-­‐FeO-­‐Fe2O3 a altas temperaturas L. A. Bursill, J. Solid State Chem. 1974, 10, 72. En resumen… Sistemas de tres componentes (ternario) Para un sistema ternario: f = 3 – p + 2 = 5-p La regla de la palanca en sistemas ternarios: nα = (xB – xBα ) = nβ (xBβ - xB) K = punto de pliegue o punto crítico isotérmico. Donde: nα y nβ son el número total de moles de todas las especies en las fases α y β. También xB, xBα , xBβ son la fracción molar global de B, la fracciópn molar de B en la fase α y fracción molar de B en la fase β. Recurriendo a la trigonometría se puede demostrar que: lα nα = lβ nβ …1 Donde : lα y lβ son las longitudes de las líneas de conjunción que dan las composiciones de las fases α y β. En el ejemplo: FG nF = GH nH. Siendo nF y nH el número de moles totales en las fases cuya composición viene dada por los puntos F y H.