taller no 3 cálculo diferencial 2016-1
Anuncio

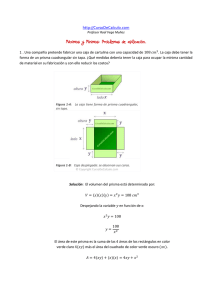
UNIVERSIDAD DEL MAGDALENA ÁREA DE MATEMÁTICAS Asignatura: Cálculo Diferencial TALLER No. 3 2016-1 Dependencia: Facultad de Ciencias Empresariales y Económicas I. Determine los valores críticos si los hay, intervalos crecientes o decrecientes y los extremos relativos (máximos y mínimos locales) de cada función usando el criterio de la primera derivada. 1. 𝑞 (𝑥 ) = 𝑥 5 − 5𝑥 4 + 5𝑥 3 − 10 2 2. ℎ(𝑥 ) = 𝑥𝑒 −𝑥 3. 𝑖 (𝑥 ) = 𝑥 3 + 1 II. Encuentra los valores de 𝑥 para los cuales las siguientes funciones son: cóncavas hacia arriba o cóncavas hacia abajo. También determine los puntos de inflexión y los valores máximos y mínimos absolutos utilizando el criterio de la segunda derivada, si existen. Bosqueje la gráfica. 1. 𝑓 (𝑥 ) = 5𝑥 4 − 15𝑥 + 2 1 1 2. 𝑗(𝑥 ) = 𝑥 3 − 𝑥 2 − 2𝑥 3 2 3. 𝑔(𝑥 ) = 𝑥 5 − 5𝑥 3 III. Resuelva los siguientes problemas de aplicación de máximos y mínimos relativos. 1. Una compañía ha encontrado que las funciones de ingreso 𝐼 (𝑥 ) y de costo C(𝑥 ) para un ventilador de pedestal domestico son: I (𝑥 ) = 250𝑥 − 0,5𝑥 2 y C(𝑥 ) = 1200 + 125𝑥 − 0,05𝑥 2 . Calcula la cantidad 𝑥 de ventiladores que deben producir para obtener la máxima utilidad. 2. Un fabricante de altavoces para computadora ha encontrado que el precio 𝑝 y el número 𝑥 de altavoces del modelo SR – 71 que logra vender a ese precio están 𝑥 relacionados por la expresión 𝑝(𝑥 ) = 500 − 2 . Por otra parte, saben que el costo C de producir 𝑥 de esos altavoces viene dado por C(𝑥 ) = 12000 + 125𝑥 − 0,001𝑥 2 . a. Determina 𝑥 como una función de 𝑝 . b. Expresa 𝐶(𝑥) como una función de 𝑝. c. Calcula el valor de 𝑝 que minimiza el costo de producción. 3. El costo de uninventario 𝑥 en una cadena de comidas está dado por: I(𝑥 ) = 0,5𝑥 ¿Cuál debe ser su inventario mensual para minimizar el costo? 25000 𝑥 + 4. Para construir un edificio de oficinas, los costos fijos son de $2, 5 millones e incluyen el precio del terreno, los honorarios del arquitecto, la cimentación, la estructura, etc. Si se construyen 𝑥 pisos, el costo (excluyendo los costos fijos) es 𝐶 (𝑥 ) = 5𝑥 [100.000 + 5000(𝑥 − 1)]. El ingreso por mes es de $50.000 por piso. ¿Cuantos pisos darán una tasa máxima de rendimiento sobre la inversion? (Tasa 𝐼𝑛𝑔𝑟𝑒𝑠𝑜 𝑇𝑜𝑡𝑎𝑙 de rendimiento = 𝐶𝑜𝑠𝑡𝑜 𝑡𝑜𝑡𝑎𝑙 ) IV. Encuentra la derivada parcial de la función con respecto a cada una de las variables indicadas. 1. 𝑓 (𝑥, 𝑦) = 𝑥 3 𝑦 2 + 2𝑥 2 𝑦 − 4𝑥𝑦 + 3𝑦 2. 𝑓 (𝑥, 𝑦) = 𝑥 2 + 3𝑥𝑦 + 𝑦 2 √𝑥 2 + 𝑦 2 V. En los siguientes ejercicios, evalúe las derivadas parciales en el punto dado: 1. 𝑔(𝑥, 𝑦, 𝑧) = 𝑒 𝑥 √𝑦 + 2𝑧, 2. 𝑓 (𝑥, 𝑦) = 𝑥 3 𝑦 + 7𝑥 2 𝑦 2 , 𝜕𝑔 𝑒𝑛 (0, 6, 4) 𝜕𝑧 𝜕𝑓 𝑒𝑛 (1, −2) 𝜕𝑥 VI. Resuelva los siguientes problemas de aplicación de las derivadas parciales 1. Supongamos que la función de producción de Cobb-douglas para una compañía está dada por 𝑧 = 100𝑥 1/4 𝑦 3/4 , donde x es la inversión de capital de la compañía (en dólares) e y es el tamaño de la fuerza laboral (en horas de trabajo). a. Encuentre la productividad marginal del capital b. Si la fuerza laboral actual es de 625 horas de trabajo, sustituya y 625 en su respuesta para el inicio (a) y trace el resultado. c. A partir de la gráfica en (b) ¿qué se puede decir acerca del efecto que tendría sobre la producción una inversión de capital adicional si las horas de trabajo se mantienen en 625? 2. 𝜕𝑞 𝜕𝑞 Dos productos A y B son complementarios si 𝜕𝑃𝐴 < 0 y 𝜕𝑃𝐵 < 0 , son competitivos 𝐵 o sustitutos si 𝜕𝑞𝐴 𝜕𝑃𝐵 >0 y 𝜕𝑞𝐵 𝜕𝑃𝐴 𝐴 > 0 de lo contrario no son ni sustitutos ni complementarios. Las funciones de demanda para los productos A y B son cada una función de los 50 3 pB 75 p A precios de A y B y están dadas por q A y qB respectivamente. 3 pA pB2 Determinar si A y B son productos competitivos o complementarios, o ni lo uno ni lo otro, para 𝑝𝐴 = 4 y 𝑝𝐵 = 2. Rúbrica de Evaluación de Trabajo Extra-clase Ítem Evaluado Contenido 60% Presentación 40% Puntualidad Insuficiente Aceptable Sobresaliente Excelente No El trabajo no da El trabajo El trabajo muestra El trabajo presentó el respuestas muestra algunas la solución muestra la trabajo adecuadas a la respuestas adecuada de la solución eficiente solución de los adecuadas a la mayor parte de los de todos los problemas solución de los problemas problemas planteados en problemas planteados en la planteados en la la actividad planteados en la actividad actividad actividad 0 3 6 9 12 El trabajo no tiene la La presentación Se evidencia el Excelente mínima norma de del trabajo es interés de entregar presentación presentación aceptable un trabajo bien presentado 0 4 6 8 Solo se reciben trabajos en la fecha indicada