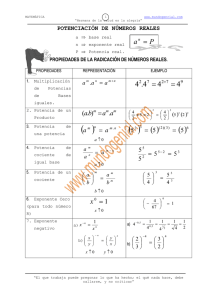
RADICACIÓN DE NÚMEROS REALES
Anuncio

MATEMÁTICA
1
“Hermana de la salud es la alegría”
n
b = r
JRC
rn = b
⇔
” el símbolo, “b” el radicando o cantidad subradical y “r” la raíz.
Donde: “n” es el índice, “
PROPIEDADES DE LA RADICACIÓN DE NÚMEROS REALES.
REPRESENTACIÓN
una raíz
)
n
a
Raíz de un cociente
n
a
=
b
n
n
Raíz de otra raíz.
Raíz de un producto
DO
a
Si
el
=
.M
UN
racional
m
n
radicando
es
a =b
el
radicando
es
a
m
W
el
radicando
= 8
3
−8 −2
=
3
27
8
5
4
0,25 = 0,5
4
2
= 22 = 4
1
=
64
6
6
6
1
1
=
2
64
4•
1
1 2
= 2• =
9
3 3
=
4
85
por que:
(0,5)2 = 0,25
−1
1
≠− ,
16
4
2
porque
es
positivo negativo y el
índice impar
1
=
9
(b)2 = a
W
W
Si
4•
−a
c
≠− ,
b
d
negativo y el índice es
par
a
por que:
positivo y el índice par
Si
n
3
=2
4
1
=
64
3
a.b = n a .n b
n
Potencia de exponente
a =
m.n
−8
=
27
2
GE
m n
3
m
n
bm = b
2
2
a
b
Raíz de una potencia
n
( 8)
= a
OM
n
L.
C
(
Potenciación enésima de
EJEMPLO
NI
A
PROPIEDADES
3
a
=
b
3
3
a
c
= +
d
b
1
1
− =
16
4
3
27
3
=
64
2
3
− 27
−3
porque:
=
64
4
3
− 27
− 3
=
64
4
“El que trabaja puede pregonar lo que ha hecho; el qué nada
hace, debe callarse, y no criticar”
MATEMÁTICA
2
“Hermana de la salud es la alegría”
JRC
EJERCICIOS
(
)
(
)
(
)
La raíz quinta de menos 1 es – 1
(
)
5.
La raíz cúbica de – 27 es – 3
(
)
6.
En
(
)
7.
Si se tiene 100
OM
Colocar verdadero (V) p falso (F) después de analizar cuidadosamente los siguientes enunciados
(
)
8.
Poniéndose
(
)
(
)
(
)
(
)
(
)
x = y , entonces “x” es el índice “y” el radicando y “m” la raíz
1.
Si tiene
2.
La raíz cuadrada de menos 64 pertenece a los números R
3.
Si n = 2, b = 0 ⇒
4.
0 , porque (0 ) = 0
2
1
= a
1
2
0 =0
⇒ el radicando es igual a la raíz
1
m .n
9.
n
a
10.
n
am + a = a
m
= −10 , es una afirmación verdadera
( m +1)
n
GE
11.
12.
Simplificar: E =
1
2
c) 5
d) 5 0
3
W
e) 5 8
Aplica propiedades para resolver los siguientes propiedades:
W
2.
.M
UN
1
a) 5 8
b) 5
125
(aplicar propiedades)
DO
RESUELVE LOS SIGUIENTES EJERCICIOS:
1.
L.
C
64 = 2 , se lee “ La raíz sexta de 64 es 2”
NI
A
6
m
W
54 =
4 1
x
=
9 25
3
−8
=
1000
4
1
=
16
3
− 0,027 =
1
=
64
16
=
64
7
1=
9
=
49
“El que trabaja puede pregonar lo que ha hecho; el qué nada
hace, debe callarse, y no criticar”
MATEMÁTICA
− 27
=
8
4
81 =
100 =
− 32 =
1
=
49
256 =
3−2 =
3 24 =
1
=
49
Rpta.-
55
7
GE
16 −
2x
1
=
2
Rpta.- 1
1
2
DO
5.
1
=
8
.M
UN
2. 2 − 3
Rpta.- 1
W
6.
W
W
4.
NI
A
L.
C
N = 169 − 25 −
− 64 =
N = 169
256 =
25 =
3.
3
JRC
OM
3
3
“Hermana de la salud es la alegría”
7.
256 − 32 =
Rpta.- –1
( 8 x 8 )( 6 2 x 32 ) =
“El que trabaja puede pregonar lo que ha hecho; el qué nada
hace, debe callarse, y no criticar”
MATEMÁTICA
JRC
1 3
=
2 27
4 x64 −
8.
( 1)
L.
C
−1
=
81
2
÷
−1
144
18
.M
UN
11. Si: Q =
− 3
−2
NI
A
3
24
GE
10.
OM
9
16
+
=
4
4
3
DO
9.
4
“Hermana de la salud es la alegría”
Hallar Q −2 =
1
49
W
W
12. Si: N = 169 − 25 −
W
Hallar:
13. P =
N
=
2
1
−
256
1
“El que trabaja puede pregonar lo que ha hecho; el qué nada
hace, debe callarse, y no criticar”
MATEMÁTICA
Hallar:
5
“Hermana de la salud es la alegría”
JRC
P −3 =
RACIONALIZACIÓN DE DENOMINADORES.- Cuando una fracción de denominador irracional se
transforma en otra fracción equivalente con el denominador racional, se conoce con el nombre de
racionalización de denominadores.
A) CUANDO EL DENOMINADOR ES UN MONOMIO.- Se busca un radical apropiado que multiplicado
por el radical dado, dé una fracción con denominador racional. Este último radical se multiplica
SOLUCIÓN:
1
5
Se tiene:
Entonces:
1x 5
5
1
=
=
=
5
5x 5
5 x5
1
=
5
5
Rpta.
5
5
5
=
5
25
L.
C
Racionalizar:
NI
A
EJEMPLO:
OM
también en el numerador.
1
7
2)
Racionalizar
6
6
3)
Racionalizar
DO
Racionalizar
2
3
W
W
W
.M
UN
1)
GE
EJERCICIOS
4)
Racionalizar:
4
8 3
“El que trabaja puede pregonar lo que ha hecho; el qué nada
hace, debe callarse, y no criticar”
MATEMÁTICA
5)
6
“Hermana de la salud es la alegría”
Racionalizar:
JRC
−5
5
B) CUANDO EL DENOMINADOR ES UN BINOMIO.- El binomio denominador se multiplica por su
SOLUCIÓN:
3
2+ 3
3
3( 2 − 3)
=
=
2 + 3 ( 2 + 3 )( 2 − 3 )
=
6 − 32
6 −3
=
= −( 6 − 3)
−1
2−3
3
= − ( 6 − 3) Rpta.
2+ 3
GE
Entonces:
3( 2 ) − 3( 3 )
=
( 2 ) 2 − ( 3) 2
NI
A
Ejemplo: Racionalizar
L.
C
(de 3 + 5 su conjugada es: 3 − 5 )
altere. Así:
OM
conjugada. Este último binomio también se multiplica en el numerador para que la fracción no se
Racionalizar:
2)
Racionalizar:
3
=
3− 5
1
=
2− 3
W
W
W
.M
UN
1)
DO
EJERCICIOS:
3)
Racionalizar:
5 2
=
4+ 3
“El que trabaja puede pregonar lo que ha hecho; el qué nada
hace, debe callarse, y no criticar”
MATEMÁTICA
7
“Hermana de la salud es la alegría”
Racionalizar:
2+ 3
=
2− 3
5)
Racionalizar:
−3
=
x −2
W
W
W
.M
UN
DO
GE
NI
A
L.
C
OM
4)
JRC
“El que trabaja puede pregonar lo que ha hecho; el qué nada
hace, debe callarse, y no criticar”
MATEMÁTICA
8
“Hermana de la salud es la alegría”
JRC
VALOR ABSOLUTO DE NÚMEROS REALES.- Para cualquier número real x, su valor absoluto se
simboliza por x y se define así:
x =
{
X
si x > 0 (x positivo)
0
si x = 0
–x
si x < 0 ( x negativo)
OM
EJEMPLOS:
1
1
1 − 26 − 25
1
2) −
− + 6,5 = − 6,5 = − 6,5 =
=
2
4
4
4
2
2
1) − 4 = −( −4) = +4
2
L.
C
Se observa de los ejemplos expuestos que para todo número real x, su valor absoluto x siempre es
positivo: − x = x
1)
NI
A
EJERCICIOS
Hallar el valor absoluto de:
2
− 3
a)
=
3
=
3
=
c)
3
.M
UN
3
3
2)
GE
−2
DO
−3
b)
9
2
3
d) − =
2
e) − 2,5 =
f) − 5
−2
=
EFECTUAR
3
−4
+1 ÷ − 4 =
5
2
W
W
a)
b) 4 − − 5 − 4,5 =
2
2
W
2
c)
2 − 12 1 − 1
x
+ •
=
6
5
2
2
2
3
d) + 1 • − 1,6 =
2
“El que trabaja puede pregonar lo que ha hecho; el qué nada
hace, debe callarse, y no criticar”
MATEMÁTICA
9
“Hermana de la salud es la alegría”
JRC
INTERVALOS
Son todos aquellos subconjuntos especiales de números reales, los cuales pueden graficarse en la recta
numérica real.
CLASES.- Los intervalos se clasifican en intervalos limitados e ilimitados
A) INTERVALOS LIMITADOS.- Se tiene los siguientes:
1)
INTERVALO ABIERTO POR LA IZQUIERDA Y DERECHA.- Si a y b son números reales
Notación simbólica: ]a, b[ , se lee: “Intervalo abierto en a y b”.
b
L.
C
a
OM
entonces intervalo abierto en a y b son todos los números comprendidos entre a y b.
2)
NI
A
También: x ∈]a , b[ = {x ∈ R / a < x < b} notación conjuntista
INTERVALO CERRADO POR LA IZQUIERDA Y DERECHA.- Si a y b son números reales,
entonces intervalo cerrado en a y b son todos los números reales “x” e incluso a y b
DO
a
GE
Notación simbólica [a, b], se lee: “Intervalo cerrado en a y b”
b
También x ∈ [a , b] = {x ∈ R / a ≤ x ≤ b}
INTERVALO ABIERTO POR LA IZQUIERDA Y CERRADO POR LA DERECHA.- Si a y b son
.M
UN
3)
números reales, entonces intervalo abierto por la izquierda en a y cerrado en b, son todos los
números reales “x”, tal que a<x ≤ b.
W
W
W
Notación simbólica ]a, b], se lee: “Intervalo abierto en a y cerrado en b”.
4)
a
b
También: x ∈]a , b] = {x ∈ R / a < x ≤ b}
INTERVALO CERRADO POR LA IZQUIERDA Y ABIERTO POR LA DERECHA.- Si a y b son
números reales, entonces intervalo cerrado por la izquierda en a y abierto en b, son todos los
números reales “x”, tal que a a ≤ x < b .
Notación simbólica: [a; b[ = {x ∈ R / a ≤ x < b}
“El que trabaja puede pregonar lo que ha hecho; el qué nada
hace, debe callarse, y no criticar”
MATEMÁTICA
10
“Hermana de la salud es la alegría”
a
JRC
b
B) INTERVALOS ILIMITADOS.- Se tiene los siguientes:
1)
INTERVALO ABIERTO POR LA IZQUIERDA E INFINITO A LA DERECHA.- Son todos los
números mayores que “a”, tal que a < x y b ∈ R .
Notación simbólica: x ∈]a; ∞[ = {x ∈ R / a < x} “Intervalo abierto en a por la izquierda e
infinito por la derecha”.
Graficar: x ∈] − 3; ∞[= {x ∈ R / − 3 < x}
OM
EJEMPLO:
∞
a
SOLUCIÓN: Se tiene:
2)
L.
C
− 3
∞
INTERVALO INFINITO A LA IZQUIERDA Y ABIERTO POR LA DERECHA.- Son todos los
NI
A
números menores que b, tal que x < b y b ∈ R
Notación simbólica: x ∈] − ∞; b[ = {x ∈ R / x < b} “Intervalo infinito a la izquierda y abierto
por la derecha en b”.
x ∈] − ∞;3[ = {x ∈ R / x < 3}
GE
EJEMPLO:
3)
DO
solución
−∞
∞
3
INTERVALO CERRADO POR LA IZQUIERDA E INFINITO A LA DERECHA.- Son todos los
.M
UN
números reales mayores o igual que a, tal que a ≤ x y a ∈ R .
Notación simbólica: x ∈ [a; ∞[ = {x ∈ R / a ≤ x} “Intervalo cerrado en a por la izquierda e
infinito a la derecha”.
∞
a
INTERVALO INFINITO A LA IZQUIERDA Y CERRADO POR LA DERECHA.- Son todos los
W
4)
W
−∞
W
números reales menores o igual que b, tal que x ≤ b y b ∈ R .
Notación simbólica: x ∈ [−∞; b[ = {x ∈ R / x ≤ b} “Intervalo infinito a la izquierda y cerrado en
b por la derecha”
−∞
b
1
1
EJEMPLO: Graficar: x ∈ [−∞;− [= {x ∈ R / x ≤ − }
2
2
SOLUCIÓN: Se tiene:
“El que trabaja puede pregonar lo que ha hecho; el qué nada
hace, debe callarse, y no criticar”
MATEMÁTICA
11
“Hermana de la salud es la alegría”
−∞
....
-4
-3
-2
-1
0
JRC
1
2
...
∞
EJERCICIOS
COLOCAR VERDADERO (V) O FALSO (F) DESPUÉS DE ANALIZAR CUIDADOSAMENTE LOS
1)
] − 5;6] = {x ∈ R / − 5 < x < 6}
( )
2)
[3; ∞[ = {n ∈ R / 3 < n}
( )
3)
] − ∞;−3[= { y ∈ R / y ≤ −3}
( )
4)
[ 6 ; ∞[= {x ∈ R / 6 ≤ x}
( )
OM
SIGUIENTES EJERCICIOS:
Infinito por la izquierda y cerrado por la derecha.
6)
Abierto por la izquierda e infinito por la derecha
7)
Cerrado por la izquierda y derecha
8)
Abierto por la izquierda y cerrado por la derecha
9)
Abierto por la izquierda y derecha
] − ∞;− 26 ]
................................
NI
A
5)
L.
C
COLOCAR UN EJEMPLO, CON NOTACIÓN DE INTERVALO:
.................................
GE
.................................
..................................
..................................
11) Infinito por la izquierda y abierto por la derecha
.................................
12) Abierto por la izquierda y derecha
..................................
DO
10) Cerrado por la izquierda e infinito por la derecha
=
] − ∞;−8]
14) {m ∈ R / m ≥ 5}
=
......................
15) {n ∈ R / 1 < n ≤ 2}
=
......................
16) {x ∈ R / − 0,5 < x}
=
......................
17) {x ∈ R / 2 < x < 3}
=
......................
18) { y ∈ R / − 3 < y}
=
......................
19) {m ∈ R / − 8 ≤ m < 8}
=
......................
1
5
20) {t ∈ R / ≤ t ≤ }
3
4
=
......................
W
W
13) {x ∈ R / x ≤ −8}
W
.M
UN
LOS SIGUIENTES CONJUNTOS EXPRESAR EN FORMA DE INTERVALO.
COMPLETAR EN LOS ESPACIOS VACÍOS:
REPRESENTACIÓN GRAFICA
NOTACIÓN
NOTACIÓN
SIMBÓLICA
CONJUNTISTA
[ −3;2[
{x ∈ R / − 3 ≤ x < 2}
“El que trabaja puede pregonar lo que ha hecho; el qué nada
hace, debe callarse, y no criticar”
MATEMÁTICA
12
“Hermana de la salud es la alegría”
1
] ;18]
2
JRC
{y ∈ R /
1
< y ≤ 18}
2
] − ∞;6]
[3; ∞[
{m ∈ R / m ≥ 3}
4
] ; ∞[
5
[ −5;1,5]
L.
C
∞
OM
{x ∈ R / − 25 ≤ x ≤ 25}
{x ∈ R / x ≥ 9}
NI
A
] − 2; ∞[
{x ∈ R / − 3 < x ≤ 2}
GE
OPERACIONES CON INTERVALOS: REUNIÓN, INTERSECCIÓN Y DIFERENCIA.- Para resolver
operaciones con intervalos es recomendable graficarlos con la finalidad de hacer más sencillo las
1)
EJEMPLOS:
DO
operaciones.
Dados M = [3; 6[ ; N = ]5; ∞[ , hallar:
b) M ∩ N
.M
UN
a) M ∪ N
SOLUCIÓN
c) M − N
d) N − M
Completar y señalar la respuesta.
W
a) M ∪ N =
3
4
5
6
7
8
3
4
5
6
7
8
W
W
b) M ∩ N =
c) M − N =
3
4
5
6
7
8
3
4
5
6
7
8
d) N − M =
“El que trabaja puede pregonar lo que ha hecho; el qué nada
hace, debe callarse, y no criticar”
MATEMÁTICA
13
“Hermana de la salud es la alegría”
JRC
EJERCICIOS
1) Colocar verdadero (V) o falso (F) después de analizar cuidadosamente los siguientes ejercicios:
a)
]2;3[∪]2;5] = ]2;5]
(
)
b)
[ −5;1] ∪ [1;2] = [1;3]
(
)
c)
[ −5;−3] ∩ [ −2;5] = φ
d)
[2;8] − [2;8] = φ
(
)
e)
[ −6;−1] ∩ [0,1] = [ −1;0]
(
)
f)
[0,5;1] − [5;5,5] = φ
(
)
a)
] − ∞;4[∪] − ∞; ∞[ =
b)
[5;6] ∪ [4;1]
c)
[ −10;0]∪] − 6;0[
d)
]5;8[∩]6;9[
NI
A
2) Resolver las siguientes operaciones y representar gráficamente.
OM
)
L.
C
(
=
W
W
W
.M
UN
=
DO
GE
=
e)
[ −6;3] ∩ [−6;−2]
=
f)
] − 4;2]− ]0;4]
=
“El que trabaja puede pregonar lo que ha hecho; el qué nada
hace, debe callarse, y no criticar”
MATEMÁTICA
14
“Hermana de la salud es la alegría”
JRC
] − ∞;1] − [0;6] =
1)
Representa en la recta real y escribe con notación de intervalos
Calcula y representa en la recta real.
]− 4;4]∩ ]0;6[
W
W
W
a)
.M
UN
2)
DO
GE
NI
A
A = {x x ∈ R;1 / 2 < x ≤ 3}
L.
C
OM
g)
b)
]− 4;4] − [− 2;5]
“El que trabaja puede pregonar lo que ha hecho; el qué nada
hace, debe callarse, y no criticar”
MATEMÁTICA
4)
JRC
Expresa la inecuación correspondiente.
a)
[− 4;+∞[
b)
[− 4;+3[
OM
3)
15
“Hermana de la salud es la alegría”
Determine el intervalo al que pertenece x.
Dados los conjuntos
A = {x / − 4 ≤ x ≤ 5}
DO
5)
GE
NI
A
L.
C
( x + 2) ∈ ]− 5;3]
A–B
Dados los conjuntos
W
6)
W
.M
UN
Halla y representa en la recta numérica.
B = {x / − 7 ≤ x < −1}
A = {x / − 4 ≤ x ≤ 5}
W
Halla y representa en la recta numérica.
7)
B = {x / − 7 ≤ x < −1}
A∪ B
Continúa la solución aplicando las propiedades de valor absoluto.
“El que trabaja puede pregonar lo que ha hecho; el qué nada
hace, debe callarse, y no criticar”
MATEMÁTICA
16
“Hermana de la salud es la alegría”
JRC
8)
OM
2 x − 3 = 15
Resuelve la siguiente ecuación aplicando las propiedades de valor absoluto.
Continúa la solución aplicando las propiedades de valor absoluto
.M
UN
9)
DO
GE
NI
A
L.
C
x−3
−3 = 0
3
W
W
W
2X + 4 = 6 − X
10) Resuelve la siguiente ecuación aplicando las propiedades de valor absoluto.
X
+6 −3= 0
3
“El que trabaja puede pregonar lo que ha hecho; el qué nada
hace, debe callarse, y no criticar”
17
“Hermana de la salud es la alegría”
11) Halla el conjunto solución de la siguiente inecuación
GE
NI
A
L.
C
6x − 2 < 2x + 6
JRC
OM
MATEMÁTICA
W
.M
UN
6x − 2 ≤ 2x + 6
DO
12) Halla el conjunto solución de la siguiente inecuación
W
13) Halla el conjunto solución de la siguiente inecuación
W
6x − 2 > 2x + 6
14) Halla el conjunto solución de la siguiente inecuación
6x − 2 ≥ 2x + 6
“El que trabaja puede pregonar lo que ha hecho; el qué nada
hace, debe callarse, y no criticar”
MATEMÁTICA
18
“Hermana de la salud es la alegría”
OM
15) Halla el conjunto solución de la siguiente inecuación
JRC
GE
NI
A
L.
C
6x − 2 < 2x + 8
W
.M
UN
4x − 2 ≤ 2x + 6
DO
16) Halla el conjunto solución de la siguiente inecuación
17) Halla el conjunto solución de la siguiente inecuación
W
W
6 x − 2 > 3x + 9
18) Halla el conjunto solución de la siguiente inecuación
6 x − 4 ≥ 2 x + 10
“El que trabaja puede pregonar lo que ha hecho; el qué nada
hace, debe callarse, y no criticar”
19
“Hermana de la salud es la alegría”
JRC
NI
A
L.
C
OM
MATEMÁTICA
GE
RESUELVE EN TU CUADERNO
RESOLVER LAS ECUACIONES:
6.
4X = 8
2.
− X + 4 =1
7.
2X +1 = X
3.
2X −1 = X +1
8.
5 − 4X = X
4.
3X − 8 = X + 2
9.
2X + 3 = 8
5.
4X + 7 = X − 2
10. 10 − 7 X = − 3 − 2 X
DO
X =6
W
W
.M
UN
1.
W
RESOLVER LAS INECUACIONE
11. 4 X − 8 < 3 X + 7
16. − X + 8 ≤ 2 X − 15 < 20 + 3 X
12. 5 X − 3 > −2 X + 8
17. − 2 X + 3 ≥ 8 − X > 3 X − 5
13. 6 X + 7 ≥ 2 X + 11
18. 2 X − 1 < 4 X − 3 < X − 9
14. X − 9 < 4 X − 3 < 2 X − 1
19. 3 X − 5 ≥ 2 X + 4 ≥ X − 5
15. X − 3 < 2 X − 1 < 3 X + 7
20. X − 5 > 2 X + 4 > 3 X − 5
“El que trabaja puede pregonar lo que ha hecho; el qué nada
hace, debe callarse, y no criticar”
MATEMÁTICA
20
“Hermana de la salud es la alegría”
JRC
21. X < 6
31. 4 X > 8
22. − X + 4 ≤ 1
32. 2 X + 1 < X
23. 2 X − 1 > X + 1
33. 5 − 4 X < 5
24. 3 X − 8 ≥ X + 2
34. 2 X + 3 > 8
25. 4 X + 7 ≤ X − 2
35. 10 − 7 X ≥ 4
L.
C
26. X + 3 ≤ 4
OM
RESOLVER LAS INECUACIONES
27. 5 − X ≤ 7
NI
A
28. 2 X + 1 ≤ 3 X − 4
29. 3 X + 2 < 4 X − 1
W
W
W
.M
UN
DO
GE
30. 10 − X ≥ 3 X − 1
“El que trabaja puede pregonar lo que ha hecho; el qué nada
hace, debe callarse, y no criticar”