Taller de Cálculo Integral: Sólidos de Revolución

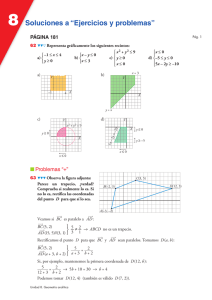
Taller de Cálculo Integral: Sólidos de Revolución
Presentado por:
Luis Mojica Cod. 1153934
El área acotada por la curva
y la recta
genera varios sólidos de
revolución cuando gira
a.) Alrededor del eje
b.) Alrededor de la recta
c.) Alrededor del eje
d.) Alrededor de la recta
e.) Alrededor de la recta
Hallar el volumen generado en cada caso.
a.) Alrededor del eje
b.) Alrededor de la recta
Desplazamos
reflejamos
la
el
sistema
función
de
respecto
coordenadas,
al
eje
y
aprovechamos la simetría de la función respecto al
eje
Nueva función:
.
c.) Alrededor del eje
Utilizamos el método de las arandelas y de nuevo
aprovechamos la simetría de la función respecto al
eje
.
d.) Alrededor de la recta
Desplazamos el sistema de coordenadas y
utilizamos el mismo método que en el numeral
anterior.
Nuevas funciones:
e.) Alrededor de la recta
Desplazamos el sistema de coordenadas
así:
Nueva función:
Fin.