PRUEBA Nº 1 - fisica-2

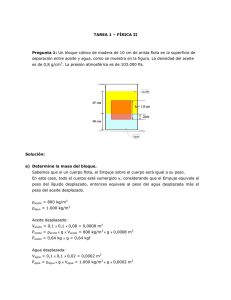
INGENIERÍA EN CONSTRUCCIÓN - IPLA
RESPUESTAS PRUEBA Nº 1
FÍSICA DE FLUIDOS
Pregunta 1: Un cubo de madera de corcho tiene 20 cm de arista y pesa 6 kgf.
1.1 Determine si el cubo flota cuando se introduce en el agua y explicar por qué, en
caso afirmativo.
Si el peso del cubo es menor al empuje que el agua ejerce sobre él, el cubo flotará, pero si su
peso es mayor, el cubo se hundirá.
Una forma fácil de averiguar si el cubo flota, es sencillamente calculando su densidad y
comparándola con la densidad del agua; así, si su densidad es menor a la del agua, flotará y
en caso contrario se hundirá.
Calculemos la densidad del cubo:
Como el cubo pesa 6 kgf, su masa M será de 6 kg
ρcubo = Mcubo
Vcubo = 0,2x0,2x0,2 m3 = 0,008 m3
Vcubo
ρcubo =
6 kg
ρcubo = 750 kg/m3
0,008 m3
Como ρagua = 1.000 kg/m3,
ρcubo < ρagua
por lo tanto, flota
1.2 Calcular el volumen de agua desplazado al flotar.
El Empuje deberá ser igual al peso del cubo para que se mantenga a flote, así:
E = ρaguaxgxVS = 6 kgf
(g: aceleración de gravedad)
Supongamos X = 0,2 m – Y
(o sea, X es la profundidad sumergida del cubo)
VS = 0,2x0,2xX = 0,04xX m3
E = 1.000 kg/m3xgx0,04xX m3 = 6 kgxg
despejamos m3, kg y g
40xX = 6
X = 0,15 m
Finalmente:
VS = 0,2 mx0,2 mx0,15 m = 0,006 m3
(se considera que X está en metros)
INGENIERÍA EN CONSTRUCCIÓN - IPLA
1.3 Calcular el volumen emergente del cubo.
El volumen total del cubo es el volumen emergente más el volumen sumergido:
Vcubo = VE + VS
0,008 m3 = VE + 0,006 m3
VE = 0,002 m3
Pregunta 2: El líquido del manómetro de tubo abierto de la figura es mercurio (Hg), y
dentro del depósito hay aire comprimido. La presión atmosférica es de 100.000 Pa.
2.1 Calcular la presión absoluta en el fondo del tubo en U (Pa).
La presión absoluta es la presión manométrica más la presión atmosférica:
PABS = PMAN + PATM
Por otro lado, la densidad del mercurio es de 13.600 kg/m3
En el fondo del tubo:
PMAN = 13.600 kg/m3x0,10 mxg = 1.360 kg/m2xg = 1.360 kgf/m2
a un kg de masa multiplicado por g)
(recuerden, 1 kgf es igual
PMAN = 1.360 kgf/m2 = 13.600 N/m2 = 13.600 Pa
(también recuerden que 1 kgf equivale a 10 N y que 1 Pa es igual a 1 N/m2)
Luego,
PABS = 13.600 Pa + 100.000 Pa = 113.600 Pa
en el fondo del tubo en U
2.2 Calcular la presión absoluta en el tubo abierto a 6 cm de la superficie libre (Pa).
PABS = PMAN + PATM
PMAN = 13.600 kg/m3x0,06 mxg = 816 kg/m2xg = 816 kgf/m2
PMAN = 8.160 N/m2 = 8.160 Pa
Luego,
PABS = 8.160 Pa + 100.000 Pa = 108.160 Pa
a 6 cm de la superficie libre
2.3 Calcular la presión absoluta del gas en el depósito (Pa).
La presión absoluta del mercurio calculada en el punto anterior es para 6 cm bajo la superficie
libre. A ese mismo nivel, el mercurio toma contacto con el aire comprimido y como a un mismo
nivel las presiones de un líquido son iguales, en ese punto la presión absoluta será de 108.160
INGENIERÍA EN CONSTRUCCIÓN - IPLA
Pa. Además, como la presión de un gas es la misma en todo el volumen que ocupa, la presión
en el depósito será también de 108.160 Pa.
2.4 Calcular la presión manométrica del aire comprimido (Pa).
La presión manométrica corresponde a la presión absoluta menos la presión atmosférica, por
lo que
PABS - PATM = PMAN
108.160 Pa – 100.000 Pa = 8.160 Pa
Otra forma de resolverlo, es decir que la presión manométrica a 6 cm de la superficie libre
será la misma que en el punto donde el mercurio toma contacto con el aire comprimido. Esta
presión se calculó en 2.2:
PMAN = 8.160 Pa
2.5 Calcular la presión manométrica del aire comprimido en cm de Hg.
Simplemente equivale a la diferencia de niveles o cotas entre las dos superficies del mercurio:
10 cm – 4 cm = 6 cm
Se dice que el aire comprimido ejerció suficiente presión como para “empujar” el mercurio
esos 6 cm a través del tubo.
Pregunta 3:
3.1 Explique el funcionamiento de la máquina hidráulica de la figura a), que permite
mover un peso varias veces superior a la fuerza aplicada.
La máquina hidráulica es simplemente un vaso comunicante en donde las presiones son
iguales a un mismo nivel. Esto significa que P1 = P2, entonces F1/A1 = F2/A2
Si el pistón 2 es, digamos, 40 veces más grande que el de la izquierda, tendremos A 2 = 40xA1.
Como las presiones en ambos pistones es la misma, F1/A1 = F2/(40xA1)
F2=F1x(40xA1/A1)
F2 = 40xF1
Esto significa que la fuerza que aplique sobre el pistón 1 se va a multiplicar cuarenta veces en
el pistón 2, lo que me permitirá mover objetos pesados, como vehículos.
INGENIERÍA EN CONSTRUCCIÓN - IPLA
3.2 Explique el funcionamiento del sifón de la figura b). Considere que entre A y B
hay menos de 10 m de cota.
No importa la forma que tenga el sifón, si existe un desnivel entre la superficie libre del
recipiente y el extremo libre de la manguera, existirá una diferencia de presión hidrostática
que hará que el recipiente se vacie hasta que el extremo libre de la manguera quede al mismo
nivel que la superficie libre del recipiente, pues en ese momento su presión será igual a la
presión atmosférica.
3.3 Explique el concepto de capilaridad.
Capilaridad es un fenómeno que ocurre cuando las fuerzas de adhesión de las moléculas de
agua sobre las moléculas de otro objeto son mayores a las fuerzas de cohesión entre las
mismas moléculas de agua. De este modo, el agua puede “ascender” por distintos materiales.
3.4 Enuncie las leyes de Boyle y de Gay-Lussac.
Ley de Boyle:
El volumen de un gas a temperatura constante es inversamente proporcional a la presión.
p1.V1 = p2.V2
Ley de Gay-Lussac:
a) El volumen de un gas a presión constante es directamente proporcional a la temperatura
absoluta.
V1/T1 = V2/T2
b) Otra ley afirma que a volumen constante la presión es directamente proporcional a la
temperatura absoluta.
p1/T1 = p2/T2