TAREA 1 - 2009 FÍSICA DE FLUIDOS Pregunta 1: Un cubo de
Anuncio

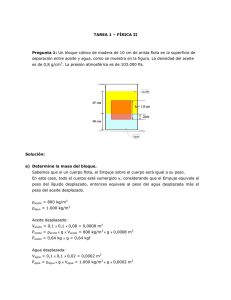
FÍSICA II – ING. EN AGROINDUSTRIAS IPLA - 2012 TAREA 1 - 2009 FÍSICA DE FLUIDOS Pregunta 1: Un cubo de madera de corcho tiene 20 cm de arista y pesa 6 kgf. 1.1 Determine si el cubo flota cuando se introduce en el agua y explicar por qué, en caso afirmativo. Si el peso del cubo es menor al empuje que el agua ejerce sobre él, el cubo flotará, pero si su peso es mayor, el cubo se hundirá. Una forma fácil de averiguar si el cubo flota, es sencillamente calculando su densidad y comparándola con la densidad del agua; así, si su densidad es menor a la del agua, flotará y en caso contrario se hundirá. Calculemos la densidad del cubo: Como el cubo pesa 6 kgf, su masa M será de 6 kg Vcubo = 0,2x0,2x0,2 m3 = 0,008 m3 ρcubo = Mcubo Vcubo ρcubo = ρcubo = 750 kg/m3 6 kg 0,008 m3 Como ρagua = 1.000 kg/m3, ρcubo < ρagua por lo tanto, flota 1.2 Calcular el volumen de agua desplazado al flotar. El Empuje deberá ser igual al peso del cubo para que se mantenga a flote, así: E = ρaguaxgxVS = 6 kgf (g: aceleración de gravedad) Supongamos X = 0,2 m – Y VS = 0,2x0,2xX = 0,04xX m (o sea, X es la profundidad sumergida del cubo) 3 E = 1.000 kg/m3xgx0,04xX m3 = 6 kgxg despejamos m3, kg y g 40xX = 6 X = 0,15 m Finalmente: VS = 0,2 mx0,2 mx0,15 m = 0,006 m3 (se considera que X está en metros) FÍSICA II – ING. EN AGROINDUSTRIAS IPLA - 2012 1.3 Calcular el volumen emergente del cubo. El volumen total del cubo es el volumen emergente más el volumen sumergido: Vcubo = VE + VS 0,008 m3 = VE + 0,006 m3 VE = 0,002 m3 Pregunta 2: El líquido del manómetro de tubo abierto de la figura es mercurio (Hg), y dentro del depósito hay aire comprimido. La presión atmosférica es de 100.000 Pa. 2.1 Calcular la presión absoluta en el fondo del tubo en U (Pa). La presión absoluta es la presión manométrica más la presión atmosférica: PABS = PMAN + PATM Por otro lado, la densidad del mercurio es de 13.600 kg/m3 En el fondo del tubo: PMAN = 13.600 kg/m3x0,10 mxg = 1.360 kg/m2xg = 1.360 kgf/m2 un kg de masa multiplicado por g) (recuerden, 1 kgf es igual a PMAN = 1.360 kgf/m2 = 13.600 N/m2 = 13.600 Pa (también recuerden que 1 kgf equivale a 10 N y que 1 Pa es igual a 1 N/m2) Luego, PABS = 13.600 Pa + 100.000 Pa = 113.600 Pa en el fondo del tubo en U 2.2 Calcular la presión absoluta en el tubo abierto a 6 cm de la superficie libre (Pa). PABS = PMAN + PATM PMAN = 13.600 kg/m3x0,06 mxg = 816 kg/m2xg = 816 kgf/m2 PMAN = 8.160 N/m2 = 8.160 Pa Luego, PABS = 8.160 Pa + 100.000 Pa = 108.160 Pa a 6 cm de la superficie libre 2.3 Calcular la presión absoluta del gas en el depósito (Pa). La presión absoluta del mercurio calculada en el punto anterior es para 6 cm bajo la superficie libre. A ese mismo nivel, el mercurio toma contacto con el aire comprimido y como a un mismo FÍSICA II – ING. EN AGROINDUSTRIAS IPLA - 2012 nivel las presiones de un líquido son iguales, en ese punto la presión absoluta será de 108.160 Pa. Además, como la presión de un gas es la misma en todo el volumen que ocupa, la presión en el depósito será también de 108.160 Pa. 2.4 Calcular la presión manométrica del aire comprimido (Pa). La presión manométrica corresponde a la presión absoluta menos la presión atmosférica, por lo que PABS - PATM = PMAN 108.160 Pa – 100.000 Pa = 8.160 Pa Otra forma de resolverlo, es decir que la presión manométrica a 6 cm de la superficie libre será la misma que en el punto donde el mercurio toma contacto con el aire comprimido. Esta presión se calculó en 2.2: PMAN = 8.160 Pa 2.5 Calcular la presión manométrica del aire comprimido en cm de Hg. Simplemente equivale a la diferencia de niveles o cotas entre las dos superficies del mercurio: 10 cm – 4 cm = 6 cm Se dice que el aire comprimido ejerció suficiente presión como para “empujar” el mercurio esos 6 cm a través del tubo. Pregunta 3: 3.1 Explique el funcionamiento de la máquina hidráulica de la figura a), que permite mover un peso varias veces superior a la fuerza aplicada. La máquina hidráulica es simplemente un vaso comunicante en donde las presiones son iguales a un mismo nivel. Esto significa que P1 = P2, entonces F1/A1 = F2/A2 Si el pistón 2 es, digamos, 40 veces más grande que el de la izquierda, tendremos A2 = 40xA1. Como las presiones en ambos pistones es la misma, F1/A1 = F2/(40xA1) F2=F1x(40xA1/A1) F2 = 40xF1 Esto significa que la fuerza que aplique sobre el pistón 1 se va a multiplicar cuarenta veces en el pistón 2, lo que me permitirá mover objetos pesados, como vehículos. FÍSICA II – ING. EN AGROINDUSTRIAS IPLA - 2012 3.2 Explique el funcionamiento del sifón de la figura b). Considere que entre A y B hay menos de 10 m de cota. No importa la forma que tenga el sifón, si existe un desnivel entre la superficie libre del recipiente y el extremo libre de la manguera, existirá una diferencia de presión hidrostática que hará que el recipiente se vacie hasta que el extremo libre de la manguera quede al mismo nivel que la superficie libre del recipiente, pues en ese momento su presión será igual a la presión atmosférica. FÍSICA II – ING. EN AGROINDUSTRIAS IPLA - 2012 TAREA 1 - 2010 FÍSICA II Pregunta 1: Una morsa se encuentra sobre un bloque de hielo en el Ártico. La densidad del agua de mar es de 1.040 kg/m3 y la densidad del hielo es de 980 kg/m3 y el volumen emergente del hielo es de 1 m3. Si el volumen emergente del hielo es una vigésima parte del volumen sumergido, calcule: 1.1 El peso del bloque de hielo. 1.2 El peso de la morsa. Solución: 1.1 El peso del bloque de hielo. Sabemos que el volumen emergente del hielo (VE) es una vigésima parte del volumen sumergido (VS), es decir, VE = VS/20. Si VE = 1 m3, tenemos: 1 m3 = VS/20 20 x 1 m3 = VS 20 m3 = VS Como VT = VE + VS, VT = 1 m3 + 20 m3 VT = 21 m3 Finalmente, para sacar el peso del bloque de hielo: PH = ρhielo x VT x g PH = 980 kg/m3 x 21 m3 x g PH = 980 kg/m3 x 21 m3 x g PH = 20.580 kgf FÍSICA II – ING. EN AGROINDUSTRIAS IPLA - 2012 1.2 El peso de la morsa. Para que el bloque de hielo se mantenga a flote, el Empuje del agua debe ser igual al peso total del bloque de hielo más el peso de la morsa. PH + Pmorsa = E Además, E = ρagua de mar x VS x g E = 1.040 kg/m3 x 20 m3 x g E = 20.800 kgf Luego: 20.580 kgf + Pmorsa = 20.800 kgf Pmorsa = 220 kgf Si lo expresamos en masa: Pmorsa = 220 kg x g Mmorsa = 220 kg Pregunta 2: Los líquidos del manómetro de tubo abierto de la figura son mercurio (13.600 kg/m3), y glicerina (1.250 kg/m3), respectivamente; dentro del depósito hay un gas comprimido. La presión atmosférica es de 103.000 Pa. 2.1 Calcular la presión absoluta en el tubo abierto a 16 cm de la superficie libre (Pa). 2.2 Calcular la presión absoluta del gas en el depósito (Pa). 2.3 Si a presión atmosférica el gas tiene un volumen de 0,09 m3, calcule el volumen del gas dentro del depósito en las condiciones actuales. Considere que la temperatura se mantiene constante. FÍSICA II – ING. EN AGROINDUSTRIAS IPLA - 2012 Solución: 2.1 Calcular la presión absoluta en el tubo abierto a 16 cm de la superficie libre (Pa). PABS = PMAN + PATM PMAN = 1.250 kg/m3x0,16 m x g = 200 kg/m2xg = 200 kgf/m2 PMAN = 2.000 N/m2 = 2.000 Pa Luego, PABS = 2.000 Pa + 103.000 Pa = 105.000 Pa a 16 cm de la superficie libre 2.2 Calcular la presión absoluta del gas en el depósito (Pa). La presión absoluta calculada en el punto anterior es para 16 cm bajo la superficie libre, en donde se encuentran la glicerina y el mercurio. A ese mismo nivel, el mercurio toma contacto con el aire comprimido y como a un mismo nivel las presiones de un líquido son iguales, en ese punto la presión absoluta será de 105.000 Pa. Además, como la presión de un gas es la misma en todo el volumen que ocupa, la presión en el depósito será también de 105.000 Pa. FÍSICA II – ING. EN AGROINDUSTRIAS IPLA - 2012 TAREA 2 - 2009 FÍSICA DE FLUIDOS Pregunta 1: Un grupo de scout trata de construir una balsa y recorrer un río tranquilo. La masa de los scout y su equipo es de 400 kg. Los troncos disponibles tienen un diámetro promedio de 20 cm y una densidad de 800 kg/m3. Ellos le piden determinar el área mínima de la balsa de troncos que les permita flotar sin mojarse. Solución: Para que la balsa se mantenga a flote, el Empuje debe ser IGUAL al peso total de los troncos y de los scout con su equipo. Por simplicidad, se puede considerar un único tronco de longitud L y de diámetro D = 20 cm. Vtr = ∏ x r2 x L Volumen tronco r = 0,1 m Radio del tronco ρagua = 1.000 kg/m3 ρtr = 800 kg/m 3 E = ρagua g x Vtr x Densidad del tronco Pscout = 400 kgf Ptr = ρtr x Vtr x Densidad del agua La masa de los scout y su equipo es de 400 kg, lo cual pesa 400 kgf g E = Pscout + Ptr ρagua x ρagua x Vtr g - ρtr x Vtr Vtr Vtr x g = 400 kgf + ρtr x x x Vtr x x r2 x L, x g g = 400 kgf = 400 kg (ρagua - ρtr) = 400 kg x 200 kg/m3 = 400 kg Vtr = 400 m3 200 Vtr = 2 m3 Vtr = ∏ Vtr (1.000 kg/m3 – 800 kg/m3) = 400 kg Vtr Como x x g FÍSICA II – ING. EN AGROINDUSTRIAS IPLA - 2012 Vtr = ∏ ∏ x r2 (0,1 m)2 x 3,1416 x L = 2 m3 x x L = 2 m3 0,01 m2 0,031416 x x L = 2 m3 L=2m L = 63,66 m Finalmente, el área del tronco será L x D: A=L x D = 63,66 m x 0,2 m A = 12,73 m2 Pregunta 2: Los líquidos del manómetro de tubo abierto de la figura son mercurio (13.600 kg/m3), y glicerina (1.250 kg/m3), respectivamente; dentro del depósito hay un gas comprimido. La presión atmosférica es de 100.000 Pa. 2.1 Calcular la presión absoluta en el fondo del tubo en U (Pa). 2.2 Calcular la presión absoluta en el tubo abierto a 16 cm de la superficie libre (Pa). 2.3 Calcular la presión absoluta del gas en el depósito (Pa). 2.4 Calcular la presión manométrica del gas comprimido (Pa). Solución: 2.1 Calcular la presión absoluta en el fondo del tubo en U (Pa). La presión absoluta es la presión manométrica más la presión atmosférica: PABS = PMAN + PATM Por otro lado, la densidad del mercurio es de 13.600 kg/m3 y la de la glicerina es de 1.250 kg/m3. En el fondo del tubo: PMAN = 1.250 kg/m3x0,16 m x g + 13.600 kg/m3 x 0,03 m x g = 200 kg/m2 x g + 408 kg/m2 x g PMAN = 608 kgf/m2 (recuerden, 1 kgf es igual a un kg de masa multiplicado por g) PMAN = 608 kgf/m2 = 6.080 N/m2 = 6.080 Pa (también recuerden que 1 kgf equivale a 10 N y que 1 Pa es igual a 1 N/m2) Luego, FÍSICA II – ING. EN AGROINDUSTRIAS IPLA - 2012 PABS = 6.080 Pa + 100.000 Pa = 106.080 Pa en el fondo del tubo en U 2.2 Calcular la presión absoluta en el tubo abierto a 16 cm de la superficie libre (Pa). PABS = PMAN + PATM PMAN = 1.250 kg/m3x0,16 m x g = 200 kg/m2xg = 200 kgf/m2 PMAN = 2.000 N/m2 = 2.000 Pa Luego, PABS = 2.000 Pa + 100.000 Pa = 102.000 Pa a 16 cm de la superficie libre 2.3 Calcular la presión absoluta del gas en el depósito (Pa). La presión absoluta calculada en el punto anterior es para 16 cm bajo la superficie libre, en donde se encuentran la glicerina y el mercurio. A ese mismo nivel, el mercurio toma contacto con el aire comprimido y como a un mismo nivel las presiones de un líquido son iguales, en ese punto la presión absoluta será de 102.000 Pa. Además, como la presión de un gas es la misma en todo el volumen que ocupa, la presión en el depósito será también de 102.000 Pa. 2.4 Calcular la presión manométrica del aire comprimido (Pa). La presión manométrica corresponde a la presión absoluta menos la presión atmosférica, por lo que PABS - PATM = PMAN 102.000 Pa – 100.000 Pa = 2.000 Pa Otra forma de resolverlo, es decir que la presión manométrica a 16 cm de la superficie libre será la misma que en el punto donde el mercurio toma contacto con el aire comprimido. Esta presión se calculó en 2.2: PMAN = 2.000 Pa FÍSICA II – ING. EN AGROINDUSTRIAS IPLA - 2012 TAREA 2 – FÍSICA II - 2010 Pregunta 1: Un bloque cúbico de madera de 10 cm de arista flota en la superficie de separación entre aceite y agua, como se muestra en la figura. La densidad del aceite es de 0,8 g/cm3. La presión atmosférica es de 103.000 Pa. Solución: a) Determine la masa del bloque. Sabemos que si un cuerpo flota, el Empuje sobre el cuerpo será igual a su peso. En este caso, todo el cuerpo está sumergido y, considerando que el Empuje equivale al peso del líquido desplazado, entonces equivale al peso del agua desplazada más el peso del aceite desplazado. ρaceite = 800 kg/m3 ρagua = 1.000 kg/m3 Aceite desplazado: Vaceite = 0,1 x 0,1 x 0,08 = 0,0008 m3 Paceite = ρaceite x g x Vaceite = 800 kg/m3 x g x 0,0008 m3 Paceite = 0,64 kg x g = 0,64 kgf Agua desplazada: Vagua = 0,1 x 0,1 x 0,02 = 0,0002 m3 Pagua = ρagua x g x Vagua = 1.000 kg/m3 x g x 0,0002 m3 Pagua = 0,2 kg x g = 0,2 kgf FÍSICA II – ING. EN AGROINDUSTRIAS IPLA - 2012 Luego, E = Pcubo E = Paceite + Pagua Igualando ambas ecuaciones, se tiene: Pcubo = Paceite + Pagua Pcubo = 0,64 kgf + 0,2 kgf Pcubo = 0,84 kgf El peso de un cuerpo equivale a su masa multiplicada por g. Pcubo = 0,84 kg x g = Mcubo x g Mcubo = 0,84 kg b) Determine la presión manométrica sobre la superficie inferior del bloque. Se debe determinar la presión en la interfaz y se le debe agregar la presión hidrostática de los 2 cm de agua. PMAN = 1.200 Pa + ρagua x g x hagua = 1.200 Pa + 1.000 kg/m3 x g x 0,02 m PMAN = 1.200 Pa + 200 Pa PMAN = 1.400 Pa c) Determine la presión manométrica en la interfaz. PMAN = ρaceite x g x haceite = 800 kg/m3 x g x 0,15 m PMAN = 1.200 Pa d) Determine la presión absoluta en la interfaz. PABS = PMAN + PATM PABS = 1.200 Pa + 103.000 Pa PABS = 104.200 Pa e) Determine la presión manométrica al fondo del recipiente. Se debe determinar la presión en la interfaz y se le debe agregar la presión hidrostática de los 10 cm de agua. PMAN = 1.200 Pa + ρagua x g x hagua = 1.200 Pa + 1.000 kg/m3 x g x 0,1 m PMAN = 1.200 Pa + 1.000 Pa PMAN = 2.200 Pa f) Determine la presión absoluta al fondo del recipiente. PABS = PMAN + PATM PABS = 2.200 Pa + 103.000 Pa PABS = 105.200 Pa FÍSICA II – ING. EN AGROINDUSTRIAS IPLA - 2012 EJERCICIOS DE HIDROSTÁTICA 1) Determinar la presión manométrica en Pa sobre una superficie sumergida a 6 m de profundidad en una masa de agua. Respuesta: 60.000 Pa 2) ¿A qué profundidad de un aceite, de densidad relativa 0,750, se producirá una presión de 280.000 Pa?. ¿A qué profundidad si el líquido es agua?. Respuesta: 37,3 m y 28,0 m 3) Un depósito cerrado contiene 60 cm de mercurio, 150 cm de agua y 240 cm de un aceite de densidad relativa 0,750, conteniendo aire el espacio sobre el aceite. Si la presión manométrica en el fondo del depósito es de 3 kgf/cm2, ¿cuál será la lectura manométrica en Pa en la parte superior del depósito?. Respuesta: 186.000 Pa 4) El depósito de la figura 1 contiene un aceite de densidad relativa 0,750. Determine la lectura del manómetro A en Pa. Respuesta: 871 Pa 5) Con referencia a la figura 2, ¿qué presión manométrica en Pa en A hará que la glicerina suba hasta el nivel B?. Las densidades del aceite y la glicerina son 832 kg/m3 y 1.250 kg/m3, respectivamente. Respuesta: 35.000 Pa Figura 1 Figura 2 EJERCICIOS DE EMPUJE 1) Un objeto pesa 30 kg en el aire y 19 kg sumergido en el agua. Determinar su volumen y su densidad relativa. Respuesta: V = 0,011 m³ y DR = 2,73 FÍSICA II – ING. EN AGROINDUSTRIAS IPLA - 2012 2) Un trozo de corcho de 40 cm ³ se coloca en éter (δ = 0,72 g/cm ³), si la densidad del corcho es de 0,24 g/cm ³, ¿qué volumen queda sumergido?. Respuesta: 13,3 cm ³ 3) Se sumerge un cuerpo en agua y recibe un empuje de 65 N, ¿qué empuje experimentará en éter (ρ = 0,72 gf/cm ³) y en ácido sulfúrico (ρ = 1,84 gf/cm ³)?. Respuesta: 45,9 N y 117,3 N 4) Un cuerpo pesa en el aire 2,746 N, en agua 1,863 N y en alcohol 2,059 N. ¿Cuál será la densidad del alcohol y del cuerpo?. Respuesta: 0,777 g/cm ³ y 3,11 g/cm ³ 5) Un cubo de aluminio (δ = 2,7 g/cm ³) de 4 cm de lado se coloca en agua de mar (δ = 1025 kg/m ³), ¿flota o se hunde?. Respuesta: Se hunde 6) Si el cubo del problema anterior se coloca en mercurio (δ = 13,6 g/cm ³), ¿flota o se hunde?. Respuesta: No se hunde