Plan de clase (4/5)
Anuncio

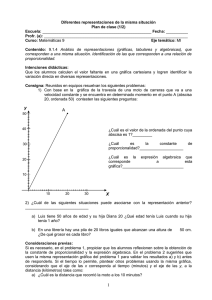
La misma para dos Plan de clase (1/2) Escuela: ________________________________________________ Fecha: ____________ Profesor (a): _______________________________________________________________ Curso: Matemáticas 3 Secundaria Eje temático: MI Contenido: 9.1.4 Análisis de representaciones (gráficas, tabulares y algebraicas) que corresponden a una misma situación. Identificación de las que corresponden a una relación de proporcionalidad. Intenciones didácticas: Que los alumnos identifiquen que hay varias situaciones que pueden ser modeladas por la misma gráfica y representación algebraica. Consigna: Reunidos en equipos resuelvan los siguientes problemas: 1) La siguiente es la gráfica de la distancia recorrida (representada con la letra y) por una moto de carreras en función del tiempo (representado con la letra x). La moto va a una velocidad constante y, en determinado momento, llega al punto A (20, 50). y A 50 40 ¿Cuál es el valor de la ordenada del punto cuya abscisa es 1 (x = 1)?_________ 30 ¿Cuál es la constante de proporcionalidad? __________ ¿Cuál es la expresión algebraica que corresponde a esta gráfica? _______________ 20 10 10 20 30 x 2) ¿A cuál de las siguientes situaciones corresponde la misma gráfica? a) La edad de Luis (y) respecto a la de su hija (x): Luis tiene 50 años de edad (y = 50) y su hija Diana 20 (x = 20). ¿Qué edad tenía Luis cuando su hija tenía 1 año? b) La altura de una pila de libros (y) respecto al número de libros (x): En una librería hay una pila de 20 libros iguales (x = 20) que alcanzan una altura de 50 cm (y = 50). ¿De qué grosor es cada libro? 1 3) Encuentren las representaciones algebraicas de las dos situaciones anteriores, (a) y (b). Consideraciones previas: El énfasis de la sesión se da al carácter abstracto de las representaciones algebraicas y de la gráfica cartesiana en términos de que a una misma expresión algebraica o a una misma gráfica corresponden diversas situaciones. Por ejemplo, la gráfica del problema señalado corresponde también a la altura de la pila de libros en función del número de libros (inciso b). Y la representación algebraica que les corresponde a ambas es: y = x. Si es necesario, ayude a que los alumnos reflexionen sobre la obtención de la constante de proporcionalidad y la expresión algebraica como se solicita en el problema. Para el problema 2, puede sugerirles que usen la representación gráfica del problema 1 para validar sus respuestas. Al observar que los valores que proporciona la gráfica no representan la relación entre las edades, los alumnos llegarán a la conclusión de que esta gráfica no corresponde al problema. La expresión correspondiente a la situación de las edades es: y = x + 30. Será importante que los alumnos expliquen lo que representa esta expresión en función de lo que indica el problema. Si el tiempo lo permite, plantee otros problemas del mismo tipo, es decir, diferentes situaciones a las que correspondan la misma gráfica y la misma expresión algebraica, como los siguientes: a) Consideren la siguiente gráfica: Completen las descripciones de las siguientes situaciones de manera que correspondan a la gráfica anterior. Un taxi cobra 2 dólares por viaje más ______________ por cada kilómetro recorrido. 2 Un resorte de ____ cm de longitud alcanza una longitud de ____cm cuando se le pone una pesa de 2 gramos. Encuentren la expresión algebraica que corresponde a cada problema y digan si se trata de relaciones de proporcionalidad. _______ ¿Por qué? _______________ b) Inventen dos problemas que se puedan modelar con la siguiente gráfica: Observaciones posteriores 1. ¿Cuáles fueron los aspectos más exitosos de la sesión? _____________________________________________________________________ _____________________________________________________________________ _____________________________________________________________________ 2. ¿Cuáles cambios considera que deben hacerse para mejorar el plan de clase? _____________________________________________________________________ _____________________________________________________________________ _____________________________________________________________________ 3. Por favor, califique el plan de clase con respecto a su claridad y facilidad de uso para usted. Muy útil Útil Uso limitado 3 Pobre Ahora son diferentes Plan de clase (2/2) Escuela: _____________________________________________ Fecha: _______________ Profesor (a): _______________________________________________________________ Curso: Matemáticas 3 Secundaria Eje temático: MI Contenido: 9.1.4 Análisis de representaciones (gráficas, tabulares y algebraicas) que corresponden a una misma situación. Identificación de las que corresponden a una relación de proporcionalidad. Intenciones didácticas: Que los alumnos identifiquen que la misma tabla y representación algebraica puede modelar distintas situaciones. Consigna. En equipos, respondan lo que se pide a continuación. 1. Las tablas A y B representan dos situaciones distintas. x 2 3 4 10 Tabla A y 15.50 19.00 22.50 43.50 x 2 5 7 10 Tabla B y 15.50 38.75 54.25 77.50 Para cada una de las situaciones descritas a continuación, indiquen cuál es la tabla que corresponde: ( ) Un taxi cobra $8.50 por el “banderazo” (costo fijo al iniciar el viaje) más $3.50 por cada kilómetro recorrido. ( ) La compañía de teléfonos celulares Portátil cobra $7.75 por minuto en llamadas de larga distancia internacionales. ( ) La compañía de teléfonos celulares Estrella Móvil cobra por llamadas de larga distancia internacional: $15.50 por 2 minutos, $29.50 por 6 minutos, etcétera. ( ) Un atleta se está entrenado en montaña. Está corriendo a razón constante de 15.5 m por cada 2 s. ( ) Un automóvil tiene rendimiento de 46.5 km por cada 6 litros. 2. Encuentren las expresiones algebraicas que corresponden a las situaciones anteriores. ¿Cuántas expresiones algebraicas distintas encontraron?__________________ ¿Cuáles son? ________________________________________________________________ 3. Indiquen cuáles situaciones corresponden a relaciones de proporcionalidad y cuáles no. Argumenten sus respuestas. 4 Consideraciones previas: El énfasis de la sesión se da al carácter abstracto de las representaciones tabular y algebraica en términos de que a una misma expresión algebraica o tabla corresponden diversas situaciones. La tabla A corresponde a las situaciones del taxi y de la compañía de teléfonos Estrella Móvil, mientras que la tabla B corresponde a las otras tres situaciones. Una de las dificultades que pueden tener los alumnos es identificar cuál de las cantidades de cada situación corresponde a la variable x y cuál corresponde a la y. Puede intervenir ayudando a identificar, para cada situación, cuáles son las variables y cuáles son los valores que van tomando. Por ejemplo, es probable que algunos dividan el valor de y entre el valor de x tratando de obtener el valor unitario y se den cuenta que en la tabla A no corresponde, pues cuando x vale 3, el valor de y debiera ser 23.25 y, en este caso, es 19.00, lo cual lleva a pensar que seguramente existe un valor que se añade al valor de x para obtener y. Una vez relacionadas las tablas con las situaciones correspondientes, las representaciones algebraicas se pueden encontrar de varias maneras. Es importante considerar que quizás algunos alumnos no identifiquen inmediatamente que las situaciones que corresponden a la tabla A tendrán la misma representación algebraica (y = 3.50x + 8.50), y que pasa lo mismo para las situaciones que corresponden a la tabla B (y = 7.75x). Dé tiempo suficiente para que los alumnos exploren y propongan las representaciones que consideran adecuadas. Revísenlas en grupo. Las situaciones correspondientes a la tabla B son de proporcionalidad. Esto se puede verificar directamente de la tabla (al doble le corresponde el doble, etcétera), de la representación algebraica (y = mx) y de las condiciones mismas de los problemas (por ejemplo, cuando se da una razón constante: 2 s por cada 15.5 m) Si lo considera adecuado, pida que grafiquen las situaciones y comparen las gráficas correspondientes. Observaciones posteriores 1. ¿Cuáles fueron los aspectos más exitosos de la sesión? _____________________________________________________________________ _____________________________________________________________________ 2. ¿Cuáles cambios considera que deben hacerse para mejorar el plan de clase? _____________________________________________________________________ _____________________________________________________________________ 3. Por favor, califique el plan de clase con respecto a su claridad y facilidad de uso para usted. Muy útil Útil Uso limitado Pobre 14/15 5