Conversion de Numeros Complejos.

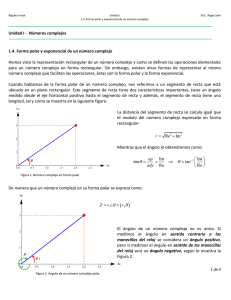
Yo eso de las Coordenadas Polares nunca lo pude entender,
por eso a mi nadie me seca de las Coordenadas Rectangulares
CONVERSIÓN DE NÚMEROS COMPLEJOS
DE FORMA RECTANGULAR A POLAR
Sea el número complejo 𝒂 + 𝒃𝒊, 𝒓 el segmento dirigido del origen del plano al punto Z
y 𝜽 el ángulo entre el eje R y la recta 𝒓 como se muestra.
i
Z
La longitud del segmento r será: √𝒂𝟐 + 𝒃𝟐
y el ángulo: 𝜽 = 𝑻𝒂𝒏−𝟏 (𝒃⁄𝒂)
𝒓
𝒃
𝜽
a
𝒃
R
Página 1 de 6
Por lo que para convertir un número complejo en la forma
Rectangular
a forma
Polar
𝒓 = √𝒂𝟐 + 𝒃𝟐
𝒂 + 𝒃𝒊
𝜽 = 𝑻𝒂𝒏−𝟏 (𝒃⁄𝒂)
Z=r∠θ
Nota: el ángulo 𝜽 puede expresarse en grados o en radianes. Si el
ángulo se expresa sin el signo de grados ( ° ), entonces se asumirá que
el ángulo está en radianes.
Ejercicio 1. Convierta losnúmeros complejos siguentes a forma polar:
𝒂) 𝒁𝟏 = 𝟐 + 𝟑𝒊,
𝒃) 𝒁𝟐 = 𝟐 − 𝟑𝒊
y
𝒄) 𝒁𝟑 = −𝟑 − 𝟐𝒊.
Soluciones:
𝒂) 𝒁𝟏 = 𝟐 + 𝟑𝒊,
Aplicando el Teotema de Pitágoras para 𝒂 = 𝟐 𝒚 𝒃 = 𝟑: 𝒓 = √𝟐𝟐 + 𝟑𝟐 = √𝟏𝟑 = 𝟑. 𝟔𝟏
𝒃
𝟑
y el ángulo (con 𝒂 = 𝟐 𝒚 𝒃 = 𝟑) será: 𝜽 = 𝑻𝒂𝒏−𝟏 ( ) = 𝑻𝒂𝒏−𝟏 ( ) = 𝟓𝟔. 𝟑𝟏°
𝒂
𝟐
Entonces 𝒁𝟏 en forma exponencial será: 𝒁𝟏 = 𝟑. 𝟔𝟏∠𝟓𝟔. 𝟑𝟏°
O también: 𝒁𝟏 = 𝟑. 𝟔𝟏𝑪𝒊𝑺(𝟓𝟔. 𝟑𝟏°)
𝒃) 𝒁𝟐 = 𝟐 − 𝟑𝒊
Como 𝒂 = 𝟐 𝒚 𝒃 = −𝟑: 𝒓 = √𝟐𝟐 + (−𝟑)𝟐 = √𝟏𝟑 = 𝟑. 𝟔𝟏
−𝟑
y el ángulo (con 𝒂 = 𝟐 𝒚 𝒃 = 𝟑) será: 𝜽 = 𝑻𝒂𝒏−𝟏 ( ) = −𝟓𝟔. 𝟑𝟏°; 𝜽 = −𝟓𝟔. 𝟑𝟏° +
𝟐
𝟑𝟔𝟎°
Entonces: 𝒁𝟐 = 𝟑. 𝟔𝟏𝑪𝒊𝑺(𝟑𝟎𝟑. 𝟔𝟗°) ó también: 𝒁𝟐 = 𝟑. 𝟔𝟏𝑪𝒊𝑺(𝟓. 𝟑𝟎)
Nota: el ángulo 𝜽 debe expresarse como el ángulo formado entre el Eje
X(+) y 𝒓. Los resultados de calcular el ángulo estarán dentro del rango:
−𝟗𝟎° < 𝜽 < 𝟗𝟎°. Por lo tanto, habrá que tomar en cuenta en qué cuadrante
del plano complejo está ubicado el número para determinar el valor de 𝜽
con respecto al eje X(+).
Página 2 de 6
 Resuelva 𝒁𝟑 = −𝟑 − 𝟐𝒊
DE FORMA POLAR A RECTANGULAR
Sea el número complejo Z en forma Polar: Z = r ∠ θ
i
Como 𝑺𝒆𝒏(𝜽) = (𝒃⁄𝒓)
Entonces: 𝒃 = 𝒓𝑺𝒆𝒏(𝜽)
así mismo, 𝑪𝒐𝒔(𝜽) = (𝒂⁄𝒓)
Por lo que: 𝒂 = 𝒓𝑪𝒐𝒔(𝜽)
Z
𝒓
𝒃
𝒃
𝜽
R
a
Entonces, para convertir un número complejo en la forma
Polar
Z=r∠θ
a forma
Rectangular
𝒂 = 𝒓𝑪𝒐𝒔(𝜽)
𝒃 = 𝒓𝑺𝒆𝒏(𝜽)
𝒂 + 𝒃𝒊
Nota: el ángulo 𝜽 puede estar expresado en grados o en radianes.
Ejercicio 2. Convierta losnúmeros complejos siguentes a forma Rectangular:
𝒂) 𝒁𝟏 = 𝟐 ∠ 𝟑𝟎°,
𝒃) 𝒁𝟐 = 𝟏𝟐 ∠ 𝟏𝟑𝟎°
y
𝒄) 𝒁𝟑 = 𝟏𝟓 𝒄𝒊𝒔 𝟑𝟑𝟎°.
Soluciones:
𝒂) 𝒁𝟏 = 𝟐 ∠ 𝟑𝟎°
Aplicando 𝒂 = 𝒓𝑪𝒐𝒔(𝜽) y 𝒃 = 𝒃 = 𝒓𝑺𝒆𝒏(𝜽) para 𝒓 = 𝟐 𝒚 𝜽 = 𝟑𝟎° obtenemos:
𝒂 = 𝟐𝑪𝒐𝒔(𝟑𝟎°) = 𝟏. 𝟕𝟑, y 𝒃 = 𝟐𝑺𝒆𝒏(𝟑𝟎°) = 𝟏. 𝟎𝟎, entonces, Z1 en forma
Rectangular es: Z1 = 1.73 + 1.00i
Página 3 de 6
 Resuelva los incisos b y c.
DE FORMA POLAR A EXPONENCIAL
Sea el número Complejo en forma Polar;
Z = r cis(θ)
Como el ángulo 𝜽 en un número complejo en forma Exponencial debe estar en
radianes, si está expresado en grados, será necesario convertirlo a radianes. Para
convertir el ángulo 𝜽 a radianes:
𝜽(𝒓𝒂𝒅) =
𝜽° × 𝝅
𝟏𝟖𝟎
Entonces, para convertir un número complejo en la forma
Polar
Z=r∠θ
a forma
𝜽𝒓𝒂𝒅 =
Exponencial
𝜽° × 𝝅
𝟏𝟖𝟎
𝒁 = 𝒓𝒆𝜽𝒊
Ejercicio 3. Convierta losnúmeros complejos siguentes a forma Rectangular:
𝒂) 𝒁𝟏 = 𝟐 ∠ 𝟑𝟎°,
𝒃) 𝒁𝟐 = 𝟏𝟐 ∠ 𝟐𝟑𝟎°
y
𝒄) 𝒁𝟑 = 𝟏𝟓 𝒄𝒊𝒔 𝟑𝟗𝟎°.
Soluciones:
𝒂) 𝒁𝟏 = 𝟐 ∠ 𝟑𝟎°
𝜽°×𝝅
Convertimos a 𝜽 en radianes: 𝜽𝒓𝒂𝒅 =
= 𝟑𝟎° × 𝝅 ÷ 𝟏𝟖𝟎 = 𝟎. 𝟓𝟐𝒓𝒂𝒅
𝟏𝟖𝟎
Entonces: 𝒁𝟏 = 𝟐𝒆𝟎.𝟓𝟐𝒊
Tanbién puede representarse como:
𝒁𝟏 = 𝟐𝒆(𝟏⁄𝟔)𝒊
 Resuelva los incisos b y c.
 ¿Qué relación nota entre en el resultado del inciso c) con los dos anteriores
 ¿a qué se debe?
Página 4 de 6
DE FORMA EXPONENCIAL A POLAR
Sea el número Complejo en forma Exponencial;
𝒁 = 𝒓𝒆𝜽𝒊
Como el ángulo 𝜽 en un número complejo en forma Exponencial está en radianes,
pudiera ser necesario convertirlo a grados. Para convertir el ángulo 𝜽 a grados:
𝜽° =
𝜽𝒓𝒂𝒅 × 𝟏𝟖𝟎°
𝝅
Entonces, para convertir un número complejo en la forma
Exponencial
a forma
Polar
𝜽𝒓𝒂𝒅 × 𝟏𝟖𝟎°
Z=r∠θ
𝜽° =
𝒁 = 𝒓𝒆
𝝅
Nota: Recuerde que el ángulo 𝜽 puede expresarse en grados o en radianes,
𝜽𝒊
pero, lo expresaremos en grados,debido a que generalmente es en esta forma como
expresamos los ángulos.
Ejercicio 4. Convierta losnúmeros complejos siguentes a forma Polar:
𝒂) 𝒁𝟏 = 𝟐 𝒆𝟐.𝟓𝒊 ,
𝒃) 𝒁𝟐 = 𝟓 𝒆𝟏.𝟓𝝅𝒋
y
𝒄) 𝒁𝟑 = 𝟓 𝒆𝟕.𝟓𝒋 .
Soluciones:
𝒂) 𝒁𝟏 = 𝟐 𝒆𝟐.𝟓𝒊
Convertimos 𝜽 = 𝟐. 𝟓 (𝒓𝒂𝒅) a grados: 𝜽° =
𝟐.𝟓𝒓𝒂𝒅 ×𝟏𝟖𝟎°
𝝅
= 𝟏𝟒𝟑. 𝟐𝟒°
Como 𝒓 = 𝟐, entonces: 𝒁𝟏 = 𝟐𝑪𝒊𝑺(𝟏𝟒𝟑. 𝟐𝟒°)
Resuelva los incisos b y c
No existe la forma de convertir números complejos en forma Rectangular a
exponencial; ni en forma exponencial a rectangular de manera directa. Por
lo tanto, será necesario convertirlos primero a forma polar y después
pasarlos a forma Rectangular o Exponencial, según el caso.
Página 5 de 6
Ejercicio 5. Convierta losnúmeros complejos siguentes a forma Exponencial:
𝒂) 𝒁𝟏 = 𝟐 + 𝟑𝒊,
𝒃) 𝒁𝟐 = 𝟐 − 𝟑𝒊
y
𝒄) 𝒁𝟑 = −𝟑 − 𝟐𝒊.
Ejercicio 6. Convierta losnúmeros complejos siguentes a forma Rectangular:
𝒂) 𝒁𝟏 = 𝟐 𝒆𝟐.𝟓𝒊 ,
𝒃) 𝒁𝟐 = 𝟓 𝒆𝟏.𝟓𝝅𝒋
y
𝒄) 𝒁𝟑 = 𝟓 𝒆𝟕.𝟓𝒋 .
Página 6 de 6