Considérese un cilindro horizontal de 15 cm de diámetro y 75 cm de
Anuncio

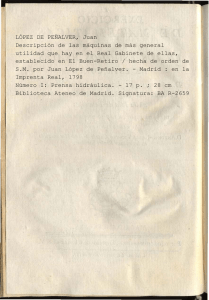
2.19. a) b) c) d) e) Considérese un cilindro horizontal de 15 cm de diámetro y 75 cm de longitud, cerrado por ambos extremos, con un émbolo cilíndrico de 2 kg de acero, cuyo centro está inicialmente a ¼ de la longitud del cilindro, separando dos masas de aire. La presión y la temperatura iniciales del conjunto son las del ambiente, que está a 20 ºC y 94 kPa. En una primera etapa se fuerza el desplazamiento del émbolo, lentamente, hasta la posición central del cilindro, y a partir de ahí se suelta. Se pide: Estimar el efecto del espesor del émbolo y calcular el trabajo necesario para desplazar el émbolo. Flujos de energía en el proceso anterior, para cada masa de aire. Estado de equilibrio mecánico tras la suelta (antes del atemperamiento). Flujos de energía en el proceso anterior, para cada masa de aire. Calor intercambiado con el ambiente y generación de entropía en el proceso global. Solución Fig. 1. Configuración y notación. a) Estimar el efecto del espesor del émbolo y calcular el trabajo necesario para desplazar el émbolo. El espesor del émbolo, , se deduce de su masa (2 kg) y la densidad del acero (7800 kg/m 3): =mE/(EA)=2/(7800·0,0177)=14,5 mm, siendo A=D2/4=0,152/4=0,0177 m2 el área de la sección recta. Aunque se duplicase su efecto por incidir en ambos volúmenes de gas, no sería más que 2/L=2·0,0145/0,75=4%, así que lo despreciamos (las incertidumbres en el modelo de fricción y en las aproximaciones isotermas y adiabáticas pueden ser mayores). Las masas de aire encerrado se obtienen de m=pV/(RT): mA=p0(1/4)AL/(RT0)= 94000·(1/4)·0,0177·0,75/(287·293)=0,0037 kg (unos 4 g), y mB=3mA=0,011 kg. El trabajo necesario será la integral de la fuerza por el desplazamiento que hay que hacer al empujar el émbolo (con un dispositivo no descrito, e.g. un imán exterior): WE=(pBpA)Adx, que al ser el proceso isotermo, WE=(mBRT0/(Lx)mART0/x))dx=mBRT0ln((Lx2)/(Lx1))mART0ln(x2/x1)= 0,011·287·293·ln(2/3)0,0037·287·293·ln(2)=163 J, i.e. unos 160 J. En el equilibro final, los volúmenes son iguales, las temperaturas también, pero las presiones serán proporcionales a las masas; de p=mRT/V obtenemos: pA2=47 kPa y pB2=140 kPa. b) Flujos de energía en el proceso anterior, para cada masa de aire. Al ser todo el proceso isotermo, con el modelo de gas ideal E=0=W+Q. Para el A, QA=WA=pAAdx=mART0ln(x2/x1)=216 J (unos 220 J). Para el B, QB=WB=pBAdx=mBRT0ln((Lx2)/(Lx1))=379 J (unos 380 J). Nótese que el calor total, QA=QA=216379=163 J, se compensa con el trabajo del apartado anterior. c) Estado de equilibrio mecánico tras la suelta (antes del atemperamiento). Esta evolución puede suponerse isentrópica para cada gas, i.e. pV=cte., porque no da tiempo a la transmisión de calor, y la disipación tendrá lugar en la fricción émbolo-cilindro y no en los gases. De la igualdad de presiones en el equilibrio mecánico, pA2(x2/x3)=pB2((Lx2)/(Lx3)), con la única incógnita x3 obtenemos, x3=0,235 m (unos 23 cm). En ese momento, pA=pB=90,4 kPa, TA=353 K y TB=258 K. d) Flujos de energía en el proceso anterior, para cada masa de aire. La evolución de 2 a 3 es rápida (adiabática), por lo que el balance energético de cada gas, E=W+Q, queda W=E. Para el A, WA=mAcv(T3T2)=mA(cpR)T0(T3/T2)=mA(cpR)T0((x2/x3))= 0,0037·(1000-287)·293·((0,375/0,235)0,41)=160 J. Para el B, WB=mBcv(T3T2)= mB(cpR)T0(((Lx2)/(Lx3)))=0,011·(1000-287)·293·((0,375/(0,750,235))0,41)=278 J (unos 280 J). La diferencia de módulos será el trabajo disipado por fricción, =|WB||WA|=278160=128 J. e) Calor intercambiado con el ambiente y generación de entropía en el proceso global. De 3 a 4 todo se atemperará, y como el proceso global es cíclico (el sistema vuelve a su estado inicial), 0=E=0=W+Q=Q12+Q23+Q34+W12+W23+W34=Q12+Q34+W12 ya que para el conjunto W34=0, luego ha de ser también Q34=0. Para el sistema conjunto, A+B+C+E (gas A más gas B más cilindro más émbolo), en el proceso global, 1-2-3-4, es cíclico, y por tanto Q=W=163 J (unos 160 J). Y como el universo (i.e. conjunto más ambiente) es un sistema aislado, =S+Samb=Samb=Qamb/Tamb=Q/Tamb=163/293=0,56 J/K.