Mediatriz: La mediatriz de un segmento es la recta
Anuncio

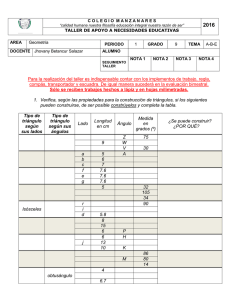
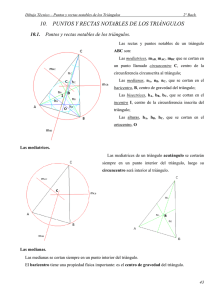
Mediatriz: La mediatriz de un segmento es la recta perpendicular a dicho segmento trazada por su punto medio. Bisectriz: La bisectriz de un ángulo es la recta que lo divide en dos partes iguales. Es el lugar geométrico de los puntos del plano que equidistan (están a la misma distancia) de las semirrectas de un ángulo. Mediana: la línea que une cualquier vértice de un triangulo con el centro del lado opuesto. Altura: el alto dimensional (o altura) es una dimensión de un objeto plano o volumen, normalmente vertical. Circuncentro: es el punto en que se cortan las tres mediatrices de un triángulo y es el centro de la circunferencia circunscrita. Los vértices de un triángulo, como extremos de cada lado, se encuentran a la misma distancia de los puntos de sus mediatrices, luego el punto donde estas se cortan, será equidistante de los tres vértices: el circuncentro. Baricentro: el baricentro o centroide de una superficie contenida en una figura geométrica plana, es un punto tal, que cualquier recta que pasa por él, divide a dicha superficie en dos partes de igual momento respecto a dicha recta. Ortocentro: punto donde se cortan las tres alturas de un triángulo. Este no es un hecho trivial, pues tres rectas cualquiera, tomadas a pares, podrían intersectarse en tres puntos diferentes, pero en el caso de las alturas de un triángulo dado, puede demostrarse que se intersectan en un solo punto, es decir, en el ortocentro. Incentro: se denomina al centro de la circunferencia inscrita en un triángulo, y equidista de sus tres lados. Es el punto donde se cortan las bisectrices de los ángulos interiores de dicho triángulo. El incentro puede hallarse intersectando sólo dos bisectrices, pues la tercera pasará siempre por este punto. Es el centro de la mayor circunferencia posible trazada dentro del triangulo. Teorema de Euler: La recta de Euler de un triángulo es aquella que contiene al ortocentro, al circuncentro y al baricentro del mismo. Se llama así, en honor al matemático suizo Leonhard Euler quien descubrió este hecho a mediados del siglo XVIII.