Apellidos: Nombre: Sección:

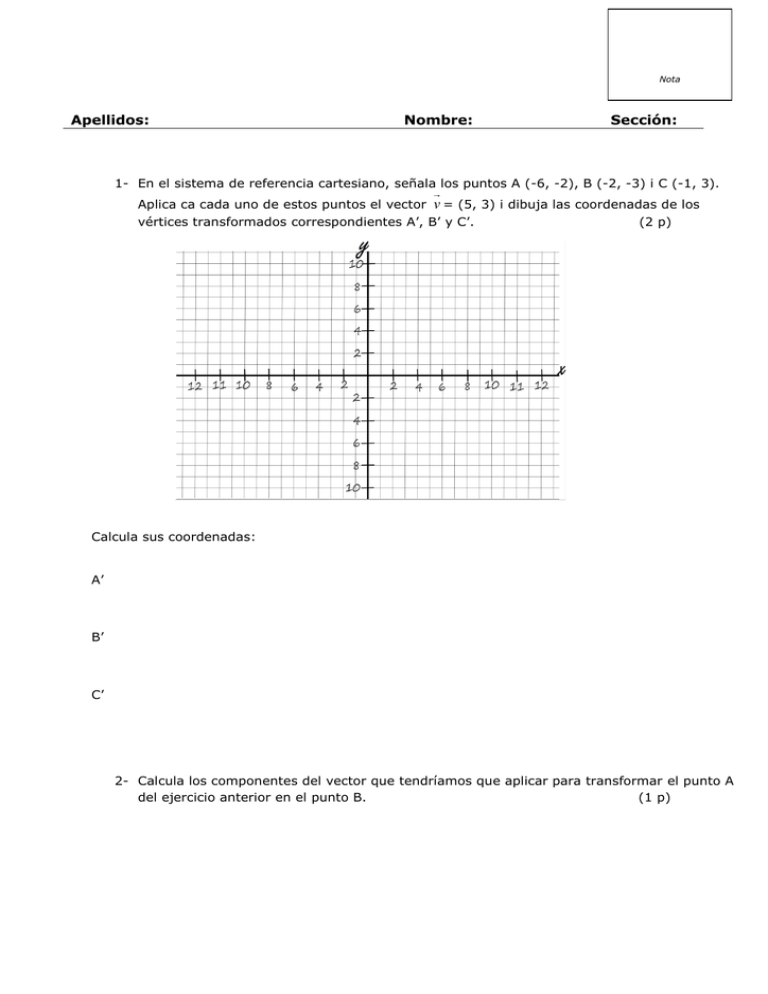
Nota
Apellidos:
Nombre:
Sección:
1- En el sistema de referencia cartesiano, señala los puntos A (-6, -2), B (-2, -3) i C (-1, 3).
Aplica ca cada uno de estos puntos el vector
v = (5, 3) i dibuja las coordenadas de los
vértices transformados correspondientes A’, B’ y C’.
(2 p)
Calcula sus coordenadas:
A’
B’
C’
2- Calcula los componentes del vector que tendríamos que aplicar para transformar el punto A
del ejercicio anterior en el punto B.
(1 p)
3- Encuentra las coordenadas de los puntos homólogos del punto P (-2, 5) mediante cada uno
de los giros siguientes, todos ellos con el centro al origen de las coordenadas:
(2 p)
a) 90º
b) 270º
c) -180º
d) -270º
4- Dado un cuadrilátero de vértices A (1, -2), B (3, -4), C (5, 0) y D (7, -1).
(3 p)
a) Determina las coordenadas de los vértices A’ B’ C’ D’, simétrico del cuadrilátero ABCD
respecto al eje de las abscisas.
b) Determina las coordenadas de los vértices A’ B’ C’ D’, simétrico del cuadrilátero ABCD
respecto al eje de las ordenadas.
c) Dibuja el cuadrilátero resultante al haber aplicado las simetrías de apartado a y b.
5- Tenemos un triángulo equilátero de 4 cm de lado al cual le aplicamos una homotecia de
k=2.
(2 p)
a) Determina cuanto mesurarán los lados homotéticos de la nueva figura.
b) Calcula cuanto valdrá el perímetro del triángulo homotético.
c) Calcula cuanto valdrá la área del polígono homotético.