Vectores en el plano - Traslaciones - Giros - Simetr as
Anuncio

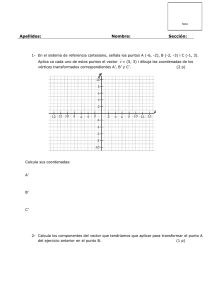
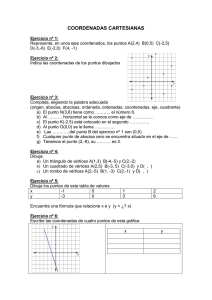
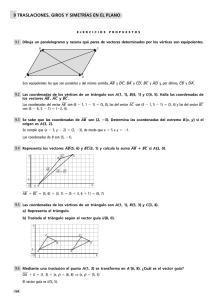
IES PADRE FEIJOO MATEMÁTICAS 3º ESO VECTORES EN EL PLANO – TRASLACIONES – GIROS – SIMETRÍAS 1.- Calcula las componentes del vector AB siendo A(6,1) y B(3,–2). 2.- Dado el vector AB , calcula sus componentes y su módulo siendo A(3,0) y B(4,2). 3.- Dados los puntos A(4,4) y B(3,5), ¿cuáles son las componentes del vector AB ? ¿Y las del vector BA ? 4.- El vector CD tiene como componentes (3,–4) y el punto D tiene como coordenadas (–2,1). ¿Cuáles son las coordenadas del punto C? 5.- Dados los vectores u (3, 7 ) , v ( −5, 6) y w ( −2, − 3) : a) Calcula las componentes de los siguientes vectores: u +v v + w u + v + w b) Representa gráficamente la suma de los vectores anteriores. 6.- Una traslación transforma el punto A(2,5) en el B(3,4). Calcula las coordenadas del vector libre que define la traslación y halla su módulo. 7.- Considera el triángulo de vértices A(–5,–3), B(0,–4) y C(–1,1). Realiza una traslación del triángulo según el vector de traslación u (5, 3) . Representa ambos triángulos. 8.- Representa un cuadrilátero de vértices A(–2,–2), B(2,–1), C(2,3) y D(–4,2). Traslada dicho cuadrilátero según el vector de traslación u ( 2, 1) . Representa el nuevo cuadrilátero. 9.- Calcula las coordenadas del cuadrado que resulta de trasladar el cuadrado de vértices A(0,0), B(1,0), C(1,1) y D(0,1) según el vector u (−3, 2) . Dibuja ambos cuadrados. 10.- Transforma el triángulo de vértices A(1,4), B(–2,4) y C(–1,2) mediante un giro de 180º con centro en O(3,2). 11.- Dado el triángulo de vértices A(–3,2), B(–2,–1) y C(0,0). Representa el triángulo homólogo al aplicarle un giro de –90º con centro el origen de coordenadas. 12.- Calcula las coordenadas del transformado del triángulo de vértices A(–1,–3), B(2,–1) y C(3,3) mediante un giro de 90º con centro en O(4,1). 13.- Dibuja un cuadrado que tiene por vértices A(5,4), B(–1,4), C(–1,–2) y D(5,–2). Aplícale un giro de 90º cuyo centro sea el origen de coordenadas y determina las coordenadas de los vértices del nuevo cuadrado. 14.- Consideramos el triángulo de vértices A(0,0), B(3,1) y C(2,5). Calcula las coordenadas de su simétrico respecto del eje de abscisas, del eje de ordenadas y del origen de coordenadas. Dibuja la figura resultante en cada caso. 15.- Consideramos el cuadrilátero de coordenadas A(–2,–1), B(3,2), C(2,4) y D(1,2). Calcula su simétrico respecto del origen de coordenadas y dibuja ambas figuras. 16.- Dado el triángulo de vértices A(–3,–1), B(1,3) y C(–2,4). Calcula las coordenadas de los vértices del triángulo obtenido al aplicarle al triángulo anterior una simetría respecto: a) Del eje de abscisas. b) Del eje de ordenadas c) Del origen de coordenadas 17.- Calcula el simétrico respecto del origen de coordenadas del cuadrilátero de vértices A(2,1), B(6,2), C(2,5) y D(1,3). 18.- Dibuja y señala todos los ejes de simetría de un triángulo equilátero, un cuadrado, un pentágono regular y un hexágono regular. ¿Cuántos ejes de simetría tienen cada uno de los polígonos regulares anteriores? 19.- Dibuja y señala todos los ejes de simetría de un triángulo isósceles, un rectángulo, un rombo y un trapecio isósceles. ¿Cuántos ejes de simetría tienen cada uno de los polígonos anteriores? 20.- Sea la circunferencia con centro en O(3,2) y de radio 2 que pasa por los puntos A(3,0), B(3,5), C(5,2) y D(1,2). Dibuja la circunferencia simétrica a la dada respecto del eje de ordenadas (calcula los homólogos de los puntos dados).