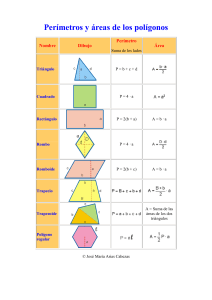
Poliedros Control B
Anuncio

Poliedros Control B Ejercicio nº 1.Escribe el nombre de cada uno de los elementos de este poliedro: Solución: Ejercicio nº 2.- ¿Cuáles de las siguientes figuras son poliedros? ¿Por qué? Solución: Son poliedros A y B porque son cuerpos geométricos limitados por polígonos. Ejercicio nº 3.- Indica qué tipo de poliedro es cada uno de estos: Solución: A Prisma recto B Tronco de pirámide C Pirámide pentagonal Ejercicio nº 4.- Describe el siguiente poliedro y clasifícalo atendiendo a sus características: Solución: 2 bases triangulares. 3 caras rectangulares. Prisma recto. Prisma triangular. Ejercicio nº 5.Las bases de un prisma recto son triángulos rectángulos cuyos catetos miden 9 cm y 12 cm. La altura del prisma es 10 cm. Calcula el área total. NOTA: Recuerda que para calcular la hipotenusa del triángulo rectángulo has de utilizar el teorema de Pitágoras. Solución: x 12 2 9 2 15 cm b h 12 9 54 cm2 2 2 ABASE P a 36 10 180 cm2 2 2 ATOTAL 180 2 54 288 cm2 ALATERAL ATOTAL ALATERAL 2 ABASE Ejercicio nº 6.- Dibuja esquemáticamente el desarrollo de esta pirámide y calcula su área total sabiendo que todas sus caras son triángulos equiláteros de 8 cm de lado. NOTA: Recuerda que para calcular la apotema de la pirámide (a), has de utilizar el teorema de Pitágoras. Solución: a 82 42 ABASE ALATERAL h 8 2 4 2 6, 9 cm 8 6, 9 27, 6 cm2 2 24 6, 9 82, 8 cm2 2 ATOTAL 27, 6 82, 8 110, 4 cm2 Ejercicio nº 7.- Calcula su área lateral con las dimensiones del dibujo: Solución: ALATERAL 6 Ejercicio nº 8.este ortoedro: Solución: 52 12 21 4 032 cm2 2 Calcula la diagonal de d a2 b2 c 2 d 30 2 5 2 6 2 d 31 cm Ejercicio nº 9.- Calcula la altura de una pirámide hexagonal regular de 40 cm de arista lateral y cuya base tiene 29 cm de lado. Solución: a 402 292 27,5 cm a 27,5 cm Ejercicio nº 10.- Calcula el área total de esta pirámide regular cuya base es un cuadrado de 12 cm de lado y su altura es de 8 cm. Solución: a 8 2 6 2 10 cm ABASE 12 144 cm 12 10 48 10 ALATERAL 4 240 cm2 2 2 ATOTAL A BASE A LATERAL 2 2 A TOTAL 144 240 384 cm2 Ejercicio nº 11.- ¿Cuál es el precio de un cajón de embalaje de 60 cm 40 cm 50 cm si la 2 madera cuesta a razón de 18 euros/m ? Solución: ABASE 06 · 04 024 cm 2 ALATERAL PBASE · a 2 · 05 1 m 2 ATOTAL 2ABASE ALATERAL 048 1 148 m 2 148 · 18 2664 euros es el precio