GUÍA DE UNIDAD Nº 3: AREAS Y VOLÚMENES
Anuncio

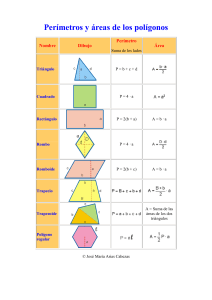
LICEO TECNICO CLELIA CLAVEL DINATOR SECTOR: MATEMÁTICA DOCENTE: SIXTA POSTIGOMORENO NIVEL: CUARTO MEDIO GUÍA DE UNIDAD Nº 3: AREAS Y VOLÚMENES APRENDIZAJE ESPERADO: 1) Calcula áreas y volúmenes de cuerpos geométricos 2) Resuelve problemas sobre áreas y volúmenes de cuerpos geométricos DESTREZAS: 1) Calcular; 2) Resolver CONTENIDO ASOCIADO: ÁREAS Y VOLÚMENES INSTRUCCIONES GENERALES: 1º Cada alumna desarrolla los ejercicios en su cuaderno 2º Compara sus resultados con las compañeras de su grupo 3º Cada tutora o alumna encargada de fila revisa el trabajo de las compañeras a su cargo 4º Se evaluará el aprendizaje de cada ítem de la guía con una breve interrogación UNIDAD 3: ÁREA Y VOLÚMENES I C I L I N D R O Atotal = 2πr(h + r), donde h es la altura del cilindro y r es el radio de la base. Ejemplo: Si h = 8 cm y r = 9 cm, π = 3,14 Atotal = 2 3,14 9 (8 +9) = 960,84 cm2 VOLUMEN: V = πr2 h Ejemplo: r = 5 m; h = 12 m V = 3,14 52 12 = 942 m3 EJERCICIOS 1) ¿Cuál es Atotal y el volumen de un tubo de acero con forma cilíndrica si su radio basal mide 5 cm y su largo 2 m? ¿Cuántos cm3 de pintura se necesitan para pintar estos tubos? (1 litro de pintura = 1000 cm3 rinde aproximadamente 3 m2) 2) Se construyó un pozo de de altura120 cm. Y diámetro de 1 metro ¿Cuál es su volumen? 3) Las bebidas de lata, en general tienen el mismo volumen (350 cm3) y tienen forma cilíndrica. ¿Cuál debería ser el diámetro de la base de cada lata si ahora todas deben tener una altura de 5 cm? 4) El volumen de un cubo es 360π m3. Calcula la medida de su radio basal y el área total si tiene una altura de 10 m. 5) Un envase pintura de forma cilíndrica 20 cm de altura y su radio basal mide 8 cm. ¿Cuántos litros de pintura contiene? 6) Los tubos de una conducción de gas tiene 8 cm. de diámetro. Para pintarlos se necesita 1 litro de pintura por cada 2 m2 ¿Cuántos litros se necesitan para pintar una conducción de 250 m de longitud? 7) ¿Cuántos centímetros de papel se necesitan para una etiqueta de una lata cilíndrica de 10 cm. de altura y base circular de 6 cm. de diámetro? 8) Las dimensiones de una boya cilíndrica son r = 2 m y h = 2 m ¿Cuál es el Atotal y el volumen de la boya? II Generatriz: C O N O g2 = r2 + h2 Ejemplo: Si r = 5 cm y h = 12 cm, 2 2 2 R E C T O EJERCICIOS 1) Calcula la altura, el ALateral, Atotal y el volumen de un cono recto cuya generatriz mide 20 cm. y su radio basal mide 15 cm. 2) En una planta de salitre almacenan el mineral formando cerros con forma similar a un cono de dimensiones: 40 cm. de radio y 10 m de altura. Si el salitre acumulado debe ser transportado en un camión con capacidad de carga de 300 m3 ¿Cuántos viajes debe realizar el camión? 3) ¿Cuál es el ALateral y el volumen de un cono recto cuya región basal tiene un área de 25π cm2 y su altura mide 12 cm? 4) Las alturas de dos conos de igual base miden 14 y 6 cm respectivamente. Halla el volumen del cono mayor sabiendo que el del menor es de 81 cm35) La generatriz de un cono recto mide 13 cm. y la altura 12 cm. Para que su volumen sea 100π cm3 ¿Cuánto debe medir su radio basal? 6) C a l c u l a e l á r e a l a t er a l , t o t a l y e l vo l u m e n d e u n c o n o c u ya a l t u r a m i d e 4 cm y el radio de la base es de 3 cm. 7) P a r a u n a f i e s t a, L uís h a h e c h o 1 0 g o r r o s d e f or m a c ó n i ca c o n c ar t ón. ¿ C u á n t o c a r t ó n h a br á u t i l i za d o s i l a s d i m e n s i o n e s d e l g or r o s o n 1 5 c m d e r a d i o y 2 5 cm d e g en e r a t r i z? III E S F Área de la esfera = 4πr2 Ejemplo: Si r = 5 m y π = 3 Volumen: A E R A = 4π 52 = 300 m2 4 3 πr 3 Ejemplo: Si r = 8 cm y π = 3 V = 4 3 83 = 3 EJERCICIOS 1) 2) 3) 4) 5) El área de una esfera es 286π cm2. Calcula su radio y su volumen Halla el área m2 de una esfera de 1 m de radio. Calcula el área de m2 de una esfera de 0,8 m de diámetro Calcula en km2 el área de la superficie terrestre, si el radio de la Tierra es 6370 km. Calcula el área y el volumen de una esfera de 7,5 cm de radio IV C U B O a Diagonal del cubo: D = a 3 Ejemplo: Si a = 2 12 cm D = 2 12 Atotal = 6a2 3 =2 36 = 12 cm Ejemplo: Si a = 12 mm Atotal = 6 122 = 864 mm2 Volumen: V = a3 Ejemplo Si a = 5 Hm V = 53 = 125 Hm3 EJERCICIOS 1) La medida de la diagonal de un cubo es 35 3 . ¿Cuánto mide su arista y cuál es su volumen? 2) El volumen de un cubo es 729 m3. ¿Cuánto mide su arista y el Atotal? 3 V PRISMA RECTO DE BASE RECTANGULAR: Abasal = 2ab Ejemplo: Si a = 8 cm y b = 10 cm Abasal = 2 8 10 = 160 cm2 Alateral = 2ac + 2bc Ejemplo: Si a = 5 m; b = 7 m y c = 11 m Alateral = 2 8 11 + 2 7 11 = 330 m2 Atotal = Abasal + Alateral Ejemplo: Si a = 5 mm b = 6 mm c = 9 mm Atotal = 2 5 6 + 2 5 9 + 2 6 9 = 258 mm2 Volumen: V = a b c Ejemplo Si a = 7 m b = 13 m c = 15 m V = 7 13 15 = 1-365 m3 EJERCICIOS: 1) 2) Calcula el volumen, en centímetros cúbicos, de una habitación que tiene 5 m de largo, 40 dm de ancho y 2500 mm de alto. Una piscina tiene 8 m de largo, 6 m de ancho y 1.5 m de profundidad. Se pinta la piscina a razón de 6 € el metro cuadrado . ¿Cuánto costará pintarla? ¿Cuántos litros de agua se necesitan para llenarla? DESARROLLO: Como la piscina corresponde rectangular sin tapa, el área sería: a un prisma recto A = 8 6 + 2 8 1,5 + 2 6 1,5 = 90 m2 Costo de pintura: 90 6€ = 5 4 0 € V = 8 6 1,5 = 72 m3, 3) 4) 72 1.000 = 72.000 litros Una piscina tiene 10 m de largo, 5 m de ancho y 2 m de profundidad. Se pinta la piscina a razón de 6 € el metro cuadrado. ¿Cuánto costará pintarla? ¿Cuántos litros de agua se necesitan para llenarla? Calcula la altura de un prisma que tiene 12 dm2 de área y contiene 48.000 litros de aceite. VI PIRAMIDE DE BASE RECTANGULAR: Abasal = ab Ejemplo: Si a = 8 cm y b = 10 cm Abasal = 8 10 = 80 cm2 2( a b ) A p Alateral = 2 Ejemplo: Si a = 7 cm b= 5cm Ap = 15 cm 2(7 5) 15 2 Alateral = b a Atotal = Abasal + Alateral Volumen: V = Ejemplo: 80 + 180 = 260 m2 abh 3 Ejemplo Si a = 5 dm V= = 180 cm2 b = 9 dm h = 12 dm abh = 5 9 12 = 180 dm3 3) Calcula el área lateral, total y el volumen de una pirámide cuadrangular de 10 cm de arista básica y 12 cm de altura. DESARROLLO: (Ap)2 = 52 + 122 = 169 Ap = 13 cm Pbase = 4 10 = 40 cm (P = Perímetro) 40 13 = 260 cm2 2 Atotal = 260 + 102 = 360 cm2 Alateral = V= 1000 12 = 4.000 cm3 3 4) Calcula el área lateral, total y el volumen de una pirámide cuadrangular de 15 cm de arista básica y 24 cm de altura. CALCULO DE AREAS Y VOLUMENES CON COMBINACIÓN DE CUERPOS GEOMÉTRICOS Y EJERCICIOS RESUELTOS 1) En un almacén de 5 m de largo, 3 m de ancho y 2 m de alto queremos almacenar cajas de dimensiones 10 dm de largo, 6 dm de ancho y 4 dm de alto. ¿Cuántas cajas se pueden almacenar? DESARROLLO: 1 m = 10 dm Volumen Almacén: V = 50 30 20 = 30000 dm3 Volumen Caja: V = 10 6 4 = 240 dm3 Cantidad de cajas: 30.000 : 240 = 125 cajas. 2) En un almacén de 6 m de largo, 4 m de ancho y 3 m de alto queremos almacenar cajas cuyas dimensiones son 15 cm de largo, 8 cm de ancho y 12 cm de alto. ¿Cuántas cajas se pueden almacenar? 3) En una bodega de 9 m de largo, 7 m de ancho y 5 m de alto queremos almacenar cajas cuyas dimensiones son 20 cm de largo, 18 cm de ancho y 25 cm de alto. ¿Cuántas cajas se pueden almacenar? 4) Calcula la cantidad de hojalata que se necesitará para hacer 10 botes de forma cilíndrica de 10 cm de diámetro y 20 cm. de altura. DESARROLLO: 785.398 10 = 7.853.980 cm2 5) Calcula la cantidad de hojalata que se necesitará para hacer 20 botes de forma cilíndrica de 12 cm de diámetro y 40 cm. de altura 6) Calcula la cantidad de hojalata que se necesitará para hacer 10 botes de forma cilíndrica de 24 cm de diámetro y 10 cm. de altura 7) Una empresa necesita 300 envases de cartón de forma cilíndrica, de 28 cm de diámetro y 50 cm. de altura. ¿Cuántos metros de cartón se necesita comprar para confeccionarlos? 8) Una empresa necesita 1.000 envases de cartón de forma cilíndrica, de 20 cm de diámetro y 30 cm. de altura. ¿Cuántos metros de cartón se necesita comprar para confeccionarlos? 10) Un cilindro tiene por altura la misma longitud que la circunferencia de la base. Y la altura mide 157 cm. Calcula el área total y el volumen. Considera π = 3,14 11) Un cilindro tiene por altura la misma longitud que la circunferencia de la base. Y la altura mide 157 cm. Calcula el área total y el volumen. Considera π = 3,14 12) En una probeta de 10 cm de radio, se echan cuatro cubitos de hielo de 4 cm de arista. ¿A qué altura llegará el agua cuando se derritan? 13) En una probeta de 6 cm de radio, se echan cuatro cubitos de hielo de 4 cm de arista- ¿A qué altura llegará el agua cuando se derritan? DESARROLLO: 14) La cúpula de una catedral tiene forma semiesférica, de radio 50 m. Si restaurarla tiene un costo de 300 € el m2 ¿A cuánto ascenderá el presupuesto de la restauración? Considera π= 3,1415 DESARROLLO: Á r e a S e m i e sf e r a: A S E = 2 π 502 = 15.707,96 m2 C o s t o : 15.707,96 300 € = 4. 7 1 2 . 3 8 8 € 15) La cúpula de una catedral tiene forma semiesférica, de radio 40 m. Si restaurarla tiene un costo de 250 € e l m 2 ¿A cuánto ascenderá el presupuesto de la restauración? Considera π= 3,141592 16) La cúpula de una catedral tiene forma semiesférica, de radio 60 m. Si restaurarla tiene un costo de 180 € e l m 2 ¿A cuánto ascenderá el presupuesto de la restauración? Considera π= 3,14 17) ¿Cuántas losetas cuadradas de 20 cm de lado se necesitan para recubrir las caras de una piscina de 10 m de largo por 6 m de ancho y 3 m de profundidad? DESARROLLO: Apiscina = 10 6 + 2 10 3 + 2 6 3 = 156 m2 Aloseta = 20 20 = 400 cm2 : 10.000 = 0,04 m2 Cantidad de losetas: 156 : 0,04 = 3900 18) ¿Cuántas losetas cuadradas de 30 cm de lado se necesitan para recubrir las caras de una piscina de 12 m de largo por 8 m de ancho y 4 m de profundidad? 19) ¿Cuántas losetas cuadradas de 25 cm de lado se necesitan para recubrir las caras de una piscina de 14 m de largo por 6 m de ancho y 5 m de profundidad? 20) ¿Cuántas losetas rectangulares de 20 cm de largo y 12 cm de ancho se necesitan para recubrir las caras de una piscina de 20 m de largo por 8 m de ancho y 6 m de profundidad? 21) Un recipiente cilíndrico de 5 cm. de radio y 10 cm. de altura se llena de agua. Si la masa del recipiente lleno es 2 Kg ¿Cuál es la masa del recipiente? (π = 3 , 1 4 ) DESARROLLO: V = π 102 5 = 1.570 cm3 = 1,57 dm3 1,57 dm3 = 1, 57 Kg Masa del recipiente: 2 - 1,57 = 0,43 Kg 25) Para una fiesta, Luis confeccionará 10 gorros de forma cónica con cartón. ¿Cuánto cartón necesitará si las dimensiones del gorro son 15 cm. de radio y 25 cm. de generatriz? ( DESARROLLO A = π 15 25 = 1178,097 cm2 por un gorro 10 1178,097 = 11.780,97 cm2 26) Un cubo de 20 cm. de arista está lleno de agua. ¿Cabría esta agua en una esfera de 20 cm. de radio? 27) Calcula el área lateral, área total y el volumen de un cono cuya generatriz mide 13 cm. y el radio de la base mide 5 cm. 28) Calcula el área lateral, el área total y el volumen de un cono cuya altura mide 4 cm. y el radio de la base mide 3 cm. 29) Calcula el área y el volumen de una esfera inscrita en un cilindro de 2 m de altura. 30) Calcular el volumen de una semiesfera de 10 cm. de radio. 31) La gran pirámide de Giza es la única que perdura de las siete maravillas del mundo antiguo. Actualmente tiene una altura de 137 m. y la base es un cuadrado de 230 m de lado. ¿Cuál es aproximadamente, su volumen?

![• (1JJ [b [M]](http://s2.studylib.es/store/data/001660247_1-1b1ec3f2af6ce5b36615782edea2e40e-300x300.png)



