4º Equilibrio Bayesiano de Nash
Anuncio
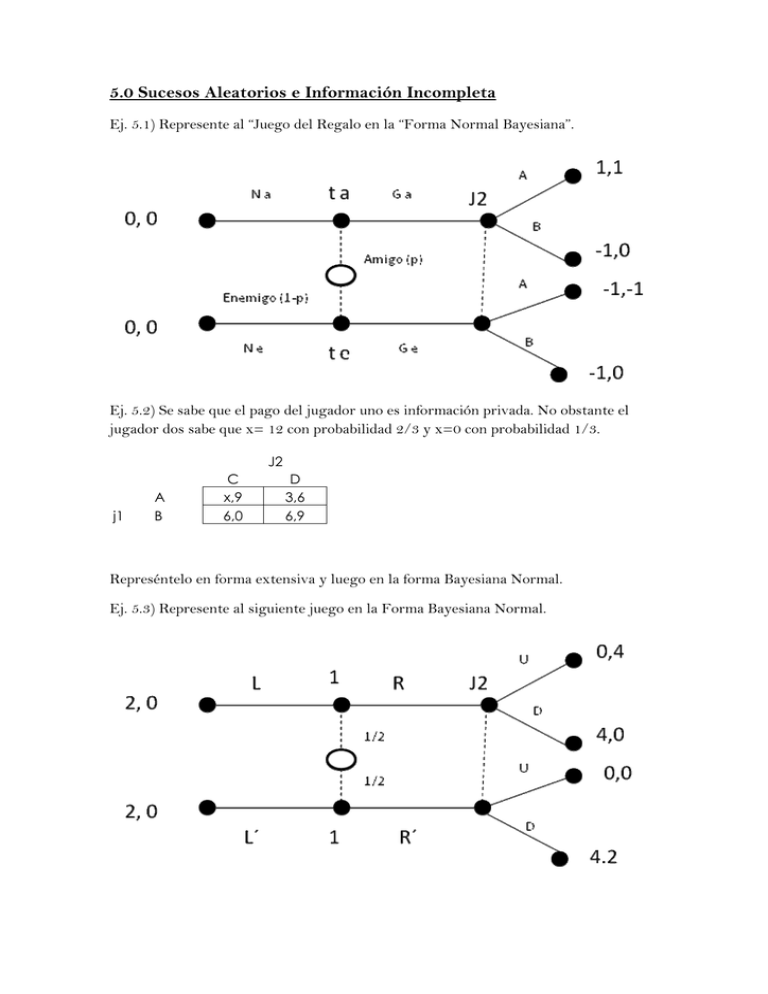
5.0 Sucesos Aleatorios e Información Incompleta Ej. 5.1) Represente al “Juego del Regalo en la “Forma Normal Bayesiana”. Ej. 5.2) Se sabe que el pago del jugador uno es información privada. No obstante el jugador dos sabe que x= 12 con probabilidad 2/3 y x=0 con probabilidad 1/3. J2 j1 A B C x,9 6,0 D 3,6 6,9 Represéntelo en forma extensiva y luego en la forma Bayesiana Normal. Ej. 5.3) Represente al siguiente juego en la Forma Bayesiana Normal. 6.0 Equilibrio Bayesiano de Nash Ej. 6.1) Encuentre el Equilibrio Bayesiano de Nash del ejercicio 5.2 Ej. 6.2) Encuentre el Equilibrio Bayesiano de Nash del ejercicio 5.3 Ej. 6.3 ) Considere el siguiente juego estático de información incompleta. La naturaleza determina que el tipo del jugador 1 será ( c), con c= 2 con probabilidad 2/3 y c)0 con probabilidad 1/3. El jugador 1 observa c (es decir que conoce su tipo) mientras que el jugador dos no observa c. Por lo tanto los jugadores realizan acciones en forma simultánea e independiente por las que reciben los pagos de acuerdo a la siguiente matriz: J2 j1 A B X 0,1 1,0 Y 1,0 c,1 a) Represéntelo en forma normal. b) Encuentre el Equilibrio Bayesiano de Nash. Ej. 6.4) Considere el siguiente juego: J2 j1 X Y Z V 6,0 0,0 5,1 J2 W 4,1 0,1 3,0 j1 X Y Z V 0,0 6,0 5,1 W 0,1 4,1 3,0 La Naturaleza selecciona A con probabilidad ½ y B con probabilidad ½. Si la Naturaleza selecciona A, entonces los jugadores interactúan de acuerdo a primera matriz, mientras que si seleccionan B, lo hacen de acuerdo a la segunda. Suponiendo que antes de que los jugadores elijan sus acciones, el jugador 1 observa la elección de la naturaleza (es decir, el jugador uno sabe en que matriz se está jugando). Mientras que el jugador 2 no observa la elección de la naturaleza. a) Represente al juego tanto en forma extensiva como en forma normal. b) Encuentre de forma iterativa el conjunto de estrategias racionalizables.











