TAXONOMÍA NUMÉRICA
Anuncio
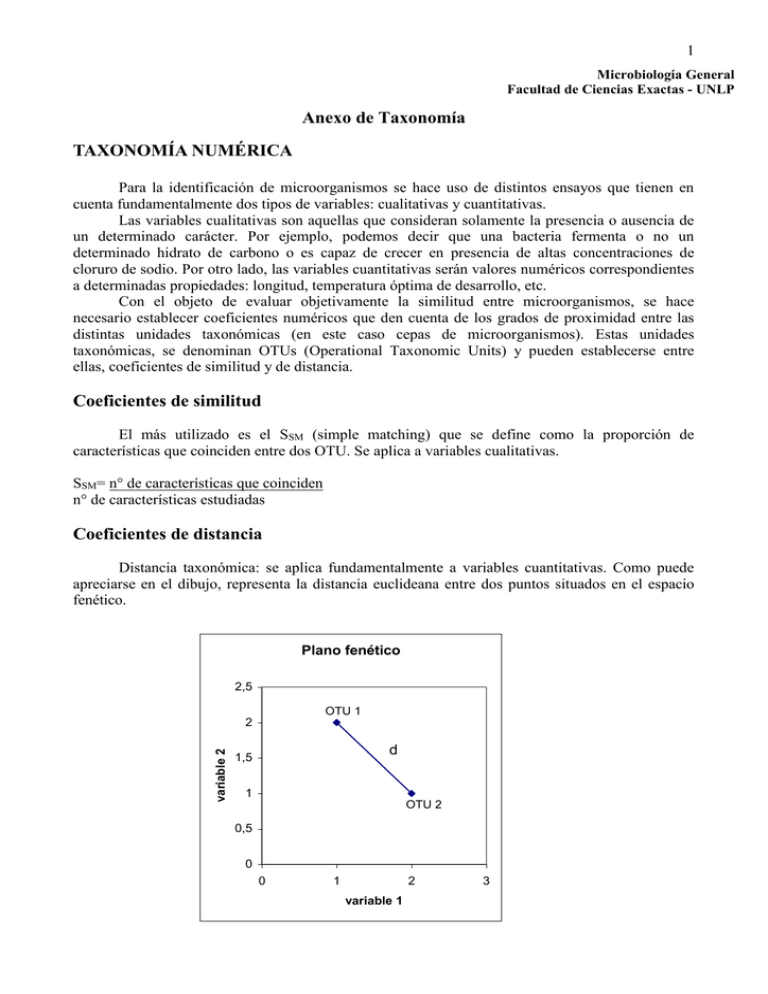
1 Microbiología General Facultad de Ciencias Exactas - UNLP Anexo de Taxonomía TAXONOMÍA NUMÉRICA Para la identificación de microorganismos se hace uso de distintos ensayos que tienen en cuenta fundamentalmente dos tipos de variables: cualitativas y cuantitativas. Las variables cualitativas son aquellas que consideran solamente la presencia o ausencia de un determinado carácter. Por ejemplo, podemos decir que una bacteria fermenta o no un determinado hidrato de carbono o es capaz de crecer en presencia de altas concentraciones de cloruro de sodio. Por otro lado, las variables cuantitativas serán valores numéricos correspondientes a determinadas propiedades: longitud, temperatura óptima de desarrollo, etc. Con el objeto de evaluar objetivamente la similitud entre microorganismos, se hace necesario establecer coeficientes numéricos que den cuenta de los grados de proximidad entre las distintas unidades taxonómicas (en este caso cepas de microorganismos). Estas unidades taxonómicas, se denominan OTUs (Operational Taxonomic Units) y pueden establecerse entre ellas, coeficientes de similitud y de distancia. Coeficientes de similitud El más utilizado es el SSM (simple matching) que se define como la proporción de características que coinciden entre dos OTU. Se aplica a variables cualitativas. SSM= n° de características que coinciden n° de características estudiadas Coeficientes de distancia Distancia taxonómica: se aplica fundamentalmente a variables cuantitativas. Como puede apreciarse en el dibujo, representa la distancia euclideana entre dos puntos situados en el espacio fenético. Plano fenético 2,5 OTU 1 variable 2 2 d 1,5 1 OTU 2 0,5 0 0 1 2 variable 1 3 2 La distancia entre OTU 1 y OTU 2 será : d=[(2-1)2 + (2-1)2]1/2 d 2 En el caso en que se estudien un gran número de variables, que es lo que ocurre en la práctica, ya no estaríamos hablando de un plano fenético sino de espacio fenético el cual tendrá tantas dimensiones como variables se estén considerando. La distancia taxonómica para este caso general será: d ( otu1 otu 2 ) 2 Donde los representan los valores de las variables correspondientes a cada cepa, para cada una de las características estudiadas. Para variables cualitativas, la distancia se define como d=[(1-SSM)]1/2, aunque también puede calcularse asignándole valores a las variables cualitativas (Ej. + 1 y - 2). REPRESENTACIÓN GRÁFICA DE LOS RESULTADOS: DENDROGRAMAS Para visualizar fácilmente las similitudes entre diferentes microorganismos, puede realizarse una representación gráfica. Obviamente, esto involucrará un análisis multifactorial debido al gran número de variables en estudio. A continuación se darán los pasos que se deben seguir en general para la construcción de un dendrograma. Una vez determinadas todas las características de los microorganismos en estudio, los datos se organizan en una matriz simétrica que se denomina matriz básica de datos. A continuación se da un ejemplo: Pruebas realizadas fermentación de glucosa sacarosa lactosa fructosa manosa arabinosa galactosa ramnosa celobiosa VP RM lecitinasa DNasa catalasa citocromo oxidasa reducción de NO3- cepas (OTUs) 1 2 3 4 + + + + + + + + + - + + + + + + + + + + + - + + + + + + + + + + - + + + + + + + 3 Posteriormente, se calculan los coeficientes de similitud entre todas las cepas y se disponen en la llamada matriz de similitud. Para el ejemplo dado será: OTU 1 2 3 4 1 100 50 69 25 2 3 4 100 43 62 100 19 100 Puede observarse que las OTU más relacionadas son la 1 y 3 con 69 % de similitud. Esto puede representarse gráficamente de la siguiente manera: 0 10 20 PORCENTAJE DE SIMILITUD 30 40 50 60 70 80 90 100 1 3 El próximo paso consiste en construir una nueva matriz en la que las OTUs 1 y 3 forman una sola OTU o cluster (1-3). A continuación pueden aplicarse tres métodos para la construcción de la nueva matriz: a) ligamiento máximo b) ligamiento mínimo c) ligamiento promedio Si se sigue el método del ligamiento máximo, la matriz se construye teniendo en cuenta los valores de máxima similitud. En el método del ligamiento mínimo por el contrario, la matriz se construye teniendo en cuenta los valores de mínima similitud. El método del ligamiento promedio es el que se utiliza habitualmente ya que otorga la menor distorsión respecto a la matriz original de datos. En este caso se la matriz se construye teniendo en cuenta el promedio entre las similitudes de las OTU involucradas. En el ejemplo será: (1-3) 2 (1-3) 4 (50 + 43)/2 = 46,5 (25 + 19)/2 = 22 La matriz resultante tendrá una dimensión menos. En este caso será: OTU 1-3 2 4 1-3 100 46,5 22 2 4 100 62 100 4 El próximo cluster resultará de la unión entre 2 y 4 ya que presentan el valor más alto de similitud dentro de la matriz (62%). 0 10 PORCENTAJE DE SIMILITUD 30 40 50 60 70 20 80 90 100 1 3 2 4 Siguiendo el mismo razonamiento, los grupos 1-3 y 2-4 se unirán en: (1-3) (2-4) (50+25+43+19)/4 = 34,25 Otra forma de calcular es: (1-3) 2 y (1-3) 4 (46,5 + 22) / 2 = 34,25 La nueva matriz de similitud según el método del ligamiento promedio será: OTU 1-3 2-4 1-3 100 34,25 2-4 100 Ahora puede construirse el dendrograma completo: 0 10 20 PORCENTAJE DE SIMILITUD 30 40 50 60 70 80 90 100 1 3 2 4 5 Como puede observarse, el dendrograma proporciona una representación gráfica que permite visualizar rápidamente las relaciones entre las distintas OTU. Obviamente, como en todo análisis multifactorial, algo de información se pierde durante el agrupamiento pero es de suma utilidad para resumir una gran cantidad de información. Debe tenerse en cuenta que la matriz de similitud involucra a veces cientos de características que resultarían imposible de analizar en conjunto. IDENTIFICACIÓN PROBABILÍSTICA Si se estudian las características de un gran número de cepas de una determinada especie bacteriana, se observará que para una prueba dada los resultados no serán siempre los mismos. Por ejemplo, si se estudia la producción de indol en 100 cepas de Escherichia coli (que se considera indol +), podría encontrarse que la reacción es positiva en 95 cepas. Esto no quiere decir que las cepas que no poseyeron la capacidad de producir indol no sean Escherichia coli sino que se apartan de las características generales de la especie. Es así que podríamos expresar las características de una determinada especie microbiana como la proporción (probabilidad) de que dé resultado positivo para una serie de caracteres estudiados. Las tablas de propiedades de las especies ya no serían una serie de resultados + ó - sino que estarían compuestas por los valores de las probabilidades. Supongamos que se dispone de las proporciones de resultados positivos para una serie de pruebas para cinco microorganismos de referencia: PRUEBA citrato movilidad VP oxidasa indol I 0.95 0.05 0.01 0.50 0.80 II 0.50 0.95 0.95 0.01 0.01 MICROORGANISMO III 0.95 0.95 0.01 0.05 0.99 IV 0.01 0.05 0.20 0.30 0.99 V 0.99 0.01 0.60 0.02 0.80 Si se quiere comparar un microorganismo desconocido con los de la tabla (base de datos) podrían estudiarse las características de este microorganismo realizando las mismas pruebas que las que figuran en la base de datos. Tomemos, a manera de ejemplo, que para el microorganismo problema se obtuvieron los siguientes resultados: citrato movilidad VP oxidasa indol + + + Teniendo en cuenta que las probabilidades de que una prueba de positivo es independiente de los demás resultados tendremos que, la probabilidad de que el microorganismo incógnita sea alguno de los microorganismos de referencia estará dada por: pI=0.95 x 0.95 x 0.01 x 0.50 x 0.80= 0.00361 pII=0.50 x 0.05 x 0.95 x 0.99 x 0.01= 0.0002351 pIII= 0.95 x 0.05 x 0.01 x 0.95 x 0.99= 0.0004467 pIV=0.01 x 0.95 x 0.20 x 0.70 x 0.99= 0.0013167 pV=0.99 x 0.99 x 0.60 x 0.98 x 0.80= 0.46 6 El microorganismo desconocido será más probablemente el microorganismo V. Si se quiere calcular la probabilidad de identificación, debe dividirse la probabilidad de cada uno de los microorganismos por la sumatoria de todas las probabilidades. En este caso será: p= 0.00361 + 0.0002351 + 0.0004467 + 0.0013167 + 0.46 = 0.4656085 y por lo tanto: PI= PII= PIII= PIV= PV= 0.00361/0.4656085 = 0.0077 0.0002351/0.4656085=0.00051 0.0004467/0.465685=0.0009592 0.0013167/0.465685=0.002827 0.46/0.465685= 0.9878 0.77 % 0.051 % 0.096 % 0.28 % 0.99 % Teniendo en cuenta los resultados del análisis efectuado, podemos decir que es más probable que el microorganismo desconocido sea el V y que la probabilidad de identificación es del 99 %. Este método se utiliza en los sistemas comerciales de identificación, en los cuales las bases de datos están constituidas por miles de cepas y se utilizan recursos informáticos para realizar los cálculos. BIBLIOGRAFÍA 1. Priest, F. and Austin, B. 1993. Modern bacterial taxonomy. Chapman & Hall. 2. Stanier, R. Y.; Ingraham, J. L.; Wheelis, M. L. y Painter, P. R. 1996. Editorial Reverté. 3. Crisci, J. V. y López Armengol, M. F. Introducción a la teoría y práctica de la taxonomía numérica. Secretaría General de la OEA, Washington, D. C.




